Transformer Based Neural Network Model of Magnetorheological Damper

August 3, 2025

Abstract

Magnetorheological (MR) dampers are a style of semi-active damper with growing applications in various fields. They utilize magnetorheological fluid, mineral oil with magnetically polarized particles, which can change its viscosity in response to a magnetic field. MR dampers exhibit complex nonlinear hysteresis behavior that make it difficult to accurately model. Previous studies analyzed the use of different parametric models and more recently, nonparametric models for MR damper simulation. However, a study has yet to evaluate the use of state-of-the-art transformer neural networks for this task.This study investigated the use of a transformer neural network to model the behavior of MR dampers. The research focused on development of the architecture of the transformer model and identification of the hyperparameters for the functionality of the model. The data that was used to train and test the model was sourced from the open source “Magnetorheological Damper test data for characterization and modeling” from the National Science Foundation. The model uses displacement of damper, acceleration of actuator, velocity of damper, and voltage to predict the damping force. The model was able to accurately predict the complex hysteresis behavior of the MR damper highly accurately, with an MSE (Mean Squared Error) of 0.0068. The transformer model was found to accurately derive known relationships between velocity, displacement, and damping force, further demonstrating the capability of the transformer network for modeling the behavior of MR dampers.

Introduction

Dampers are an essential component in various structures and systems that are designed and developed. They are commonly used to minimize unwanted vibrations in a system and are available in a wide range of designs from passive to active¹. Magnetorheological (MR) dampers are semi-active dampers with growing applications in a variety of fields such as earthquake resistant buildings and automobiles¹. Semi-active systems offer the adaptability of active systems while being more reliable and less energy dependent than comparable active systems¹.

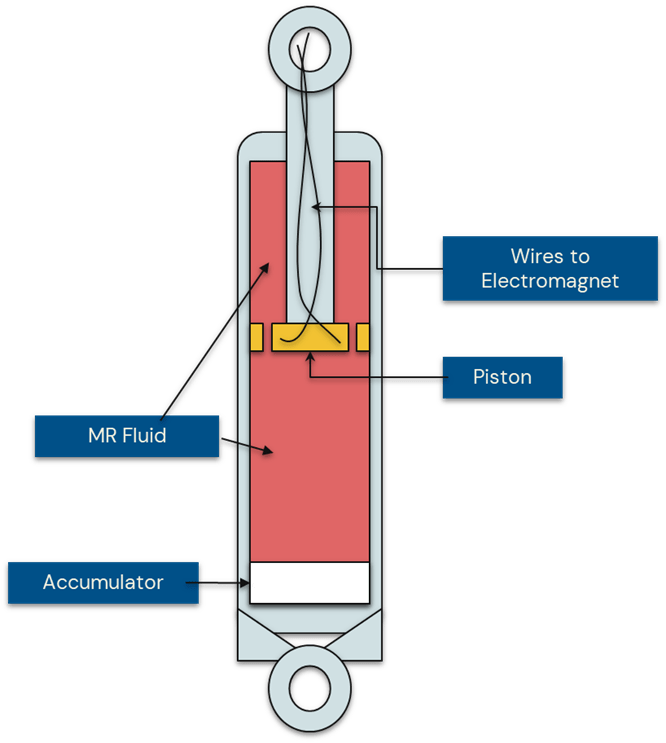
Figure 1: Simplified diagram of MR damper

Magnetorheological dampers use magnetorheological (MR) fluid, which changes its viscosity when exposed to varying magnetic fields. MR fluid used in the dampers is mineral oil with magnetically polarized particles, through which the damper piston travels. Variable voltage can be applied to the fluid, altering the internal MR fluid viscosity, thereby varying the available damping force. The dynamic adjustment of magnetic field and the resulting changes to the fluid viscosity create nonlinear behavior and historical dependencies. The complex nonlinear hysteresis behavior exhibited is difficult to model². Prior models can be classified into two types, namely parametric and nonparametric. Parametric models utilize physical properties and equations to model the non-linear behavior. Instead of relying on a fixed set of physical parameters, nonparametric models derive arbitrary relationships and patterns from the input data to predict the damping force.

Parametric models range from the simple Bingham viscoplastic model to the state of the art Spencer’s Modified Bouc-Wen model¹. The Modified Bouc-Wen model is the most accurate parametric model of an MR damper, where the damping force F is given by¹:

$F = \alpha z + c_0(\dot{x} - \dot{y}) + k_0(x - y) + k_1(x - x_0)$

$z$ represents the hysteresis component, which is the solution to the differential equation:

$\dot{z} = -\gamma |\dot{x} - \dot{y}| z |z|^{n-1} - \beta (\dot{x} - \dot{y}) |z|^n + A(\dot{x} - \dot{y})$

$\dot{x}$ and $x$ are used to represent velocity and displacement, respectively.

$\dot{y}$ is given by:

$\dot{y} = \frac{1}{c_0 + c_1}[\alpha z + c_0 \dot{x} + k_0(x - y)]$

y is the internal variable representing hysteresis. k₀ is used to represent the higher velocity stiffness control and k₁is the accumulator stiffness. c₀is the viscous damping coefficient observed at higher velocities.α, β, γ, and A are shaping parameters for the hysteresis component.

The Modified Bouc-Wen model¹ creates a highly accurate parametric model, however, it requires solutions to complex differential equations to obtain damping forces. Nonparametric models do not require solutions to differential equations. To date, different nonparametric models have been proposed, such as NARX³^,⁴, Multilayer Perceptrons (MLP)⁵, Deep Neural Networks (DNN)⁶, Extreme Learning Machines⁷, and Long Short-Term Memory Neural Networks (LSTM)⁸. Nonparametric models have been shown to be as effective at modeling the nonlinear hysteresis characteristics of MR dampers, particularly more recent models such as the LSTM model⁸.

In the field of nonparametric models, Bittanti et al. investigated the effectiveness of a NARX neural network model for an MR damper and compared it to the accuracy of traditional parametric models such as the Spencer Modified Bouc-Wen Model³^,⁹. In testing, the model was able to accurately predict damping force, outperforming the Modified Bouc-Wen model³.

Liu et al. also proposed the usage of a nonparametric NARX model with a single layer and a hidden size of 14 neurons⁴. This model had accurate predictions with an RMSE of 0.008 in best fitness and the study also evaluated the impacts of noise on the model⁴.

Duchanoy et al. proposed the usage of a deep neural network to model MR dampers using 8 inputs, 3 hidden layers utilizing ReLU activation functions, and 15 neurons per hidden layer⁶. The model performed with an R² accuracy of 0.9577⁶.

Saharuddin et al. investigated the use of an Extreme Learning Machine Algorithm for modeling MR dampers. Experiments were conducted using several different activation functions (hard limit, sigmoid, and sine)⁷. The best prediction accuracy using Extreme Learning Machines was in the trial utilizing the sine activation function with an RMSE(N) of 3.90⁷.

Delijani et al. utilized a series of six Multilayer Perceptron Neural Networks (MLP) to create a Sequential Neural Network (SNN) for prediction¹⁰. This model combines aspects of both parametric models and nonparametric models by using model parameters to represent physical properties⁵. 75% of the model’s predictions were found to have an absolute error less than 37.3 N¹⁰. The model’s predictions had an average R² of 0.9965, demonstrating an application of MLPs and SNNs in MR damper modeling⁵.

Hu et al. proposed an LSTM model which determined the relationships between displacement, velocity, and damping force⁸. The model’s minimum and maximum errors were 1.07% and 3.18% respectively⁸.

The Genetic Algorithm (GA) was recently proposed¹¹^,¹² as a solution for MR damper modeling. However, Jiang et al.’s MEA-BP network was found to outperform GA models on accuracy by 16.67%¹³.

Other model types like the Physics-Informed Neural Network (PINN)¹⁴, Supervised Neural Network¹⁵, and Enhanced Backpropagation Neural Network (BPNN)¹⁶ were also proposed. The PINN was found to demonstrate promising performance in estimating Bouc-Wen parameters but required further training in order to model hysteresis¹⁴. The Supervised Neural Network was specifically proposed for aircraft landing gear and was able to perform with comparable performance to existing hybrid models utilized for MR damper simulation¹⁷. The BPNN was found to improve MR damper control by 10-30% compared with existing control models¹⁸. These nonparametric models were able to model MR dampers with similar or superior accuracy to prior parametric, hybrid, and prior nonparametric models. Kowol et al. further investigated the use of nonparametric models to characterize MR fluid¹⁹. Experimentation showed that the neural network developed by Kowol et al. was in good agreement with experimental data¹⁹.

Research of the recent nonparametric models have shown that they are a viable alternative for modeling the MR dampers. Analysis of prior studies show that nonparametric models have the capacity to outperform the Spencer Modified Bouc-Wen model¹, however, prior models are limited by their architectures. The complex nonlinear hysteresis exhibited by MR dampers and a comparatively large number of inputs (e.g. damper velocity, damper piston displacement, voltage, internal fluid temperature, etc.)⁵^,⁴ creates complex long range dependencies. Without understanding the dependencies, the model has a high probability of error when applied to wide ranging research. Hence further research is needed to optimize a model that can make connections based on long range dependencies and handle the volume of inputs required to model an MR damper accurately.

At a high level, the objective of this study was to implement the state-of-the-art transformer neural network to model the behavior of an MR damper with comparable accuracy to prior parametric and nonparametric models. The intuition is that by leveraging the transformer based neural network architecture, a model can be developed which can demonstrate the accuracy required for future studies of dampers.

Development of such a model will aid in MR damper research to determine the factors that have the biggest impact on the damping force produced. These trained models should be ready to use in any architecture and design space exploration studies where MR dampers will be required. Design space exploration for products such as automobiles, bridges and prosthetics may benefit with the availability of the model.

To develop this model, data from “Magnetorheological Damper Test Data for Characterization and Modeling”²⁰ was used. This dataset is an open-source dataset published to provide data for training new models that can accurately model MR dampers²⁰. This dataset contains data for four major parameters (Displacement (D), Acceleration (A), Velocity (V), Voltage (Y)) and the resulting damping force based on the four parameters²⁰. The dataset includes data from 4 different experiments that were all conducted using a MR damper manufactured by the Lord Corporation, with a 3.8 cm cylinder diameter and a 30.5 cm stroke²⁰. Based on the data available, the model developed in this study incorporates only the four major parameters (D,A,V,Y) from the study.

Proposed Transformer Model Architecture

The transformer neural network proposed by Vaswani et al. in 2017 creates a foundation for a neural network with high extensibility and a self-attention mechanism which can be utilized to find long range dependencies like those present in the behavior of an MR damper²¹. Transformer neural networks have an attention mechanism which allows them to find long-range dependencies in the input data. They can also use attention to determine the relative importance of each part of input data. This is beneficial for modeling an MR damper where the function for damping force depends on multiple inputs. As described earlier, MR dampers demonstrate hysteresis behavior meaning that current damping force depends on historical states. The attention mechanism can be used as long term memory to find relationships between current and historical states. Transformers can also model complex nonlinear patterns like those seen between the input variables and damping force in MR dampers. Additionally, transformer models can handle large datasets efficiently and can easily support future inputs such as cylinder dimension, type of MR fluid, stroke length, etc. These characteristics will allow this model to provide high accuracy predictions despite the complex nonlinear hysteresis exhibited by MR dampers.

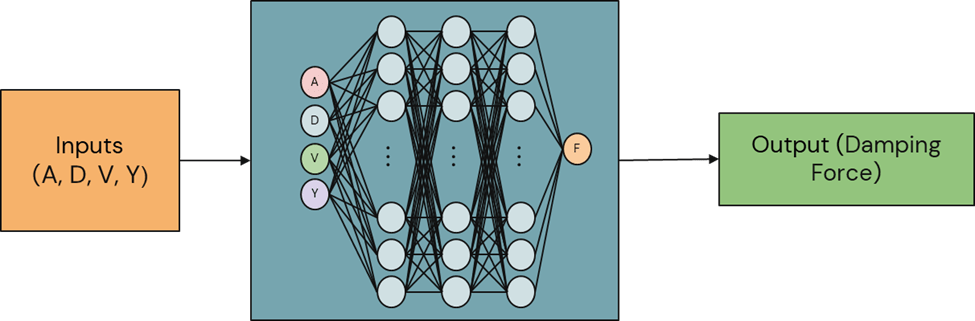
The proposed transformer model of an MR damper utilizes the 4 main inputs²⁰ which are fed through multiple encoder layers, with each layer focusing on different sections of the input, then through a feedforward neural network. The model incorporates multi-head attention²¹ as proposed by Vaswani et al. to capture different aspects of input relationships. Dropout was built into the model to prevent overfitting. Once the inputs passed through the multi-layer network, the predicted force was generated. The model was designed with both a forward and backward pass, with the criterion for accuracy being Mean Squared Error (MSE).

Architecture Description

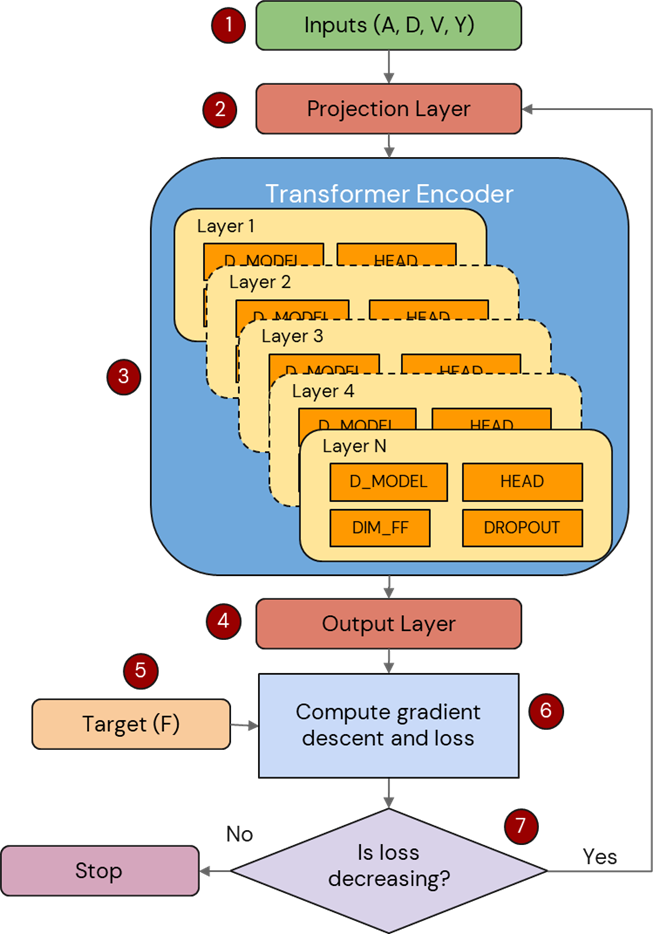
Figure 2: Proposed transformer model architecture

The main inputs Acceleration (A), Displacement (D), Velocity (V) and Voltage (Y) are scaled using RobustScaler and fed to the transformer model as shown in step 1 of Figure 2. The scaled values are then passed into the Projection Layer, which maps the input dimension to match the expected dimensions of the Transformer architecture. The proposed Transformer Encoder, as shown in step 3 of Figure 2 consists of: Multiple encoder layers, Multi-Head Attention, Feedforward Networks and Dropout. Multiple layers were used to allow each layer to focus on specific parts of the input. Multi-head attention is a feature of transformer neural networks²¹ that captures different aspects of the input relationships. Dropout helps in generalizing the model and preventing overfitting by randomly zeroing some of the elements of the input data with probability specified. This will ensure that the model is able to perform better on future datasets. After passing through the Encoder, the Output layer maps the features extracted by the Encoder into a single value, the predicted damping force, which is compared to the experimental damping forces²⁰ using gradient descent and Mean Squared Error (MSE). Training and validation loss are calculated using MSE for every epoch that the model is trained. The model ends training when it is determined that loss is not decreasing over a period of cycles. Predicting a single output value (F) based on input features (A, D, V, Y) is a machine learning regression problem. Hence a decoder layer is not required and only encoders are used in this design.

Hyper Parameter Tuning

Hyperparameters are parameters that influence the learning and accuracy of a model. Hyperparameters for the model are batch size, dropout, hidden size, number of layers, number of heads, and learning rate. Improperly tuned hyperparameters can greatly decrease prediction accuracy.

Hyperparameter	Initial Value	Optimized Value
d_model	320	1024
nhead	8	16
dim_feedforward	2816	1536
dropout	0.287801446876517	0.14481313775526408
num_layers	2	9
learning_rate	0.0002699320282307523	1.1447883968855328e-05
batch_size	243	117

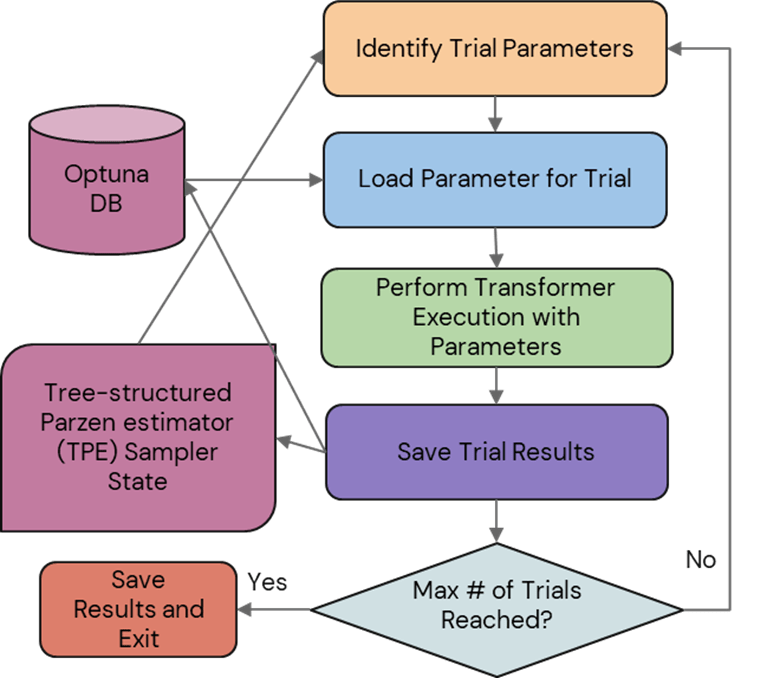
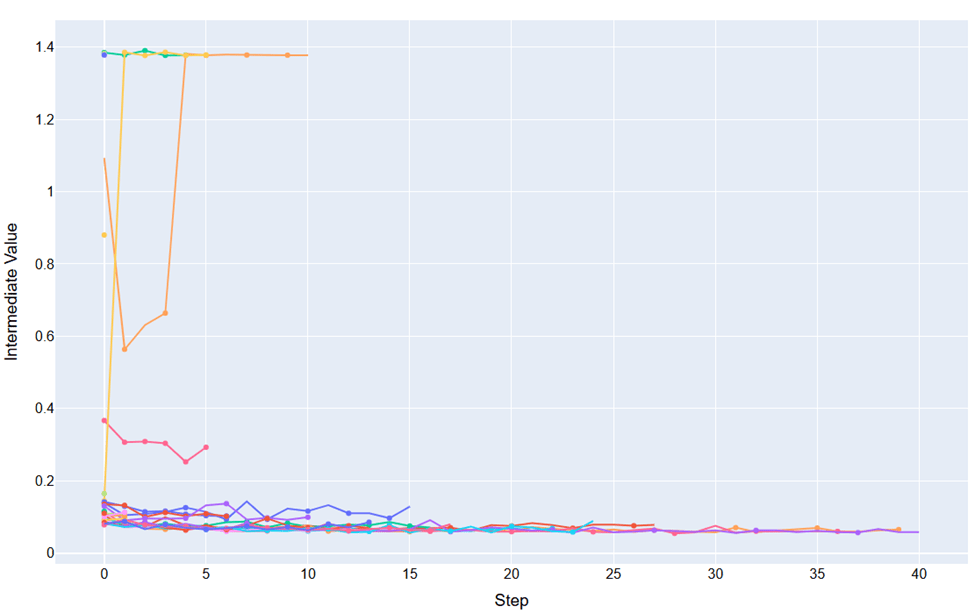
Table 1: Initial and Optimized Hyperparameter Values

To ensure that the hyperparameters were correctly optimized, Optuna Training Framework was utilized²². Optuna uses a Tree-structured Parzen Estimator (TPE) to optimize the hyperparameters to minimize prediction error²². The initial hyperparameter values were randomly chosen by the TPE. An algorithm to handle saving and restoring parameter optimization with DB storage was developed as shown in Figure 3. The initial and optimized hyperparameter values for each parameter are described in Table 1.

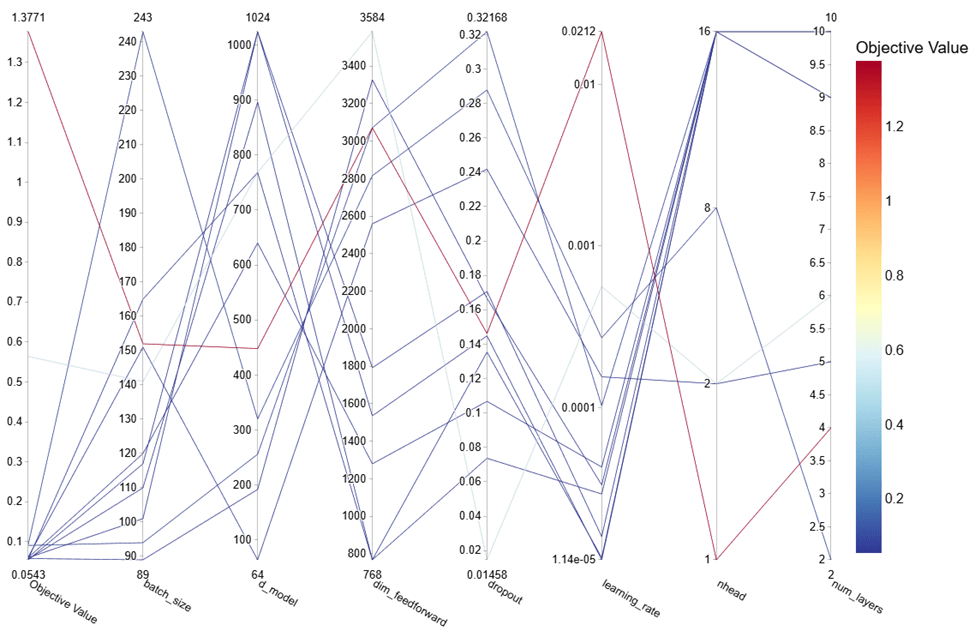
Figure 4: Parallel coordinate plot showing hyperparameters

The parallel coordinate plot in Figure 4 shows the relationship between the various hyperparameters and the resulting objective value, which in this figure represents the MSE.

Figure 5: Visual representation of pruning

A custom pruning algorithm to stop tuning was created and utilized for hyperparameter tuning. By analyzing the trend of the validation loss, the algorithm determined when a trial would be stopped. If the validation loss increased substantially or did not progress, the trial would be pruned, effectively reducing the amount of time that suboptimal parameters were analyzed. This algorithm will further optimize usage of compute resources when additional parameters are added in future studies. Pruned trials are visible in Figure 5 as lines that end before completion of all the steps.

Implementation

Data Preprocessing

The data used in this study was sourced from “Magnetorheological Damper Test Data for Characterization and Modeling”²⁰. The primary variables considered for this study were A (acceleration of actuator), D (displacement of damper piston), V (velocity of damper), Y (voltage), and F (damping force). These variables were experimentally measured by Dyke and Spencer before being published into an open source dataset²⁰. A linear variable differential transformer was used to measure the displacement of the damper piston and a load cell was used to measure the damping force²⁰. A servo valve was used to control the damper actuator and it produced different wave inputs for different experiments such as sine, triangle, step, and pseudo-random²⁰. These measurements were then compiled into the dataset.

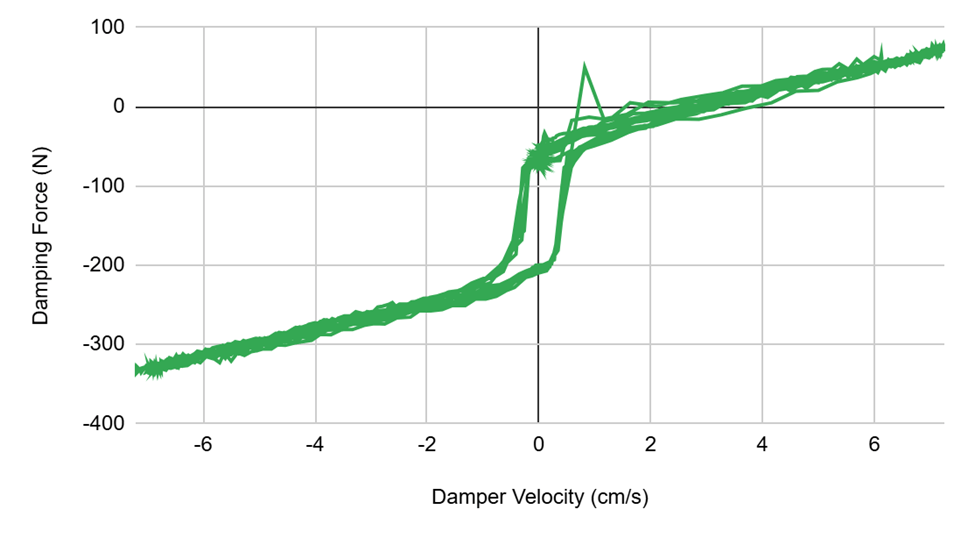
Figure 6: Nonlinear behavioral characteristics of MR dampers plotted using data from “Magnetorheological Damper Test Data for Characterization and Modeling”²³ correlating damper displacement and resulting damping force.

Figure 7: Nonlinear behavioral characteristics of MR dampers plotted using data from “Magnetorheological Damper Test Data for Characterization and Modeling”²³ correlating damper velocity and resulting damping force

Nonlinear behavioral characteristics of MR dampers as seen in the published dataset are shown in Figures 6 and 7. The published dataset had a total of 4 experiments and 66 trials, with each of the 66 csv files representing data from one experiment²³. 80% of the data was randomly selected for training, 20% for validation and testing. Within the 20% of files used for validation and testing, further splitting was done to divide the remaining data into separate validation and testing datasets. One randomly selected file was used for testing. Pandas python library was then used to read the CSV files selected for training and the data was appended to a training data dataframe. The features selected were A, D, V, and Y from the data and the target was F (damping force). The compiled training data was then shuffled. Both the features and target were scaled using RobustScaler²⁴.

The scaling values from RobustScaler²⁴ were then applied to the validation dataset. To ensure that the model was able to accurately make predictions of the complex nonlinear hysteresis behavior, windowing was used with a size of 10, stride of 1 and overlapping windows, allowing the model to see data in sequences. Through using sequences, the model is able to analyze the impacts of prior data points to more accurately represent hysteresis. During testing, the model was switched to inference mode, where it made predictions on damping force based on A, D, V, and Y in the test dataset.

Prior to training and validation, the input parameters (A, D, V, Y) and the target parameter (F) are scaled using RobustScaler²⁴. RobustScaler scales features using the median and the interquartile range (IQR), making it much more resilient to anomalies and outliers seen with data in MR dampers²⁴.

Transformer Model Implementation

A transformer model class was then developed, utilizing the four main inputs (A, D, V, Y), a projection layer, multiple encoder layers, a fully connected layer, and the output (Predicted damping force). A forward pass algorithm was built into the class.

A training function was then constructed, with MSE loss chosen as the criterion and Adam chosen as the optimizer²⁵. The function iterated through the training process for a given number of epochs. In each epoch, the function compared the model’s predicted damping force for a given set of inputs from the training data with the experimentally calculated damping force from the dataset. The weights were then adjusted to better fit patterns found in the training data.

The model additionally repeated a similar process every epoch using data from the validation dataset without adjusting weights. This was used to determine the accuracy of the model in predicting unseen data and ensuring that over- or underfitting was not present. Optuna Tuning Framework was used to optimize the hyperparameters of the model²². A patience algorithm was integrated into the validation process, where if validation loss did not decrease for a number of epochs beyond a certain patience, the model would end training. The early stopping was used for time optimization to ensure that unnecessary training with no improvement to accuracy was prevented. Once the model was completely trained, the model and the files for scalers were saved.

The test data was then passed through the model which was set to inference mode. The predictions of the model were then compared with the experimentally obtained values of damping force from the open-source dataset to evaluate the performance of the model.

Results from Training and Validation

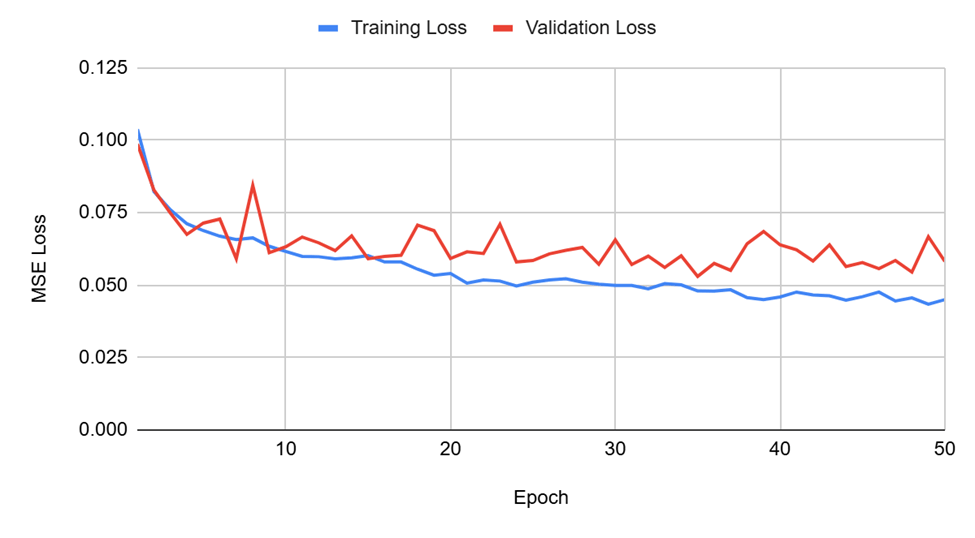
MSE (Mean Squared Error) was used to evaluate the accuracy of the model. With a run of 50 epochs, the lowest recorded validation loss was on epoch 35, with a training loss of 0.0480 and a validation loss of 0.0530. The model, with its weights from epoch 35, was saved and set to inference mode, where it recorded a test loss of 0.0068. The accuracy of the model was limited by access to computing resources. Further training would have likely led to greater accuracy.

Figure 9: Progression of training and validation loss

Discussion

The results of experimentation show that a transformer neural network accomplished the engineering goal of this study. From the predictions of the model, it can be seen that the proposed model is capable of making accurate predictions of the complex nonlinear hysteresis of MR dampers, with a prediction loss of 0.0068 MSE, showing that the transformer model has high accuracy on the test dataset. Relative comparisons across other nonparametric models is infeasible without access to prior models or the datasets used for studies. Nonuniform error reporting techniques also makes the comparison difficult.

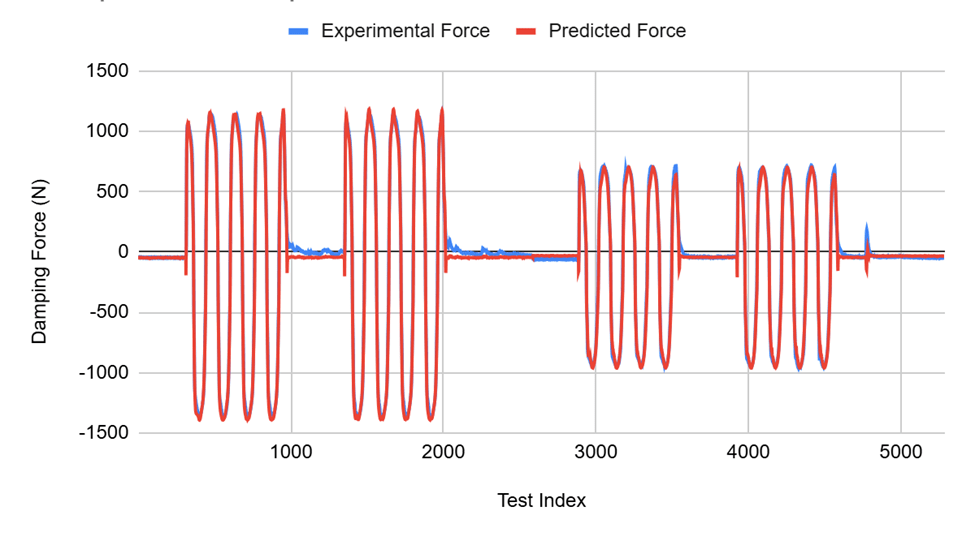
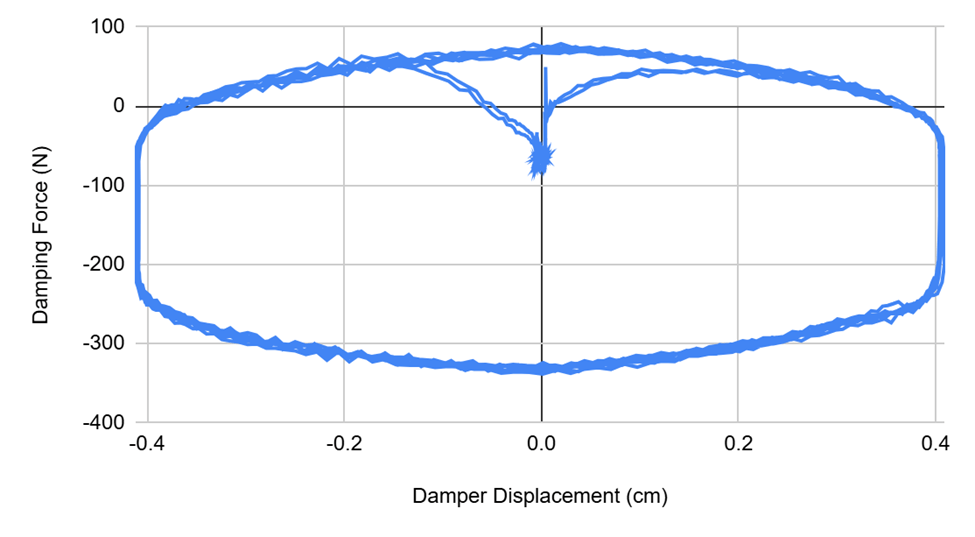
Figure 10: Comparison of model predictions and experimental force²³ per test index

The graph shows a strong correlation between the predictions of the model and experimentally obtained values²³ for damping force. The model was able to accurately predict experimental values for both positive and negative forces. The graphs also show that the model was able to accurately discover the relationship between the inputs (piston displacement, piston velocity) and damping force despite not being trained using physical properties or equations. Deviations in the graph can be attributed to the MSE loss that was observed.

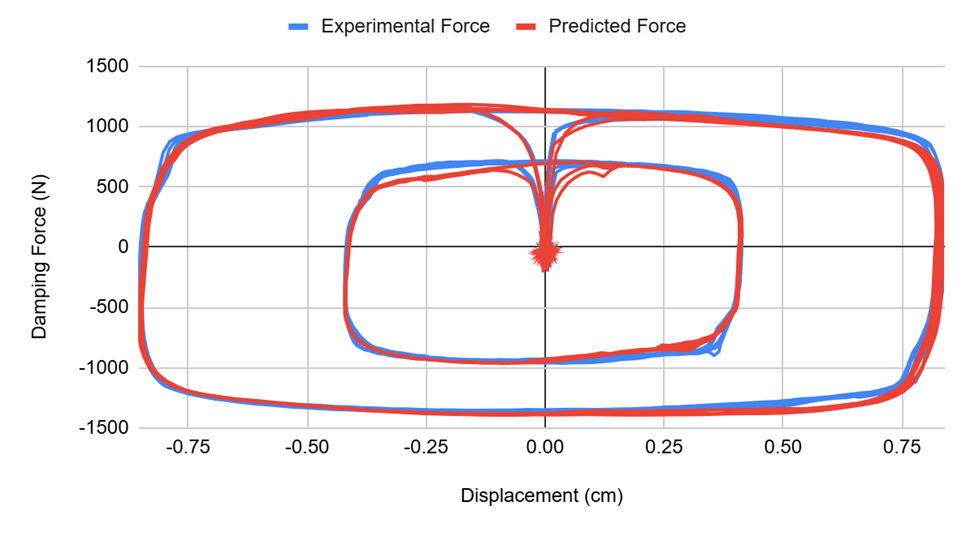
Figure 11: Comparison of model predictions and experimental force²³ with respect to displacement

Figure 11 shows that the model was able to derive the “loop” pattern noted by Spencer et al.¹ in their study between displacement and damping force.

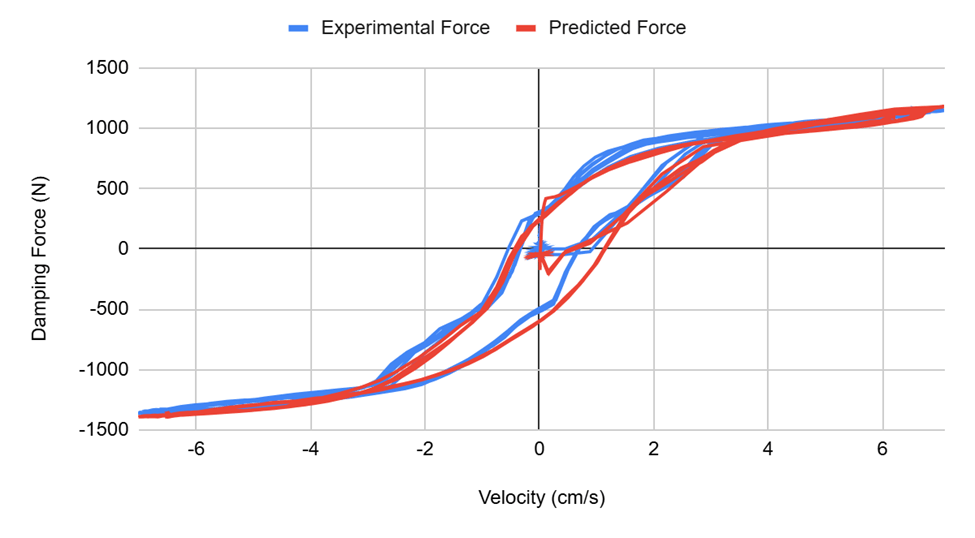
Figure 12: Comparison of model predictions and experimental force²³ with respect to velocity

Spencer¹ study analyzed the correlation found in MR dampers between velocity and damping force and found a near linear force-velocity at higher velocities that became increasingly more non-linear at lower velocities. The study¹ cited that this behavior will be “sought after” in MR damper models. In Figure 12, it can be seen that the transformer model was able to accurately derive this relationship as described by Spencer et al,¹ showing that transformer models are viable for modeling the hysteresis behavior of MR dampers.

Conclusion

This study investigated the use of a transformer-based neural network model for modeling magnetorheological (MR) dampers. The study was conducted using data from the National Science Foundation. After training, the model was evaluated; during evaluation the model performed with an error of 0.0068 MSE, showing that the model was able to accurately model an MR damper. Additionally, the model derived the key relationships between velocity or displacement and damping force described in Spencer et al.’s 1997 study. The accuracy of the transformer model will enable study of MR dampers. The proposed model has the potential to improve design space exploration of MR dampers in fields from prosthetics to automobiles. This study was limited by open-source data availability and further research needs to be conducted to include additional factors such as stroke length to optimize the model further. Additionally, the dataset used to train the model only contained data for one specific style of MR damper manufactured by the Lord Corporation. To make the model more representative of all MR dampers, further training and data availability is required. Additionally, comparisons should be made using other existing parametric and nonparametric models on identical datasets to determine the relative accuracy of each model.

References

B. F. Spencer Jr., S. J. Dyke, M. K. Sain, J. D. Carlson. Phenomenological Model for Magnetorheological Dampers. Journal of Engineering Mechanics. 123(3), 230–238. https://doi.org/10.1061/(asce)0733-9399(1997)123:3(230) (1997). [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
B. Sapinski, J. Filus. Analysis of Parametric Models of MR Linear Damper. Journal of Theoretical and Applied Mechanics. 41, 215-240 (1991). [↩]
S. Bittanti, S. M. Savaresi, M. Montiglio. Neural-Network Model Of A Magneto-Rheological Damper. https://doi.org/10.1016/S1474-6670(17)30850-9 (2004). [↩] [↩] [↩]
Q. Liu, W. Chen, H. Hu, Q. Zhu, Z. Xie. An Optimal NARX Neural Network Identification Model for a Magnetorheological Damper With Force-Distortion Behavior. Frontiers in Materials. https://doi.org/10.3389/fmats.2020.00010 (2020). [↩] [↩] [↩] [↩]
Y. M. Delijani, S. Cheng, F. Gherib. Sequential Neural Network Model for the Identification of Magnetorheological Damper Parameters. Smart Materials and Structures. https://doi.org/10.1088/1361-665X/ad0f36 (2024). [↩] [↩] [↩] [↩]
C. A. Duchanoy, M. A. Moreno-Armendariz, J. C. Moreno-Torres, C. A. Cruz-Villar. A Deep Neural Network Based Model for a Kind of Magnetorheological Dampers. Sensors. https://doi.org/10.3390/s19061333 (2019). [↩] [↩] [↩]
K. D. Saharuddin, M. H. M. Ariff, K. Mohmad, I. Bahiuddin, Ubaidillah, S. A. Mazlan, N. Nazmi, A. Y. A. Fatah. Prediction Model of Magnetorheological (MR) Fluid Damper Hysteresis Loop using Extreme Learning Machine Algorithm. Open Engineering. https://doi.org/10.1515/eng-2021-0053 (2021). [↩] [↩] [↩]
Y. Hu, X. Zhu, Y. Wang. Research on the Kinematics Model of MR Dampers Based on LSTM Neural Network. 2024 3rd International Conference on Service Robotics (ICoSR). https://ieeexplore.ieee.org/abstract/document/10795372 (2024). [↩] [↩] [↩] [↩]
B. F. Spencer Jr., S. J. Dyke, M. K. Sain, J. D. Carlson. Phenomenological Model for Magnetorheological Dampers. Journal of Engineering Mechanics. 123(3), 230–238. https://doi.org/10.1061/(asce)0733-9399(1997)123:3(230) (1997). [↩]
Y. M. Delijani, S. Cheng, F. Gherib. Sequential Neural Network Model for the Identification of Magnetorheological Damper Parameters. Smart Materials and Structures. https://doi.org/10.1088/1361-665X/ad0f36 (2024). [↩] [↩]
T. Zhang, Z. Ren. Optimization of MR damper model based on improved genetic neural network algorithm. ISCER. https://dl.acm.org/doi/10.1145/3679409.3679415 (2024). [↩]
W. Gong, P. Tan, S. Xiong, D. Zhu. Experimental and numerical study of the forward and inverse models of an MR gel damper using a GA-optimized neural network. Journal of Intelligent Material Systems and Structures. https://journals.sagepub.com/doi/abs/10.1177/1045389X231168774 (2023). [↩]
M. Jiang, X. Rui, F. Yang, P. Wang, H. Li, W. Wang. Non-parametric modeling of magnetorheological damper based on MEA-BP neural network. Journal of Vibration and Control. [↩]
Y. Wu, B. Sicard, P. Kosierb, S. A. Gadsden. Parameter Identification in Magnetorheological Dampers via Physics-Informed Neural Networks. Proceedings of IEMTRONICS 2024. https://doi.org/10.1007/978-981-97-4780-1_13 (2024). [↩] [↩]
Q-V. Luong, B-H. Jo, J-H. Hwang, D-S. Jang. A Supervised Neural Network Control for Magnetorheological Damper in an Aircraft Landing Gear. MDPI Structural Vibration: Analysis, Control, Experiment, and Applications II. https://doi.org/10.3390/app12010400 (2022). [↩]
M. Wang, H. Pang, J. Luo, M. Liu. On an enhanced back propagation neural network control of vehicle semi-active suspension with a magnetorheological damper. Transactions of the Institute of Measurement and Control. https://doi.org/10.1177/01423312221118224 (2022). [↩]
Q-V. Luong, B-H. Jo, J-H. Hwang, D-S. Jang. A Supervised Neural Network Control for Magnetorheological Damper in an Aircraft Landing Gear. MDPI Structural Vibration: Analysis, Control, Experiment, and Applications II. https://doi.org/10.3390/app12010400 (2022). [↩]
M. Wang, H. Pang, J. Luo, M. Liu. On an enhanced back propagation neural network control of vehicle semi-active suspension with a magnetorheological damper. Transactions of the Institute of Measurement and Control. https://doi.org/10.1177/01423312221118224 (2022). [↩]
P. Kowol, G. Lo Sciuto, R. Brociek, G. Capizzi. Magnetic Characterization of MR Fluid by Means of Neural Networks. MDPI Computer Science & Engineering. https://doi.org/10.3390/electronics13091723 (2024). [↩] [↩]
S. J. Dyke, B. F. Spencer. Magnetorheological Damper Test Data for Characterization and Modeling [Data set]. NSF NHERI DesignSafe. https://www.designsafe-ci.org/data/browser/public/nees.public/NEES-2012-1158 (2012). [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomes, L. Kaiser, I. Polosukhin. Attention Is All You Need. https://arxiv.org/pdf/1706.03762 (2017). [↩] [↩] [↩]
T. Akiba, S. Sano, T. Yanase, T. Ohta, M. Koyama. Optuna: A Next-generation Hyperparameter Optimization Framework. https://optuna.org/#paper (2019). [↩] [↩] [↩]
S. J. Dyke, B. F. Spencer. Magnetorheological Damper Test Data for Characterization and Modeling [Data set]. NSF NHERI DesignSafe. https://www.designsafe-ci.org/data/browser/public/nees.public/NEES-2012-1158 (2012). [↩] [↩] [↩] [↩] [↩] [↩] [↩]
A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, S. Chintala. PyTorch: An Imperative Style, High-Performance Deep Learning Library. PyTorch. https://arxiv.org/pdf/1912.01703 (2019). [↩] [↩] [↩] [↩]
D. Kingma, J. Ba. Adam: A Method for Stochastic Optimization. 3rd International Conference for Learning Representations. https://arxiv.org/abs/1412.6980 (2014). [↩]

Transformer Based Neural Network Model of Magnetorheological Damper

Abstract