Investigating Delta Encoding with Error Control for Scientific Data Reduction

Abstract

As scientific computing reaches new heights with the next generation of processors, such as graphics processing units (GPUs), scientific discovery can operate at a fidelity previously unattainable. The data generated by scientific applications has grown immensely, resulting in significant storage overhead for knowledge discovery. In recent years, scientific data reduction has gained renewed attention due to the development of new algorithms for compressing  floating-point data. This paper develops a delta encoding algorithm that guarantees bounded error after decompression, and evaluates its performance in conjunction with run-length encoding. In the literature, there were no comprehensive performance results on delta encoding for scientific data, and this paper aims to fill this gap. As shown in this work, delta encoding with run-length encoding outperforms state-of-the-art in some scenarios and therefore needs to be adopted into compression tools. The methodology includes calculating the difference between data points delta based on the reconstructed value, instead of the actual value, of the previous data point. This way, after decompression, the error will not propagate throughout the datum. We evaluated four real datasets and compared the compression performance, including both compression ratios and throughput of delta encoding against the scenario where data is directly quantized. The results show that the error after reconstruction can be effectively bounded. Overall, delta encoding is shown to deliver performance improvements in some scenarios as compared to the case where data is directly quantized as well as state-of-the-art, motivating future research into automatic algorithm selection.

Keywords: Big data, data compression, scientific applications

Introduction

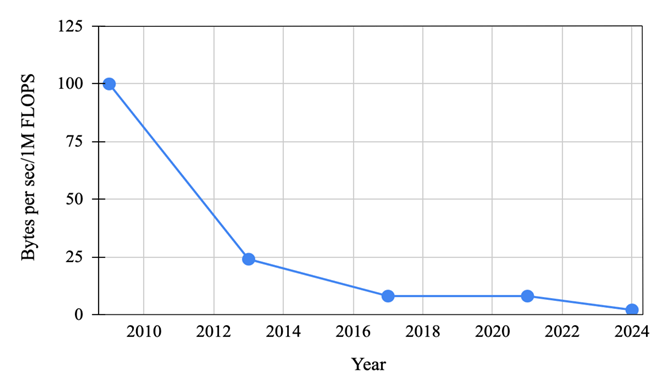
As scientific computing advances to the next level through state-of-the-art processors, such as graphics processing units (GPUs), scientific discovery can run with a fidelity that was previously unattainable. The data generated from scientific applications has become increasingly large, which creates high storage overheads for knowledge discovery. Figure 1 below illustrates the trend of storage throughput versus computing speed in 1 million floating-point operations per second (FLOPS) for supercomputers at Oak Ridge National Laboratory over the past 15 years, where the gap between computing and storage has continued to widen.¹ As a result, scientists may need hours, days, and even weeks to retrieve and analyze data. The scientific computing community has proposed numerous methods at various computer system layers to accelerate the knowledge discovery process. For example, at the storage system layer, scalable and high-performance storage devices, such as solid-state drives (SSDs) and non-volatile memory (NVM), have been developed to accelerate the read and write speeds of scientific applications. At the data management layer, researchers have developed in-situ processing where data are analyzed while they are in memory thereby minimizing the need for expensive input/output (I/O) operations to persistent storage systems.

In recent years, scientific data reduction has resurfaced due to the development of new lossy algorithms for floating-point data compression, and it has become increasingly indispensable in scientific workflows. In general, floating-point data compression consists of lossless and lossy compression. For the former (e.g., Zstd², Zlib³ after decompression, the data is identical to the original data at the byte level. Such a stringent requirement often leads to lower compression, and the resulting overhead of data retrieval can still be high, given that compression is not free and will involve substantial computational overhead itself. As such, lossless compression is often used in scenarios where the loss of accuracy is not permitted, such as for checkpointing. For the latter, information will be lost during data reduction, and therefore, the decompressed data will not be identical to the original data. The key benefit of lossy compression is that the compression ratios, defined as the ratio of the input and output data size, will be significantly higher than lossless compression so that the amount of data to be placed onto or retrieved from computer storage systems is less than the case without compression. Compared to state-of-the-art lossy compressors, including SZ⁴, Compressed Floating-Point and Integer Arrays (ZFP)⁵, and MultiGrid Adaptive Reduction of Data (MGARD)⁶ (see the Literature Review section for more details), this paper aims to explore a unique combination of delta encoding and run-length encoding, which was not implemented in existing compressors, and evaluate its performance. As shown in the results, this work achieves performance improvements in certain scenarios over the state-of-the-art, indicating further potential for performance gains in compression tools. For lossy compression, error control is often employed to ensure that the deviation of the decompressed data from the original data is small enough to control the loss of information. There are various ways to enforce error control, such as absolute error, relative error, and L-infinity error. For a particular data point with its value of d, assume its value is d’ after decompression. For the absolute error bound, denoted as e, . For the relative error bound,
. For the L-infinity absolute error, |d-d’|max ≤ e, while for the L-infinity relative error,.

This paper implements delta encoding, which is commonly used in signal processing to manage data that do not change substantially across adjacent time steps. The quantized data will be further compressed using run-length encoding to reduce its storage footprint. In particular, this work developed a key technique for error control where the delta is calculated based on the predicted value, rather than the original data value as commonly used in signal processing. This study evaluated the performance of delta encoding utilizing a set of real scientific floating-point data and compared it with the case where data is directly quantized without using delta encoding. The significance of this research lies in the fact that, with error control, the delta encoding used in conjunction with quantization can now limit the error, ensuring that the outcomes of scientific data analysis do not deviate substantially from the ground truth, while significantly accelerating the process. For example, in the fusion simulation, scientists need to make near real-time decisions to avoid instabilities that develop in the system. Without error control, the fusion instabilities captured in the data may be discarded by the analysis routine, which can result in significant repair costs for the fusion device. This paper focuses on the widely used lossless compression algorithm, run-length encoding (RLE), and basic uniform quantization.

Literature Review

State-of-the-art lossy compressors include SZ, ZFP, and MGARD. In particular, SZ employs a multi-algorithm prediction and regression approach for curve fitting. For those data points that can be curve-fitted, quantization followed by Huffman encoding will be performed further for entropy encoding. Meanwhile, ZFP uses an orthogonal transformation to decorrelate data points within a block and uses embedded coding to compress each bitplane. MGARD converts data to multi-level coefficients through interpolation and an L2 projection.

Methods

Our study implements a scientific data compression pipeline using delta encoding, followed by quantization and run-length encoding. The general idea of delta encoding is to capture the change of adjacent data points, rather than the value of data itself. During the compression process, the quantization step is lossy making error control necessary to ensure the error is within a reasonable threshold. The decompression process is opposite to compression and begins with run-length decoding, followed by dequantization and delta decoding. In what follows, we further describe the algorithms of each step.

Quantization

Quantization is a lossy compression technique where continuous values are assigned to discrete buckets. The reason for using quantization is that data points that are close to each other can be mapped into the same bucket, allowing the data to be better compressed using lossless compression. Although quantization retains the overall characteristics of data, it introduces errors to the data and, therefore, needs to be done carefully. For uniform quantization, where each bucket has an equal interval, the error is half the size of a bucket. In this paper, based on the error (denoted as error) prescribed by the user, the size of a bucket is 2*error. Further, the quantization buckets are arranged as follows. The first bucket (bucket 0) is allocated to the range of [-error, error], and the second bucket (bucket 1) is allocated to the range of [error, 3*error], and so on. In general, bucket i has a range of [i*error, (i+2)error].

Delta Encoding

Delta encoding is a method of representing a sequence of values as the differences between consecutive data points. The intuition behind delta encoding for compression is that many scientific datasets have local smoothness. By using delta encoding, we can further expose the inherent redundancy in data and achieve higher compression ratios.

Algorithm 1 shows the pseudo-code for delta encoding. The data to be compressed is denoted as D, and the user-prescribed error bound is denoted as error. The algorithm begins by allocating memory space using the malloc() function. The variable last, initialized to 0, represents the value of the previous data point. Lines 3 to 13 are a loop that goes through all data points in D and generates the compressed value. In particular, for a data point d[i], the delta is calculated in Line 5 by subtracting last from the current data point. Lines 6 to 10 further quantize the delta. This is done by first obtaining the sign of the delta; a negative value will result in a negative bucket number. The bucket number that the delta falls in is calculated in Line 10 as sign*(abs(delta)+error)/(2*error), where abs(delta) represents the absolute value of delta. Our quantization is a simple uniform quantization where the range of the bucket 0 is [-error, error] and the range of the second bucket is [error, 2*error], and so on. As such, the term abs(delta)+error calculates the distance between the value of delta and the lower end of bucket 0. Then, the bucket number can be obtained by dividing the distance by the size of a bucket.

To control accuracy and satisfy the prescribed error, the delta calculated is based on the reconstructed value rather than the true value of the previous data point.

Algorithm 2 shows the pseudo-code for delta decoding. Similar to Algorithm 1, it starts by allocating memory space at Line 1. The decoding for a data point d[i] is done in Lines 5 to 7. In particular, we retrieve the bucket number from the quantized data x[i], and the reconstructed value D[i] is calculated by computing the delta, which is the midpoint of the associated bucket (bucket * 2 * error), and add it to the previous reconstructed value (last).

In Fig. 2, we show an example of error control we implemented in the delta encoding. Assume we compress four data points: 10, 170, 760, and 920, with an error tolerance of 100. As a result, the size of a bucket in quantization is set to 200.  Without error control, the delta encoding will transform the data to 10, 160, 590, and 160. These three delta values will be next quantized into buckets 0, 0, 2, and 0. During reconstruction, the deltas will be decoded to the mid-value of each bucket, which will be 100, 100, 500, and 100. After applying for delta decoding, the reconstructed data will be 100, 200, 700, and 800. The first three data points are within the error tolerance, whereas the absolute error of the fourth data point, which is 120, exceeds the error tolerance of 100.

In this paper, we developed an error control technique for delta encoding. In contrast to the case without error control, the deltas calculated will be using the reconstructed data as a reference. For example, the second delta is calculated as 170-100=70, rather than 170-10=160. As such, the error from the previous iteration will not be propagated further, preventing the error from compounding. In Fig. 2, the delta after error control is 10, 170-100=70, 760-200=560, and 920-700=220. The delta is further mapped to buckets 0, 0, 2, and 1. During decompression, the reconstructed delta is 100, 100, 500, and 300, and after delta decoding, the data is 100, 200, 700, and 1000. All data points are now within the error bound. As a result, the error will not be propagated to the subsequent data points and will not exceed the prescribed error bound.

Run-Length Encoding (RLE)

RLE is a lossless compression algorithm that compresses sequences of repeated values by representing them as pairs of the value and its frequency. For example, the sequence of symbols [A, A, A, B, B] is encoded as [A, 3, B, 2], indicating that the value A appears three times and B appears twice. By doing this, the storage footprint of highly repeated symbols can be reduced. In this paper, to ensure the repetition of symbols in data, we perform either quantization directly or delta encoding followed by quantization so that data points near each other can be converted into the same bucket, making them suitable for RLE. Algorithms 3 and 4 provide further details for encoding and decoding of RLE, respectively. For encoding, Lines 5 to 7 calculate the length (count) of a run in the data. After that, the encoded symbol and its length will be recorded at x[x_index] and x[x_index+1], respectively.

Experimental Setup

This work was conducted on an Apple Mac computer. The processor is Apple M3 with 16 GB of DDR3 DRAM. The disk space is 1 TB. The code was written using C, and the compiler we used was GCC. The code is publicly available on GitHub⁷. We measured the compression performance in terms of compression ratios and throughput. We tested out the compression algorithms using four datasets from SDRBench. They are all single-precision floating-point data and are described below.

• Exaalt: This data is produced by a molecular dynamic simulation developed by Los Alamos National Laboratory. In particular, we tested the vx.dat2 file, which is the velocity field in the X-dimension. This is 1D data with 2,869,440 data points.
• NYX: This data is produced by an adaptive mesh N-body cosmological simulation and has 6 fields of 3D data with dimensions of 512 x 512 x 512. In particular, we tested the field of baryon_density.f32.
• QMCPACK: This data is produced by a many-body ab initio quantum Monte Carlo simulation. It has 1 field and 288 orbitals of 3D data, with dimensions of 69 x 69 x 115.
• Hurricane ISABEL: This is produced by a weather simulation and consists of 13 fields. Each field is 3D, with dimensions of 100 x 500 x 500. In particular, we tested the field of Vf48.bin.f32.

The preprocessing steps of the data include the following: 1) The datasets are downloaded from the SDR benchmark website (https://sdrbench.github.io/) and stored on the local disk. 2) A C/C++ function called float * readdata(char * fname, int * num_elements) is used to read the binary data from each dataset. Within this function, the C/C++ function fread() is used to retrieve data from the file.

Results

Dataset	Delta encoding + quantization + RLE	SZ	ZFP
EXAALT	0.6	11.94	4.21
NYX	645277.562500	426426.46	128
QMCPACK	34.264912	414.01	12.9
Hurricane	14.182482	199.69	6.67

Dataset	Delta encoding + quantization + RLE	SZ	ZFP
EXAALT	121.977959	119	171
NYX	309.158966	148.2	2337.9
QMCPACK	184.927307	141.8	784
Hurricane	181.749451	145.4	454.1

Compression routine	Compute time (secs)	Memory usage (GB)
Delta encoding	2.65	1
Quantization	0.1	1
RLE	0.23	1.5

Decompression routine	Compute time (secs)	Memory usage (GB)
Delta decoding	0.35	1
Dequantization	0.1	1
RLD	0.29	1.5

Discussion

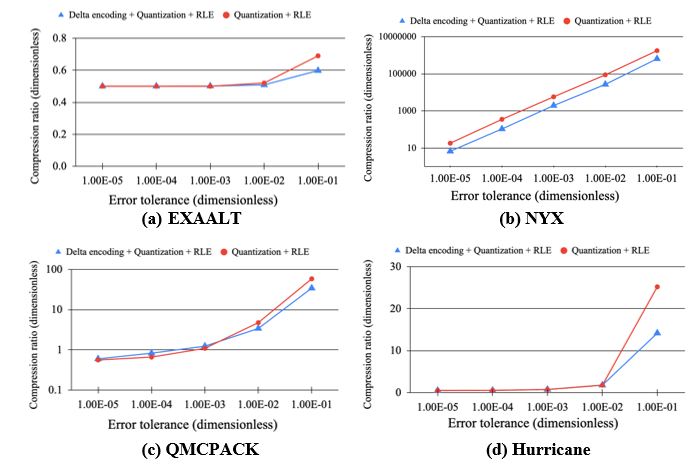
In Fig. 4, the impact of delta encoding about the compression ratio for four real datasets, EXAALT, NYX, QMCPACK, and Hurricane, is evaluated. In particular, the performance of the following two cases was tested: Case 1: We directly quantize the data based on the prescribed error and further compress it with run-length encoding (RLE); Case 2: We apply delta encoding to preprocess the data, and the resulting deltas are then further quantized and compressed. The relative error varies from 1E-5 to 1E-01 to test the compression sensitivity to error bounds.

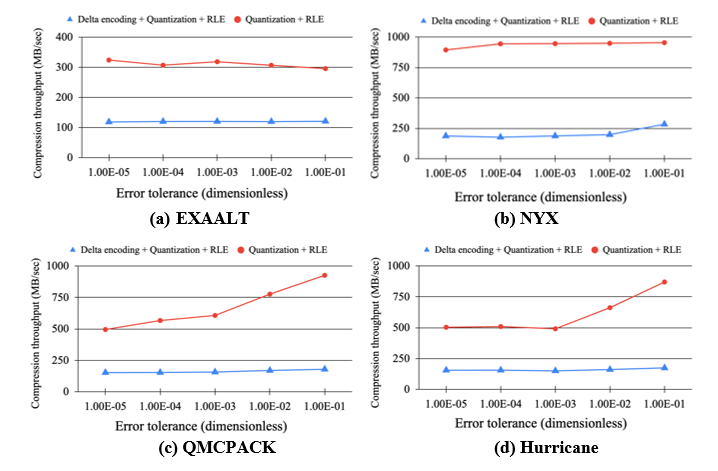
Overall, the delta encoding performs relatively better at tight error bounds. As the error bound loosens, direct quantization can increasingly accommodate data points into a single bucket, and therefore outperforms delta encoding substantially. Contrary to the common belief, delta encoding does not consistently improve the compressibility of data. For example, for NYX data, as shown in Fig. 3(b), which is highly compressible, delta encoding makes the overall performance worse as compared to case 1. This is because RLE requires the strict consecutive occurrence of symbols to compress data, and delta encoding can reduce the length of a run in RLE. On the other hand, it is observed that the compression ratios of the EXAALT data are less than one (Fig. 3(a)), indicating that compression is not beneficial in this case. This behavior is largely attributed to RLE, where the run-length pair can increase the data size if there are no repeated symbols. For NYX, on the other hand, both cases can result in highly repeated symbols leading to an efficient RLE performance and high compression ratios. Fig. 4 evaluates the compression throughput for the four datasets across error bounds. Although case 1 involves less computation, it has a much higher throughput than case 2.

Fig. 5 further illustrates a scientific visualization of NYX. In particular, the left subfigure shows the baryon density of the original data, while the right subfigure shows the visualization of the reduced data with an error tolerance of 1E-5. Overall, it is observed that the reduction maintains a decent fidelity of the data with error control. Tables 1 and 2 further compare delta encoding with two state-of-the-art compressors, SZ and ZFP, concerning compression ratios and throughput, respectively. It is demonstrated that delta encoding offers an alternative to these tools, providing either higher compression ratios or improved throughput in certain scenarios. Tables 3 and 4 further break down the computational cost of compressing and decompressing NYX, respectively. In particular, the pipeline of compression/decompression is broken into delta encoding/decoding, quantization/dequantization, and RLE/RLD. While the delta encoding is the most time-consuming step, RLE consumes the largest memory space, as it needs to reserve extra space in case the data is not highly compressible. Fig. 6 plots the error distribution for all datasets at the relative error of 1E-1. Overall, the results show that the errors are mostly in either Gaussian or Uniform distribution, which largely depends on the characteristics/compressibility of the data.

This work aims to design an error control scheme for delta encoding. The results show that a wide range of errors can be satisfied using the proposed design. This work is limited to using RLE as the back-end lossless compression algorithm. As aforementioned, RLE requires consecutively repeated symbols to reduce data. This stringent requirement often leads to lower compression ratios. Future research will study more advanced algorithms, such as the Huffman tree, which can capture and compress non-consecutive repeated symbols, and examine the performance of delta encoding. On the other hand, a simple uniform quantization scheme is utilized in this paper to convert data to buckets. More adaptive quantization can be used to enhance compression efficiency and accuracy. Overall, it is observed from this work that the error control scheme needs to be carefully designed, and its performance is highly sophisticated depending on many factors, including the complexity of the algorithm and the back-end lossless compressor.

Conclusion and Future Work

This paper proposes a delta encoding scheme with error control for reducing scientific data. We implement it using the C language and evaluate the performance of delta encoding across four real datasets. By using the reconstructed value of the previous data point as a reference, we can effectively bound the error. Regarding performance, the added delta encoding improves the performance as compared to the state-of-the-art in certain scenarios, and thus can be considered to be incorporated into existing tools. For future work, we will test delta encoding and RLE for a wider range of data from different domains with different characteristics. More in-depth studies of other lossless compression algorithms, such as the Huffman tree, and adaptive quantization schemes, will be conducted in future work. In particular, the Huffman tree is a more promising technique than run-length encoding because it does not require repetitive symbols to occur consecutively. As such, the Huffman tree can better compress data. Meanwhile, the idea of adaptive quantization is that for data ranges where more data points fall, smaller buckets can potentially reduce the error.

References

1. WikiChip. Summit (OLCF – 4) – Supercomputers, (2018). [↩]
2. Zstandard. Fast real-time compression algorithm(2025). [↩]
3. J. Gailly, M. Adler, Zlib, www.zlib.net (2024). [↩]
4. S. Di and F. Cappello, Fast Error-Bounded Lossy HPC Data Compression with SZ, 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Chicago, IL, USA, 2016, pp. 730-739, doi: 10.1109/IPDPS.2016.11. (2016) [↩]
5. Peter Lindstrom, Fixed-Rate Compressed Floating-Point Arrays, IEEE Transactions on Visualization and Computer Graphics, 20(12): 2674–2683, (2014) [↩]
6. X. Liang et al., MGARD+: Optimizing Multilevel Methods for Error-Bounded Scientific Data Reduction in IEEE Transactions on Computers, vol. 71, no. 07, pp. 1522-1536, doi: 10.1109/TC.2021.3092201. (2022) [↩]
7. https://github.com/katezhxng/Delta.git [↩]