From static to adaptive: a performance and representational analysis of competitive MARL training paradigms

Abstract

Competitive multi-agent reinforcement learning (MARL) presents unique challenges in balancing dynamic adaptation with strategic diversity, particularly when comparing architectures that employ static versus adaptive opponent training. This study investigates the relationship between training methodology and emergent behavior by analyzing two distinct approaches: 1. Simultaneous Competitive Training (SCT): Both teams of agents learn together, where each agent’s policy updates in response to the evolving strategies of its opponents. 2. Frozen Opponent Training (FOT): Learning agents compete against static versions of themselves frozen after post-foundational training. Through an examination of tactical development, representational learning, and policy dynamics in a zero-sum lunar lander environment—a competitive 2D simulated game domain where two spacecraft teams containing descenders and attackers fight for control of a central landing zone—we uncover fundamental differences in how these algorithms shape agent behavior. Our analysis demonstrates that adaptive training (SCT) fosters richer strategies and more complex state representations, while static opponent algorithms (FOT) lead to constrained policy evolution. SCT agents developed more distinct tactics, including rushing, recoverable ramming, and baiting against FOT agents. Representatively, SCT agents exhibited a higher AUC in state discriminations via t-SNE clustering for 2 out of 3 tactical states. They also demonstrated direct spatial encoding, whereas FOT agents tended to overfit inefficiently. In terms of adaptability, SCT agents showed cubic reward progression with an r² of 0.962, maintained high KL-divergence indicative of ongoing exploration, and achieved a 3.74-meter improvement in landing precision despite environmental drift. In contrast, the performance of FOT agents declined, with accuracy becoming negatively correlated over time (r = -0.83). The analysis extends beyond performance metrics to explore how training frameworks influence the very nature of competitive interaction, offering insights into the mechanisms that drive MARL systems.

Keywords: Physics-based Simulation and Control, Multi-Agent, Data Science, machine learning, Deep Learning; Reinforcement Learning, Neural Network

Introduction

Recent advances in Single-Agent Reinforcement Learning (SARL) have demonstrated potential for developing autonomous systems capable of sophisticated coordination. Lee et al.’s muscle-actuated human simulation¹ showed how deep reinforcement learning can master complex motor skills in high-dimensional musculoskeletal systems. However, while such single-agent systems excel at individual skill acquisition, they cannot address multi-agent coordination, particularly in competitive environments where agents must dynamically adapt to opponents and where imitation data may be unavailable. Multi-Agent Reinforcement Learning² (MARL) presents a solution, offering the potential for autonomous agents to learn competitive and cooperative strategies in complex, physics-based environments. This capability is crucial for real-world applications involving multiple decision-making entities, ranging from autonomous vehicles coordinating traffic flow³ to robotic systems operating in warehouse logistics⁴, where interactions between agents and their environment define the problem space. Despite these advances, MARL often trains against static or pre-trained opponents⁵,⁶,which may limit its adaptability in dynamic scenarios. Such agents fail catastrophically when faced with novel strategies⁷ a gap our work attempts to quantify through tactical and representational analysis. A common approach to manage this complexity is to train agents against static or pre-trained versions of themselves⁸. This approach, which we formalize as Frozen Opponent Training (FOT), can yield stable policies by turning the multi-agent problem into a single-agent one against a fixed distribution of strategies. However, a well-documented limitation of this method is that agents may overfit to the specific strategies of their frozen adversaries, leading to a lack of robustness and a failure to generalize when faced with novel tactics⁹. This phenomenon, sometimes referred to as strategy brittleness, means such agents can “fail catastrophically” against strategies outside their training distribution¹⁰,¹¹. In contrast, an alternative way embraces non-stationarity by having all agents learn simultaneously. This approach, which we term Simultaneous Competitive Training (SCT), is grounded in the concept of self-play, famously used to train human-like agents in soccer¹² and implemented in mini-games such as OpenAI’s hide-and-seek agents¹³. The core hypothesis is that continuous mutual adaptation drives an arms race of increasingly sophisticated and robust strategies¹⁴,¹⁵. However, pure self-play can sometimes lead to obsessive cycles or an over-concentration on a narrow set of strategies¹⁶. Recent research has explored methods to encourage diversity and robustness within simultaneous training, such as population-based training¹⁷ and league training¹⁸, which maintains a diverse pool of opponents to prevent overfitting and promote generalizable policies¹⁹,²⁰. This paper directly compares Simultaneous Competitive Training (SCT), in which agents learn concurrently through competition, with Frozen-opponent Training (FOT), in which agents learn against a fixed policy. This test examines whether mutual adaptation yields more robust strategies than those against static opponents. We hypothesize that in our physics-based environment, MARL agents trained with SCT will outperform FOT-trained agents in robustness and strength. Our study makes three key contributions to the field: First, we introduce a novel physics-based multi-agent lunar lander benchmark for MARL research. Second, we present a hybrid training methodology that combines foundational skill acquisition with competitive learning. Third, through systematic head-to-head evaluation, we demonstrate that agents trained in a competitive co-adaptation regime develop measurably stronger strategies than those trained against static opponents.

Methods

The Multi-Agent Learning Challenge

This work examines a MARL problem in which agents are equipped with the ability to use discrete actions to interact with the environment and other agents, to complete an objective. MARL introduces substantially greater complexity than single-agent reinforcement learning due to environmental stochasticity and the inherent interdependence of agents’ learning dynamics². A central challenge in MARL arises from the non-stationarity of the learning process. When one agent updates its policy, the optimal strategies of other agents may become invalid. MARL frameworks are typically classified into two types: competitive and cooperative. In competitive MARL, agents optimize their rewards while actively minimizing those of their opponents, either through explicitly adversarial (zero-sum) incentives or indirectly conflicting objectives. In cooperative MARL, agents align their rewards toward a common goal, with individual contributions collectively advancing system-wide performance. Furthermore, agents may adopt either on-policy or off-policy learning strategies. On-policy methods exclusively learn from actions sampled under the current policy, ensuring consistency but limiting data reuse. Off-policy approaches, while more sample-efficient by leveraging historical experience, risk instability due to discrepancies between past and current policies

Multi-Agent Markov Games

Unlike [Littman, 1994]²¹, who modeled agents in a partially observable setting where each agent only has access to its own local state information, we model our multi-agent system as a fully observable Markov game with K interacting agents. The environment is formally defined by the tuple ⟨ S , A_1, ···, A_K, R_1, ···, R_K, ρ, T ⟩, where S represents the complete set of global states visible to all agents simultaneously, A_i denotes the action space available to agent i, and R_i specifies that agent’s reward function. The game begins with an initial state S_0 drawn from ρ, while the state transition dynamics are governed by the stochastic transition function T : S × A_1 × ⋯ × A_K → ΔS, where ΔS represents the set of probability distributions over S. The game progresses through discrete timesteps in the following sequence. First, all agents observe the current global state s ∈ S. Each agent then independently selects and executes an action a_i from its available action space A_i. These joint actions trigger a state transition to s’, sampled from the distribution T, after which each agent i receives its corresponding reward r_i as determined by its reward function R_i : S × A_1 × ⋯ × A_K → ℝ. This cycle repeats until the game reaches a horizon T. Within this framework, each agent i aims to learn an optimal policy π_i that maps states to actions to maximize its expected cumulative discounted return E[ ∑_{t=0}^{T} γ^{t} r_{i,t} ], where γ ∈ (0,1] represents the standard discount factor applied to future rewards.

The complete observability of state information distinguishes this formulation from partially observable variants, as agents make decisions with full knowledge of the environment state. This general framework can accommodate both competitive and cooperative scenarios through the appropriate design of the reward functions , while the shared global state space provides a simpler learning environment compared to partially observable settings. The stochastic transition function inherently captures both the environmental dynamics and the complex interactions between learning agents.

Figure 1. Multi-agent reinforcement learning (MARL) environment. Illustrates our environment setup, which consists of two agent roles and a shared target zone. A) Descenders (light red/blue): Agents with 4 discrete actions, tasked with maintaining proximity to the landing pad and securing territory. B) Attackers (dark red/blue): Adversarial agents with 5 discrete actions, including projectile attacks to disrupt opponents. C) Landing pad (yellow flags): Target zone for Descenders, positioned at the origin (0,0), serves as the contested objective for both teams. Workflow: Agents are spawned at opposing corners; Descenders navigate toward and try to maintain position near the landing pad, while Attackers actively interfere with the opponents. Team rewards are computed purely based on each team’s descender’s success and act as a feedback loop that guides learning.

Environment

Our competitive multi-agent environment is built upon the Gymnasium Box2D Lunar Lander framework²² modified to support team-based interactions. The simulation space measures 40 meters in width and approximately 26.67 meters in height (800/30 ratio), featuring procedurally generated terrain with varying elevation across different chunks (Figure. 1). Each episode is temporally bounded to 5 seconds of simulated time, with physics updates occurring at 100 frames per second to ensure smooth dynamics. After each episode is finished, a different seed is chosen for the preceding run. The environment hosts two competing teams (red and blue), each composed of two distinct lunar lander variants differentiated by both function and visual design (light and dark coloration). All landers are physically modeled as trapezoidal rigid bodies equipped with two spring-damped landing legs, providing more complex contact dynamics. Both blue landers and red landers start the match at the top right corner and top left corner, respectively. The competitive framework follows an area control paradigm, where teams vie for dominance over a central landing pad positioned at the origin 0,0 . Agent specialization is implemented through differentiated roles and capabilities. The descender agent (dark) is tasked with maintaining stable positioning near the landing pad, while the aggressor agent (light) focuses on disrupting opposing team operations. Action spaces are discretized according to Pontryagin’s maximum principle²³, which dictates optimal binary throttle control. The descender’s action space comprises four discrete commands: null operation (0), left orientation thruster activation (1), main engine activation (2), and right orientation thruster activation (3). The aggressor expands this capability with a fifth action (4), enabling the launch of triangular projectiles.

The observation space is structured as a 32-dimensional vector, constructed by concatenating of each agent’s state representation. For each lander, the state vector s ∈ ℝ⁸ consists of:

s = [x, y, ẋ, ẏ, θ, ω̇, c_l, c_r],

where [x, y] denotes positional coordinates, [ẋ, ẏ] represents linear velocities, θ indicates angular orientation, ω̇ is angular velocity, and c_l, c_r are Boolean contact indicators for left and right landing legs, respectively. This per-agent state vector is stacked across all four agents (two per team) to form the global observation space used for policy inputs. Normalization is applied to each component of the state to maintain numerical stability and ensure consistent input scaling. Specifically: x is centered relative to the horizontal midpoint of the viewport and scaled by half the viewport width:

x_norm = (x − VIEWPORT_w / (2 · SCALE)) / (VIEWPORT_w / (2 · SCALE)),

y is centered relative to the helipad height and scaled by half the viewport height: y_norm = (y − (helipad_y + LEG_down / SCALE)) / (VIEWPORT_H / (2 · SCALE)). Linear velocities are scaled by their respective viewport dimensions and normalized by the simulation framerate (FPS):

ẋ_norm = (ẋ · VIEWPORT_w / (2 · SCALE)) / FPS,   ẏ_norm = (ẏ · VIEWPORT_H / (2 · SCALE)) / FPS. Note that SCALE is 30 meters per pixel. Positional coordinates are constrained to x ∈ [−1.5, 1.5] and y ∈ [−0.5, 1.7], while both linear and angular velocities are clamped to the range [−5, 5]. This normalization scheme prevents gradient explosion during backpropagation while maintaining physically meaningful ranges for all state variables. The reward function is carefully designed to promote stable learning dynamics while discouraging chaotic behavior. For descender agents, the reward r at each timestep is computed as:

r = −10√(x² + y²) − 15√(ẋ² + ẏ²) + 0.5 · Ind[c_l] + 0.5 · Ind[c_r],

where Ind denotes the indicator function for leg-ground contact events. This formulation combines three key components: (1) a quadratic penalty on displacement from the origin that grows with distance, (2) a velocity-dependent penalty to encourage smooth maneuvers, and (3) positive reinforcement for successful leg contacts. All agents receive an additional boundary violation penalty: r = r − 20 · Ind[|x| > x_max ∨ |y| > y_max] where x_max and y_max represent the horizontal and vertical boundaries, respectively. This harsh penalty strongly discourages agents from exiting the valid simulation space while maintaining differentiable gradients within the permitted operating region. The reward system implements a competitive zero-sum framework through team-based reward aggregation. For each team T ∈ {Red , Blue}, the collective team reward R_T is computed as the summation of individual agent rewards within that team: R_T = ∑_i∈T r_i, where r_i represents the reward for agent i as defined in the previous section. The net reward R̃_T for each team is then calculated as: R̃_T = R_T − R_−T where −T denotes the opposing team. This differential reward structure ensures strict zero-sum competition, as R̃_Red + R̃_Blue = 0 by construction. The zero-sum formulation naturally emerges from the competitive nature of the environment, where one team’s gain corresponds directly to the opponent’s loss.

Algorithm Selection

Several algorithms exist for solving MARL problems. One prominent MARL algorithm is Multi-Agent PPO (MAPPO)²⁴, which employs Centralized Training with Decentralized Execution (CTDE). In MAPPO, agents utilize a centralized critic during training that has access to global state information, enabling better cooperation and more accurate value estimation. During execution, however, agents operate independently using only their observations. While MAPPO and other MARL algorithms such as QIMIX, MADDPG, and related methods were considered, practical constraints limited their applicability. Many of these algorithms are deprecated in popular libraries and have limited integration with the Gymnasium API. Therefore, we opted for Proximal Policy Optimization (PPO)²⁵, which provides a well-supported and stable baseline, allowing for reproducible experimentation in our competitive multi-agent setting. PPO is an on-policy reinforcement learning algorithm that optimizes a clipped objective function to ensure stable policy updates. PPO maintains two policy networks – an active policy that interacts with the environment and another policy used for importance sampling, which are periodically synchronized. The key advantage of PPO lies in its surrogate objective function:

L^CLIP(θ) = E_t [ min ( r_t(θ) A_t, clip ( r_t(θ), 1 − ε, 1 + ε ) A_t ) ]

where r_t(θ) represents the probability ratio between new and old policies, A_t denotes the advantage estimate, and ε is a hyperparameter that constrains policy updates.

This clipped objective prevents excessively large updates that could destabilize training, while the advantage normalization promotes more consistent gradient estimates. We implemented PPO with separate policy networks for each agent to accommodate their specialized roles. Two distinct architectural approaches were evaluated. Shared Policy Architecture: This approach utilized a single model governing all agents within a team, outputting a multi-discrete action space that represented the combined actions. The model received a one-hot encoded vector to distinguish between agents. However, this implementation demonstrated poor convergence properties, particularly given the distinct roles and action spaces of our agents. The shared representation proved insufficient for capturing the specialized behaviors required by each agent’s unique responsibilities.

Independent Policy Architecture: Our final implementation assigned each agent its policy model (Figure. 2). This approach proved significantly more effective, as it allowed each agent to develop specialized behaviors tailored to its specific role and action space. The independent policies converged more reliably and achieved substantially better performance compared to the shared policy approach.

Hyperparameter	Value	Description
Number of steps	2048	Steps to collect before each update
Batch size	64	Size of minibatches used for training
Number of epochs	10	Number of training passes over each batch
gamma	0.99	Discount factor for future rewards
Gae lambda	0.95	Controls bias-variance tradeoff in GAE
Clip range	0.2	PPO clipping parameter
Learning rate	3e-4	Optimizer learning rate
Entropy coefficient	0.0	Entropy bonus to encourage exploration
Value function coefficient	0.5	Weight for value function loss
Max gradient normalization	0.5	Gradient clipping threshold
Network architecture	[64, 64]	Hidden layer sizes for both policy and value networks
Activation function	tanh	Activation function used in network layers

Table 1. Hyperparameters of each agent’s model. Specifications used in the PPO algorithm with an MLP policy, as implemented in the Stable-Baselines3 library. These values represent the default, standard settings commonly used in reinforcement learning and are provided for reproducibility. No additional hyperparameter tuning was performed, as these standard values generally support stable training of PPO agents in any environment.

Algorithm Implementation

All agents, whether destined for Simultaneous Competitive Training (SCT) or Frozen Opponent Training (FOT), first completed identical foundational training. Learning effective control policies in this high-dimensional, stochastic environment presents significant challenges. The inherent non-stationarity of observations (OBS) and the moving target problem frequently leads to poor policy convergence and task failure. While imitation learning approaches using motion capture data have proven successful in other domains, the unique structure of our environment precludes this option due to the lack of suitable demonstration data. Manual piloting to generate training data was also considered but ultimately rejected, both due to the extreme difficulty of manual control and our desire for agents to discover novel control strategies autonomously. To address these challenges, we developed a phased foundational training approach that closely parallels curriculum learning²⁶ where agents are gradually exposed to increasing levels of task complexity to stabilize learning and improve sample efficiency. In the initial isolation phase, we train individual policies while freezing all other agents’ actions (setting them to null operations). For instance, when training policy , we disable action prediction for , , and . During this phase, the reward function considers only the rewards of the training agent. After establishing basic competencies, we gradually introduce opposing team agents into the environment, allowing them to predict (but not update) actions while incorporating their respective rewards into the training regime. Note that the training agent’s teammate was not allowed to predict during this process, particularly because we found that agents started sacrificing their primary objectives to compensate for teammate errors. The second phase trained teammate’s policies while maintaining frozen opponent policies. This stage cultivates essential team coordination skills such as collision avoidance and goal alignment. The same process is then replicated for the opposing team. Each policy underwent approximately 24 hours of this foundational training. The competitive training diverged based on this methodology: For the SCT Group, both teams trained simultaneously with full policy updates enabled across all agents (Team A vs Team B). For the FOT Group, Team C underwent training while competing against a static, inference-only Team D that maintained its foundational training parameters without further updates. Our evaluation compares the final SCT Team A versus the final FOT Team C. The complete reward function was implemented with round-robin training, where each policy received 250,000 updates before rotating to the next learning agent. Both SCT and FOT configurations underwent identical training durations of 21 million timesteps. A Comparative evaluation was conducted at five checkpoints (0, 4, 9, 15, and 21 million timesteps), where teams were assessed over 1 million inference timesteps. To accelerate training, we employ a subprocessed), which parallelizes environment instances across multiple CPU cores (we used 4). This architecture enables the simultaneous execution of episodes with synchronous state aggregation, where experience tuples from all parallel instances are collected and batched before each policy update. All training metrics and results were logged and analyzed using TensorBoard for comprehensive performance monitoring. This phased strategy functions analogously to curriculum learning by structuring exposure to difficulty, rather than forcing agents to learn all aspects of the task simultaneously. Random initialization without such phasing would likely slow convergence and increase policy instability²⁷, as agents would face the full complexity of the competitive environment from the outset. A Systematic exploration of these initialization strategies remains an important direction for future research. Additionally, while SCT, like other MARL approaches, could in principle diverge, in our experiment, however, we did not observe divergence or catastrophic instability across multiple seeds. We attribute this, in part, to our normalization scheme²⁸ and clipped PPO objectives. Nevertheless, systematically analyzing SCT’s stability under more challenging conditions is another interesting direction for future research.

Results

This study compares SCT and FOT to evaluate whether dynamic co-adaptation yields superior tactical diversity, representational learning, and competitive performance overstatic opponent paradigms in multi-agent reinforcement learning. All agents completed identical foundational training (24 hours/policy) before diverging into SCT or FOT, with SCT enabling co-adaptive learning between teams and FOT using static opponents, followed by evaluation at five checkpoints over 21 million timesteps. SCT agents achieved consistently higher net rewards than FOT agents across all post-baseline evaluations with a mean reward of 493.7 (Figure. 3 A1). Compared to the pre-trained baseline of –44.9, this represents a dramatic improvement of over 1,100%, with reward progression following a strong cubic trend (r² = 0.953, Figure. 3 A2).

	Inference Session 1	Inference Session 2	Inference Session 3	Inference Session 4	Inference Session 5
Standard Deviation (STD)	22.913	47.068	61.786	79.301	90.328
Range	[−95.079, −6.656]	[14.556, 208.254]	[289.940, 532.973]	[96.152, 501.615]	[297.010, 639.294]
95% Confidence Interval (CI)	[−51.161, −38.653]	[84.466, 110.160]	[369.016, 402.745]	[359.597, 402.887]	[469.088, 518.398]

Table 2. Reward Variability Metrics for each Inference Session. Data were collected during inference sessions (deterministic policies) at 0, 4, 9, 15, and 21 million training timesteps. For each checkpoint, the FQT (red) and SCT (blue) teams were evaluated over 1 million timesteps (2,000 episodes), with the data calculated after clipping outliers (5th–95th percentile). This table reports the standard deviation, range, and 95% confidence interval of the average reward obtained during each inference session in Figure 3a. The statistics quantify the variability and reliability of each team’s performance during inference.

While mean rewards increased over training, the standard deviation, range, and 95% confidence intervals reveal notable variability between sessions. For example, early sessions (0M timesteps) exhibited relatively low variability (STD = 22.9, 95% CI [-51.2, -38.7]), whereas later sessions (21M timesteps) showed higher variability (STD = 90.3, 95% CI [469.1, 518.4]) (Table 2).

Behavioral Analysis

Qualitative analysis quantified strategy development across 7 tactical categories (Figure 4). Attackers in both groups progressed from basic stable flying and aiming to more advanced tactics, including Camping, Close-Quarters approaches, and Ramming. v1 (Figure. 4 A, C, D). However, the development of more sophisticated behaviors like Ramming. v2 – where Attackers learned to recover from missed attempts – was significantly less consistent in the FOT-trained Attacker (Figure. 4 G). The FOT-trained Descender failed to develop key strategies that were present in the SCT Descender, particularly Rushing and Dodging maneuvers (Figure. 4 B, F).

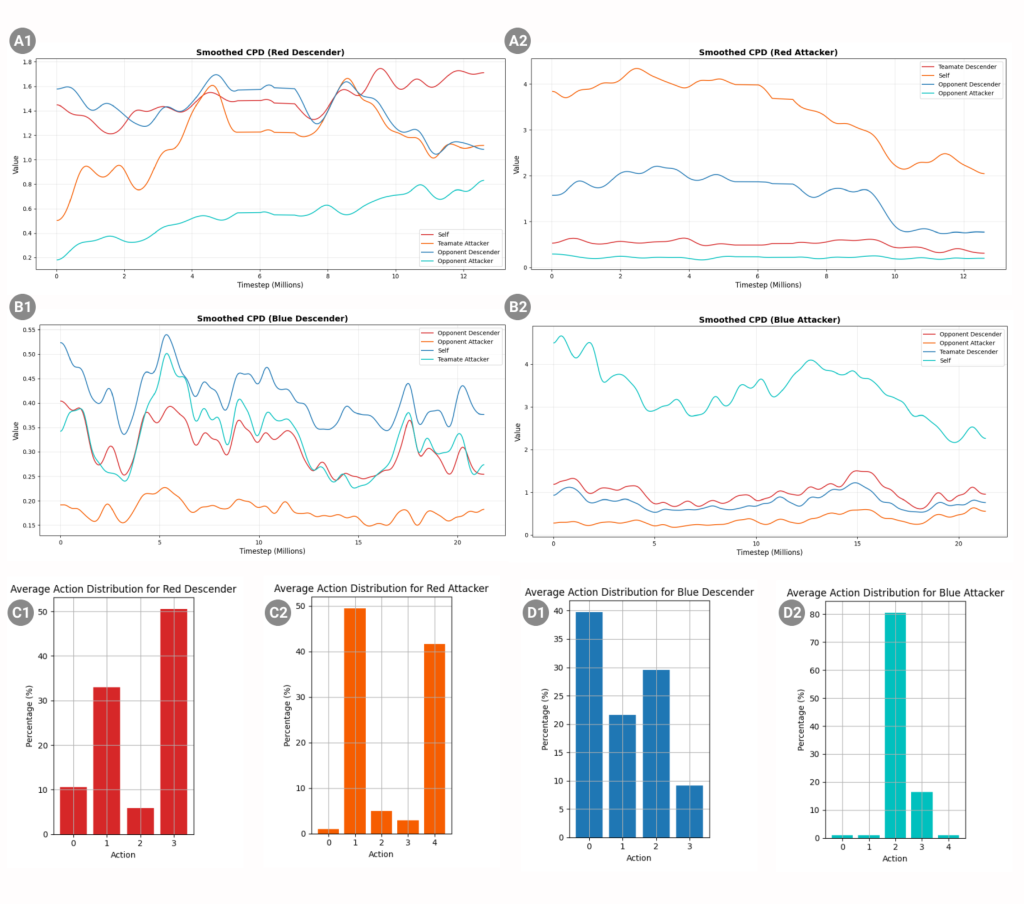
Counterfactual policy divergence (CPD) and action distribution across training for FQT (red) vs SCT (blue).
(A1–B2) shows the smoothed CPD of how each agent’s behavior depends on the other agents’ positions, calculated as:
,
where is the policy of agent (a) given the full state (s), (D) is the distribution of original states (s) encountered during gameplay, (R_b(s)) is a resampling distribution where only agent (b)’s position is replaced randomly, while all other components of (s) stay fixed, (s’) is the modified state where (b)’s position is perturbed, and is the KL divergence between the policy distributions before and after perturbation. Higher values indicate stronger influence.
(C1–D2) shows the action distribution histograms from the final inference (21M steps). Action distributions were logged over 1M deterministic inference steps.

The action distribution patterns revealed that the FOT descender exhibited a 2.72x stronger bias toward lateral thrust actions (left=1, right=3), compared to the SCT descender (Figure. 5 C1, D1). This contrast was particularly evident in Attacker behavior: the FOT Attacker overwhelmingly favored left thrust (analogous to the SCT’s attacker’s right thrust) which was used three times more frequently and the firing action was used 42 times more frequently, whereas the blue attacker primarily employed main thrust (16x higher) with moderate right thrust usage (Figure. 5 C2, D2).

Our comparative analysis of performance metrics revealed systematic differences between FOT and SCT-trained agents across all measured dimensions (Average Cohen’s d=0.6552) (Figure. 6 B1-B5). Accuracy trajectories showed an obvious divergence: while the SCT Attacker maintained stable accuracy (μ=0.55±0.21) with slight improvement over time (r=0.38), the FOT Attacker exhibited a significant downward trend (r=-0.83), declining from initial superiority to substantially lower final accuracy (Δ=97%, p<0.08, Cohen’s d=0.61) (Figure. 6 B1). The aggression metric demonstrated particularly striking differences (Cohen’s d = 0.633) (Figure. 6 B2). Although both groups showed comparable aggression levels during early training (0-15M timesteps), the SCT attacker displayed a dramatic late-stage surge to 2,544,180 aggression units – 21,202× higher than FOT’s peak (12 units). Recovery dynamics revealed an important learning pattern (Cohen’s d=1.013) (Figure. 6 B3). While the FOT Descender initially showed superior recovery (11 vs. 23 steps), this relationship inverted by 4 million timesteps, with the SCT Descender achieving consistently better recovery (final Δ = -6 steps). Positional analysis showed the SCT Descender establishing significantly better landing pad proximity than the FOT Descender (Position=3.74m) after 9M timesteps (Cohen’s d=0.217) (Figure. 6 B4). Notably, both groups showed a deteriorating relative position over time, although the SCT Descender maintained a persistent advantage (Cohen’s d = 0.803). Stability metrics confirmed the SCT Descender’s superior control, with 6110% less speed variance (F = 62.32, p < 0.001) until the final timestep when both groups showed expected strategy-induced instability (Figure. 6 B5).

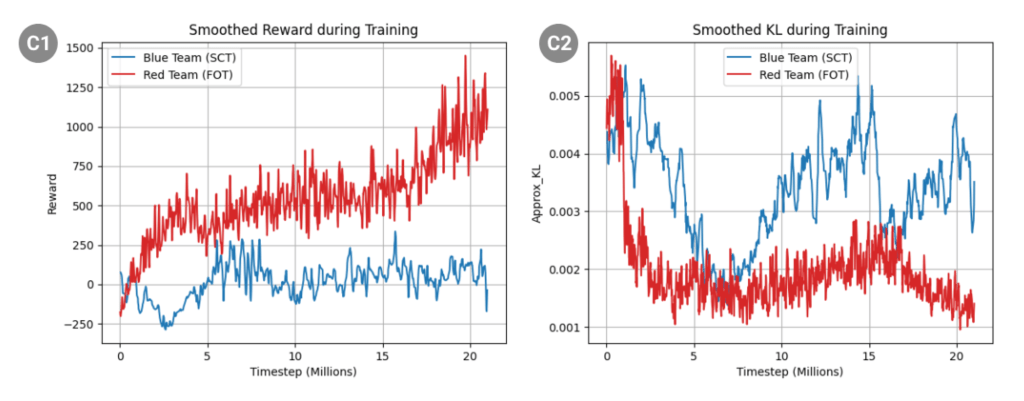
Training showed SCT’s oscillating rewards (σ²=1.92× higher) and maintained high KL divergence reflect active strategy evolution, while FOT’s reward and KL convergence monotonically increased (Figure. 7 C1-C2).

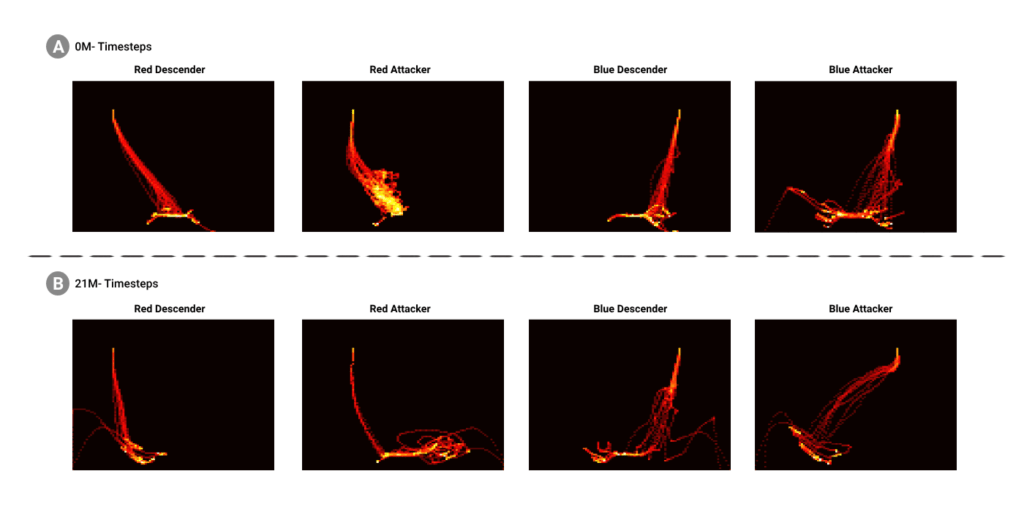
Heatmap analysis showed the SCT Descender with greater movement diversity and the Attacker taking more direct interception paths (Figure. 8).

Representational Analysis

The t-SNE visualization of latent features showed clear differences in how FOT and SCT agents represent important game states (Figure 9). For descender proximity to the landing pad, the FOT Descender had scattered and poorly separated representations, while the SCT Descender’s features formed a distinct cluster in the northeast quadrant (Figure 9 A1, B1). This pattern appeared again for descender-attacker proximity, with the SCT Descender showing organized clustering in the same area (Figure 9 A2, B2). When looking at the proximity of attackers to the opponent’s descender, both teams had similar distributions, clustering in southern regions, though blue was grouped a bit more tightly (Figure 9 A3, B3). Representational efficiency metrics highlighted several key differences (Figure 9 E1-F3). For landing pad proximity, the FOT Descender followed the pattern MLP > raw > LR, which means their internal representations encoded proximity information in a nonlinear but useful way (Figure 9 E1). In contrast, the SCT Descender showed raw > MLP > LR, suggesting this spatial information was more directly available in the observations than in their internal representations (Figure 9 F1). In the Descender-Attacker proximity task, the FOT Descender performed well across all inputs, indicating that proximity information was available in both raw and learned features (Figure 9 E2). The SCT Descender showed a similar trend, (raw = MLP) > LR, which suggests their representations captured the relevant features, but these were not linearly separable (Figure 9 F2). For the Attacker-Descender proximity task, FOT’s Attacker showed MLP > (raw = LR), again relying on nonlinear structure in their internal representations (Figure 9 E3). The SCT Attacker showed MLP > raw > LR, which demonstrates both rich internal encoding and moderate linear separability of features (Figure 9 F3). Neuron activation analysis (AUC metrics) revealed notable differences in state processing (Figure 9 C1-D3). For landing pad proximity, both teams had similar discriminative ability (FOT AUC: 0.738, SCT AUC: 0.731), with stronger activation for “far” states in both cases (Figure 9 C1, D1). In the descender-attacker proximity analysis, the SCT Descender achieved 1.17% better separation (0.777 vs FOT’s 0.768), with the FOT Descender showing a strong focus on far states. At the same time, SCT maintained more balanced activation (Figure 9 C2, D2). The biggest difference was in attacker-descender proximity processing: the FOT Attacker focused mainly on avoidance (0.686, far-state focus), while the SCT Attacker showed 6.12% better discrimination (0.728) with a clear emphasis on near states (Figure 9 C3, D3). Counterfactual policy divergence measurements gave more insight into decision-making (Figure 5 A1-B2). Both FOT and SCT Descenders emphasized opponent and teammate states in their policies, showing similar social awareness (Figure 5 A1, B1). However, attackers differed: the FOT Attacker prioritized opponent states, while the SCT Attacker showed more self-interested policies (Figure 5 A1-B2).

Discussion

Our comparative analysis of SCT and FOT shows clear differences in how agents perform, behave, and learn. In our tests, SCT-trained agents perform better tactically and were more robust and adaptable then FOT agents. For example, SCT agents earned much higher net rewards (mean: 364.9) compared to FOT agents, which is an 11,000% improvement over the baseline. Although reward variability increased across inference sessions, we did not interpret this as an indication of training instability. Rather, the increasing variability reflects that the agents were adopting riskier, higher-reward strategies to maximize performance (an indication of exploration and adaptability). Early sessions are more uniform because policies were conservative, leading to lower rewards. The SCT Attacker developed advanced strategies (e.g., Ramming.v2) that the FOT Attacker did not. The rapid progression in rewards (r² = 0.962) suggests that SCT helps agents learn skill quickly under adversarial pressure. In contrast, FOT agents showed little improvement, with declining accuracy (r = -0.83) and minimal aggression (up to 21,202 times lower than SCT)—reflecting an inability to adapt beyond the fixed opponent’s skill level. FOT agents also showed a strong bias for lateral thrust (2.72 times more), suggesting poor development from older strategies. In contrast, SCT agents dynamically balance thrust and other actions, enabling them the ability to execute a variety of tactics. The SCT Attacker used main thrust maneuvers 16 times more often, matching the ramming strategies analyzed in our behavioral analysis. FOT attacker relied much more on firing (42 times higher), missing out on the better strategies discovered by SCT. Recovery and positional metrics further indicate that SCT-trained agents exhibit stronger performance in this environment. While the FOT Descender initially led in recovery steps, the SCT Descender inverted this trend by mid-training, ultimately achieving 6 fewer steps per recovery. Similarly, the SCT Descender maintained a closer proximity of 3.74 m to the landing pad, demonstrating better positional optimization despite both groups exhibiting drift over time. SCT Descenders had much lower speed variance (6110% less), showing more stability, except during late-stage strategy changes like deliberate ramming. Visualizations and neuron analyses show SCT and FOT agents process game states differently. SCT Descenders formed clear clusters for important states, like being new the landing pad, while FOT agents’ representations, were scattered, making it harder to tell states apart. SCT agents also encoded proximity between Attacker and Descender more precisely (6.12% higher AUC), focusing on getting close for interception, while FOT Attackers focused on staying away. In terms of learning, FOT agents needed complex decoding, while SCT agents used raw observations more effectively, suggesting they learned spatial relationships better. The counterfactual policy analysis revealed an unexpected finding: while both teams’ descenders weighted teammate/opponent states similarly, the SCT attacker prioritized self-reward over cooperation, unlike the FOT attacker, which focused on opponents—potentially an artifact of static adversaries. Overall, SCT’s co-evolutionary setup encourages a wider range of strategies, while FOT tends to get stuck on local optima, which matches known issues with fixed-opponent setups5. This difference also shows up in how agents learn: SCT agents formed more organized internal representations, while FOT agents’ encodings were more redundant and less efficient. Training patterns highlight these differences: SCT agents’ rewards fluctuated and showed high KL-divergence, indicating active exploration, while FOT agents’ rewards stabilized too early. Still, there are three important caveats to SCT’s advantages: (1) we have not tested its effectiveness in purely cooperative tasks, (2) dynamic training may require more computing resources than FOT, and (3) the SCT attacker’s focus on self-reward needs more study to see if it comes from reward design or competition. In our Lunar Lander tests, SCT-trained agents outperformed FOT agents in tactics, learning speed, and adaptability. While these results are promising for dynamic adversarial training, future research should test if these findings hold in other environments, with different tasks, algorithms, and reward systems.

1. S. Lee, M. Park, K. Lee, J. Lee. Scalable muscle-actuated human simulation and control. ACM Trans Graph. 38(4), 1–13 (2019). [↩]
2. K. Zhang, Z. Yang, T. Başar. Multi-agent reinforcement learning: a selective overview of theories and algorithms. In Handbook on Reinforcement Learning and Control (Springer Studies in Systems, Decision and Control) (2021). arXiv:1911.10635 [cs.LG]. [↩] [↩]
3. L. Lin, X. Nie, J. Hou. Robust multi-agent reinforcement learning for autonomous vehicle in noisy highway environments. Proc Mach Learn Res. 260, 1320–1335 (2025). [↩]
4. J. Huang. Diffusion models for offline multi-agent reinforcement learning with safety constraints. arXiv:2407.00741 cs.AI. [↩]
5. M. Lanctot, V. Zambaldi, A. Gruslys, A. Lazaridou, K. Tuyls, J. Perolat, D. Silver, T. Graepel. A unified game-theoretic approach to multiagent reinforcement learning. Adv Neural Inf Process Syst. 30 (2017). arXiv:1711.00832 [cs.AI]. [↩]
6. T. Bansal, J. Pachocki, S. Sidor, I. Sutskever, I. Mordatch. Emergent complexity via multi-agent competition. Int Conf Learn Represent (2018). arXiv:1710.03748 [cs.AI]. [↩]
7. L. Pinto, J. Davidson, R. Sukthankar, A. Gupta. Robust adversarial reinforcement learning. Proc Mach Learn Res. 70, 2817–2826 (2017). [↩]
8. R. Zhang, Z. Xu, C. Ma, C. Yu, W.-W. Tu, W. Tang, S. Huang, D. Ye, W. Ding, Y. Yang, Y. Wang. A survey on self-play methods in reinforcement learning. arXiv:2408.01072 cs.LG. [↩]
9. A. Kulkarni, S. Zhang, M. Behl. CRASH: Challenging reinforcement-learning based adversarial scenarios for safety hardening. arXiv:2411.16996 cs.AI. [↩]
10. J. Uesato, A. Kumar, C. Szepesvári, T. Erez, A. Ruderman, K. Anderson, M. Krishmamurthy, D. Dvijotham, N. Heess, P. Kohli. Rigorous agent evaluation: An adversarial approach to uncover catastrophic failures. arXiv:1812.01647 cs.LG. [↩]
11. Z. Kenton, A. Filos, O. Evans, Y. Gal. Generalizing from a few environments in safety-critical reinforcement learning. arXiv:1907.01475 cs.LG. [↩]
12. S. Liu, G. Lever, Z. Wang, J. Merel, S. M. A. Eslami, D. Hennes, W. M. Czarnecki, Y. Tassa, S. Omidshafiei, A. Abdolmaleki, N. Y. Siegel, L. Hasenclever, L. Marris, S. Tunyasuvunakool, H. F. Song, M. Wulfmeier, P. Muller, T. Haarnoja, B. D. Tracey, K. Tuyls, T. Graepel, N. Heess. From motor control to team play in simulated humanoid football. arXiv:2105.12196 cs.LG. [↩]
13. C. Baker, I. Kanitscheider, T. Markov, Y. Wu, G. Powell, B. McGrew, I. Mordatch. Emergent tool use from multi-agent interaction. arXiv:1909.07528 cs.AI. [↩]
14. R. Miikkulainen, K. O. Stanley. Competitive coevolution through evolutionary complexification. arXiv:1107.0037 cs.AI. [↩]
15. D. Cliff, G. F. Miller. Tracking the red queen: Measurement of adaptive progress in coevolutionary simulations. In Advances in Artificial Life: Proceedings of the Third European Conference on Artificial Life (Springer-Verlag, Berlin), pp. 200–208 (1995). [↩]
16. D. Hernandez, K. Denamganai, S. Devlin, S. Samothrakis, J. A. Walker. A comparison of self-play algorithms under a generalized framework. arXiv:2006.04471 cs.AI. [↩]
17. M. Zhou, Z. Wan, H. Wang, M. Wen, R. Wu, Y. Wen, Y. Yang, W. Zhang, J. Wang. MALib: A parallel framework for population-based multi-agent reinforcement learning. J Mach Learn Res. 24(150), 1–12 (2023). [↩]
18. K. R. McKee, J. Z. Leibo, C. Beattie, R. Everett. Quantifying the effects of environment and population diversity in multi-agent reinforcement learning. arXiv:2102.08370 cs.LG. [↩]
19. O. Vinyals, I. Babuschkin, W. M. Czarnecki, M. Mathieu, A. Dudzik, J. Chung, D. Choi, R. Powell, T. Ewalds, P. Georgiev, J. Oh, D. Horgan, M. Kroiss, I. Dunning, S. Kim, P. Blunsom, D. Silver, K. Kavukcuoglu. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature. 575, 350–354 (2019). [↩]
20. Q. Fu, X. Ai, J. Yi, T. Qiu, S. Wang, Y. Liu, H. Xu, J. Zhang, J. Pan. Learning heterogeneous agent cooperation via multiagent league training. arXiv:2211.11616 cs.LG. [↩]
21. M. L. Littman, Markov games as a framework for multi-agent reinforcement learning, Mach Learn Proc. 1994, 157–163 (1994). [↩]
22. Gymnasium Contributors. Lunar lander (v2) – a classic rocket trajectory optimization problem. Farama Foundation (2023). URL: https://gymnasium.farama.org/environments/box2d/lunar_lander/ [↩]
23. L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze, E. F. Mishchenko. The Mathematical Theory of Optimal Processes. Wiley (1962). [↩]
24. C. Yu, A. Velu, E. Vinitsky, J. Gao, Y. Wang, A. Bayen, Y. Wu. The surprising effectiveness of PPO in cooperative, multi-agent games. Adv Neural Inf Process Syst. 35 (2022). arXiv:2103.01955 [cs.LG]. [↩]
25. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, O. Klimov. Proximal policy optimization algorithms. arXiv:1707.06347 cs.LG. [↩]
26. R. Bhati, S. K. Gottipati, C. Mars, M. E. Taylor. Curriculum learning for cooperation in multi-agent reinforcement learning. arXiv:2312.11768cs.AI. [↩]
27. J. Chen, Y. Zhang, Y. Xu, H. Ma, H. Yang, J. Song, Y. Wang, Y. Wu. Variational automatic curriculum learning for sparse-reward cooperative multi-agent problems. arXiv:2111.04613 cs.AI. [↩]
28. K. Mehta, A. Mahajan, P. Kumar. Effects of spectral normalization in multi-agent reinforcement learning. arXiv:2212.05331 cs.LG. [↩]