Isoperimetric Inequality

January 29, 2026

Abstract

In this paper, we will prove the Isoperimetric inequality, which states that for any simple closed curve with perimeter $L$ and area $A$ , the inequality $L^2 \ge 4\pi A$ must hold, with equality only when the curve is a circle. Our proof follows Adolf Hurwitz’s analytic route. We will use Fourier series and Parseval’s theorem to obtain Wirtinger’s inequality, which will be applied to a curve written in arc-length form. This path is interesting because it reaches a classic geometry result using mostly algebra and basic calculus instead of geometry. This paper gives a clear, complete walk-through of Hurwitz’s proof, written so students can follow every step without gaps.

Introduction

The Isoperimetric problem studies which shape encloses the greatest area for a fixed perimeter. An early illustration of the problem is the story of Queen Dido and the founding of Carthage. According to the legend, Dido was allowed as much land as she could surround with one oxhide, which she cut into thin strips and arranged along the coast to enclose as large a region as possible. This story captures the central idea that the circle is the most efficient shape for enclosing area with a given boundary length.¹

The formal result is the Isoperimetric inequality, which states that for any simple closed curve with perimeter $L$ and enclosed area $A$ , the relationship

$L^2 \ge 4\pi A$

holds, with equality only for a circle. Although the statement is simple and straightforward, the proof is not immediate. In this paper I will explain Adolf Hurwitz’s analytic proof²^‘³, chosen for its algebraic precision and clear structure. The argument uses Fourier series and Parseval’s theorem to derive Wirtinger’s inequality and then applies it to a curve written in arc-length form to establish the result.

Hurwitz’s proof applies to smooth, closed curves that can be represented by piecewise $C^1$ (differentiable and has a continuous derivative), $2\pi$ -periodic functions whose derivatives are square-integrable. These assumptions are made to ensure that the tools and theorems we use later are valid. The Isoperimetric inequality itself, however, holds much more generally, even for curves that are not smooth, as proven in later geometrical proofs.

The purpose of this paper is to present a complete, step-by-step explanation of Hurwitz’s proof in a form that is understandable for advanced high-school students. The focus is the two-dimensional case and only the analytic method is developed. Other proofs and higher-dimensional versions are mentioned briefly for context but are not explored in detail. The paper begins with a short review of Fourier series, Parseval’s theorem, and Wirtinger’s inequality, followed by a simpler triangle case of the Isoperimetric inequality proved with the AM–GM inequality. It then presents the full Hurwitz proof and concludes with brief notes on generalizations and applications.

Methodology

Hurwitz’s proof of the Isoperimetric inequality utilizes $3$ important concepts: Fourier series, Parseval’s theorem, and Wirtinger’s inequality. The first two are applied to obtain Wirtinger’s inequality, which is used as a crucial step in the final proof.

Fourier Series

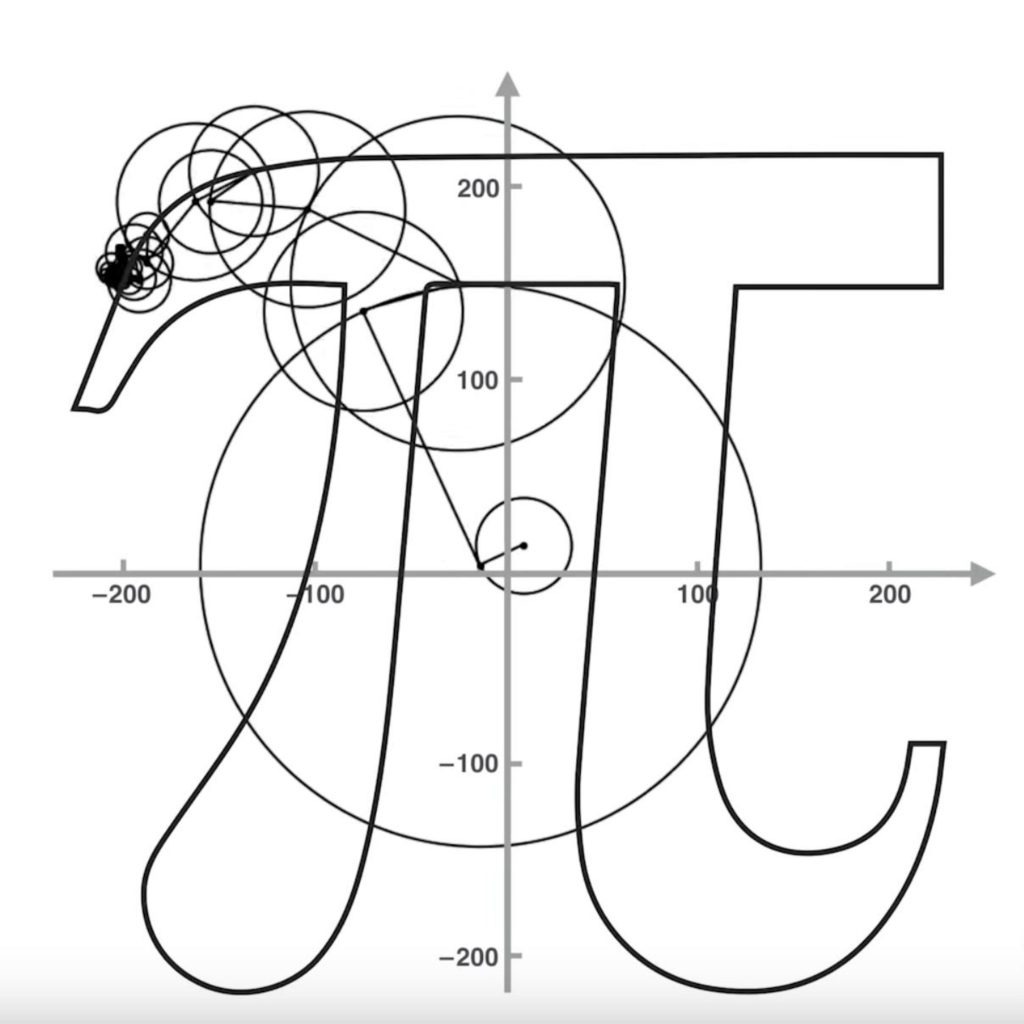
The Fourier series is a powerful tool to help approximate any function using only sine and cosine functions. The main idea is that it adds up a collection of waves made from a combination of sines and cosines to estimate the function. As the number of terms in the sum increases, the approximation gets finer and finer. When there are an infinite number of terms in the sequence, the sum is exactly equal to the function.⁴

The figure above shows how the sum of $3$ waves made of both sine and cosine functions can sum up to be the new wave. Remember that another way of representing sine and cosine waves are circles on complex planes with vectors rotating inside. Using the circles to lay out the Fourier Series we can see that it becomes a sequence of vectors connected tip to tail, each with a different radius and rotating at different frequencies. This chain of arrows can trace out anything in the $2$ dimensional complex plane with enough vectors.

Figure 2 | Fourier Series in the Complex Plane

While the Fourier series has many deeper properties, for the purpose of this paper we only need the general form of the series for most functions. For clarity, we assume throughout that $f$ is real-valued, $2\pi$ -periodic, piecewise $C^{1}$ on $[0,2\pi]$ , with $f,f'\in L^{2}(0,2\pi)$ . Under these hypotheses we can use mean-square convergence for Fourier series.

$f(x) = \frac{1}{2} a_0 + \sum_{n = 1}^{\infty}a_n\cos{(nx)} + \sum_{n = 1}^{\infty}b_n\sin{(nx)}$

Parseval’s Theorem

Parseval’s theorem⁵^‘⁶ states that if a function has a Fourier series

$f(x) = \frac{1}{2} a_0 + \sum_{n = 1}^{\infty}a_n\cos{(nx)} + \sum_{n = 1}^{\infty}b_n\sin{(nx)}$

then

$\frac{1}{\pi} \int_{-\pi}^{\pi} [f(x)]^2 dx = \frac{1}{2} a_0^2 + \sum_{n = 1}^{\infty} (a_n^2 + b_n^2)$

Parseval’s theorem holds for every $f\in L^{2}[-\pi,\pi]$ . In this paper Parseval is used in the mean-square sense, consistent with the mean-square convergence stated above.

Now we will prove the theorem. Squaring the Fourier series of $f(x)$ , we get

$[f(x)]^2 = \frac{1}{4} a_0^2 + a_0 \sum_{n = 1}^{\infty}[a_n\cos{(nx)} + b_n\sin{(nx)}] +$

$\sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty}[a_na_m\cos{(nx)}\cos{(mx)} +$

$a_nb_m\cos{(nx)}\sin{(mx)} +$

$a_mb_n\sin{(nx)}\cos{(mx)} +$

$b_nb_m\sin{(nx)}\sin{(mx)}]$

Taking the integral on both sides we get

$\int_{-\pi}^{\pi}[f(x)]^2dx = \frac{1}{4}a_0^2\int_{-\pi}^{\pi}dx +$

$a_0\int_{-\pi}^{\pi}\sum_{n = 1}^{\infty}[a_n\cos{(nx)} + b_n\sin{(nx)}]dx +$

$\int_{-\pi}^{\pi}\sum_{n = 1}^{\infty}\sum_{m = 1}^{\infty}[a_na_m\cos{(nx)}\cos{(mx)} +$

$a_nb_m\cos{(nx)}\sin{(mx)} +$

$a_mb_n\sin{(nx)}\cos{(mx)} +$

$b_nb_m\sin{(nx)}\sin{(mx)}]dx$

We will calculate each term separately. For the first term, we get

$\frac{1}{4}a_0^2\int_{-\pi}^{\pi}dx = \frac{1}{4}a_0^2(2\pi)$

For the second term, we notice that because sine and cosine are $2\pi$ periodic functions

$a_0\int_{-\pi}^{\pi}\sum_{n = 1}^{\infty}[a_n\cos{(nx)} + b_n\sin{(nx)}]dx = 0$

For the third term, we will use Orthogonality relations⁷. By Orthogonality relations, we can see that the following $3$ equations hold.

$\int_{-\pi}^{\pi}\cos{(nx)}\cos{(mx)}dx = \begin{cases} \text{$0$} & \text{if $n \neq m$} \\ \text{$\pi$} & \text{if $n = m \neq 0$} \\ \text{$2\pi$} & \text{if $n = m = 0$} \end{cases}$

$\int_{-\pi}^{\pi}\sin{(nx)}\sin{(mx)}dx = \begin{cases} \text{$0$} & \text{if $n \neq m$} \\ \text{$\pi$} & \text{if $n = m \neq 0$} \\ \text{$0$} & \text{if $n = m = 0$} \end{cases}$

$\int_{-\pi}^{\pi}\cos{(nx)}\sin{(mx)}dx = 0$

Plugging it into the third term, we get

$\sum_{n = 1}^{\infty}\sum_{m = 1}^{\infty}[a_na_m\pi\delta_{nm} + 0 + 0 + b_nb_m\pi\delta_{nm}]$

$\pi\sum_{n = 1}^{\infty}(a_n^2 + b_n^2)$

Notice that when we plug the Orthogonality relations in, we don’t have to worry about cases where $n = m = 0$ since $n \geq 1$ and $m \geq 1$ . Summing the $3$ terms together, we get

$\int_{-\pi}^{\pi}[f(x)]^2dx = \frac{1}{4}a_0^2(2\pi) + 0 + \pi\sum_{n = 1}^{\infty}(a_n^2 + b_n^2)$

So,

$\frac{1}{\pi} \int_{-\pi}^{\pi} [f(x)]^2 dx = \frac{1}{2} a_0^2 + \sum_{n = 1}^{\infty} (a_n^2 + b_n^2)$

Note that Parseval’s theorem is the equality case of Bessel’s inequality⁸.

Wirtinger’s Inequality

Wirtinger’s inequality⁹ says that let $f:\mathbb{R}\rightarrow\mathbb{R}$ be a periodic function of period $2\pi$ . The function is continuous and also has a continuous derivative throughout $\mathbb{R}$ . If

$\int_0^{2\pi}f(x) = 0$

then

$\int_0^{2\pi}f'(x)^2dx \geq \int_0^{2\pi}f(x)^2dx$

The equality case only holds when $f(x) = a\cos{x} + b\sin{x}$ for some $a$ and $b$ .

To prove it, we first see that because $f(x)$ is continuous, its derivative is continuous, and its period is $2\pi$ , Dirichlet’s conditions¹⁰ are met and we can write the Fourier series for $f(x)$ to be

$f(x) = \frac{1}{2}a_0 + \sum_{n = 1}^{\infty}(a_n\sin{(nx)} + b_n\cos{(nx)})$

Note that $a_0 = 0$ because

$\int_0^{2\pi}f(x) = 0$

Therefore, Parseval’s theorem now becomes

(1) $\begin{equation*} \frac{1}{\pi}\int_0^{2\pi}f(x)^2dx = \sum_{n = 1}^{\infty}(a_n^2 + b_n^2)\end{equation*}$

Note that we changed the parameters of the integral from $-\pi$ and $\pi$ to $0$ and $2\pi$ . This doesn’t change anything because $f(x)$ is a $2\pi$ periodic function. We can first take the derivative of $f(x)$ to get

$f'(x) = \sum_{n = 1}^{\infty}(a_nn\cos{(nx)} - b_nn\sin{(nx)})$

Plugging this into Parseval’s theorem gives us

(2) $\begin{equation*} \frac{1}{\pi}\int_0^{2\pi}f'(x)^2dx = \sum_{n = 1}^{\infty}n^2(a_n^2 + b_n^2)\end{equation*}$

Note that the minus sign in the equation for $f'(x)$ is canceled out due to squaring on the right-hand side of Parseval’s theorem. Because $n \geq 1$ , (2) $\geq$ (1), the Wirtinger’s inequality must be true.

Results

Isoperimetric Inequality on a Triangle

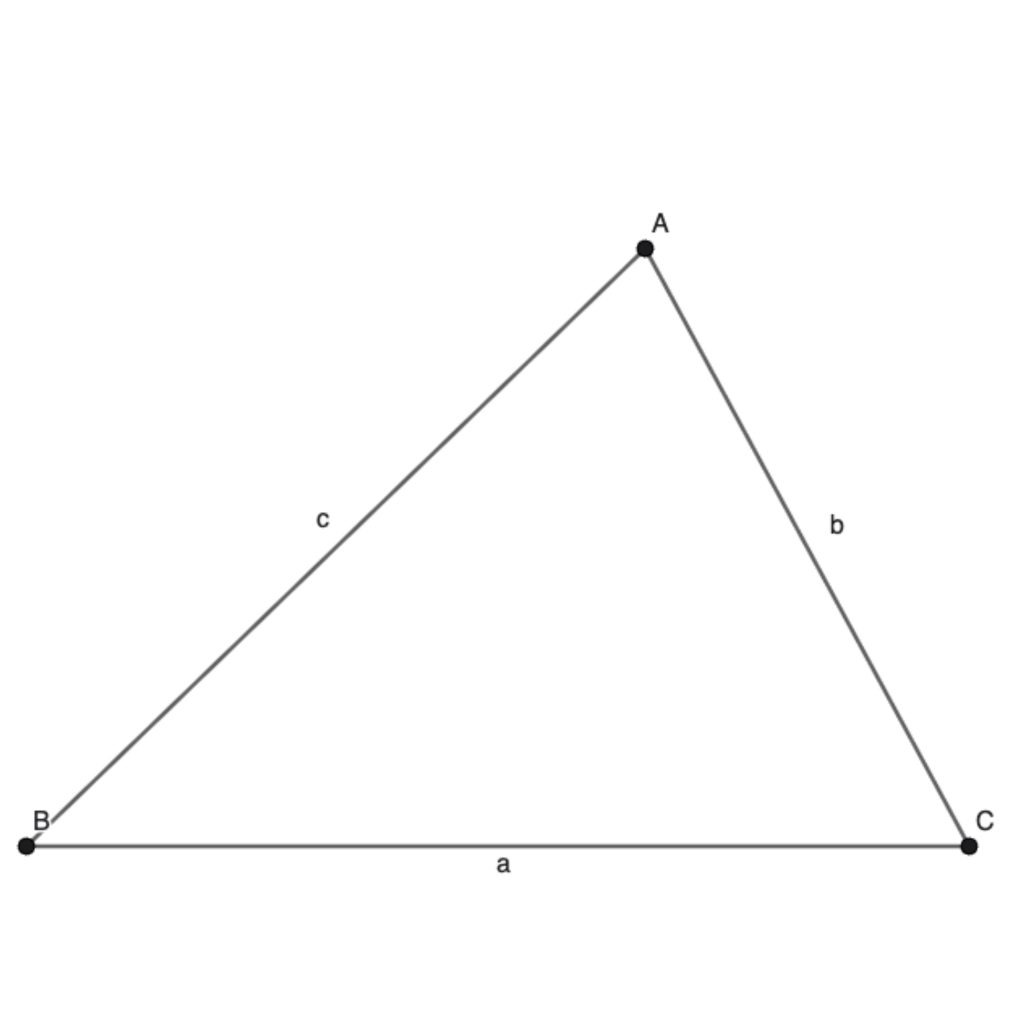
Let’s start things off with a simpler version of the problem. We will be proving the Isoperimetric inequality on a triangle.

The Isoperimetric inequality for triangles states that if L is the perimeter and A is the area

$L^2 \geq 12 \sqrt{3} \cdot A$

To prove this, we first need to prove AM-GM inequality.

AM-GM Inequality

The AM-GM inequality¹¹ states for all nonnegative reals $a_1,...,a_n$

$\frac{a_1 + ... + a_n}{n} \geq \sqrt[n]{a_1 \cdot ... \cdot a_n}$

The equality case holds when $a_i = a_j$ for all $i, j$ .

We will prove this via Cauchy induction. Cauchy induction is a form of the regular induction. In Cauchy induction, we first prove the base case, which is with 2 elements. Then we prove all the cases with $2^n$ elements. Finally, we prove that given $n$ elements work, $n - 1$ elements work.

The base case is the AM-GM inequality with 2 elements.

$\frac{x+y}{2} \geq \sqrt{xy}$

The more obvious and boring way to prove this is by doing some simple algebra.

$(x-y)^2 \geq 0$

$x^2 - 2xy + y^2 \geq 0$

$x^2 + 2xy + y^2 \geq 4xy$

$\frac{(x+y)^2}{4} \geq xy$

$\frac{x+y}{2} \geq \sqrt{xy}$

But we are here to have fun, so here is a much more interesting proof.

We set the circle to have diameter $x + y$ , where $\overline{CG}$ has length $x$ and $\overline{GB}$ has length $y$ . $\overline{AD}$ is perpendicular to $\overline{CB}$ and is the radius, so it has length $\frac{x+y}{2}$ . $\overline{EF}$ is perpendicular to $\overline{CB}$ which makes $\overline{EG} = \overline{GF}$ .

By using Power of a point on the chords $\overline{CB}$ and $\overline{EF}$ , we can see that $xy = \overline{EG} \cdot \overline{GF}$ . Thus, $\overline{EG} = \overline{GF} = \sqrt{xy}$ . We can see that by changing $x$ and $y$ , the position of the point $G$ on the line $\overline{CB}$ changes. However, no matter where $G$ is, $\overline{EG}$ will always be smaller than $\overline{AD}$ , which means $\frac{x+y}{2} \geq \sqrt{xy}$ .

Now that we are done with the base case, we want to take the first inductive step. Suppose AM-GM inequality works for $n$ elements. We want to prove that it works for $2n$ elements. Suppose that we have a list of $2n$ elements $a_1,...,a_{2n}$ . We can split this into two sequences of $n$ elements $a1,...,a_n$ and $a_{n + 1},...,a_{2n}$ . From this we can write two inequalities.

$\frac{x_1 + ... + x_n}{n} \geq \sqrt[n]{x_1...x_n}$

and

$\frac{x_{n + 1} + ... + x_{2n}}{n} \geq \sqrt[n]{x_{n+1}...x_{2n}}$

Now we add them and divide by $2$ .

$\frac{x_1 + ... + x_{2n}}{2n} \geq \frac{\sqrt[n]{x_1...x_n} + \sqrt[n]{x_{n + 1}...x_{2n}}}{2}$

Notice that now we can apply AM-GM inequality on the $2$ elements $\sqrt[n]{x_1...x_n}$ and $\sqrt[n]{x_{n + 1}...x_{2n}}$ to get

$\frac{\sqrt[n]{x_1...x_n} + \sqrt[n]{x_{n + 1}...x_{2n}}}{2} \geq \sqrt[2n]{x_1...x_{2n}}$

Which means that

$\frac{x_1 + ... + x_{2n}}{2n} \geq \sqrt[2n]{x_1...x_{2n}}$

Since the base case is $2$ elements, this proves AM-GM inequality for all powers of 2.

Now, we take the second inductive step. Assuming that AM-GM inequality works for $n$ elements, we must prove that it works for $n - 1$ elements. First, we substitute $x_n$ with $\frac{x_1 + ... + x_{n - 1}}{n - 1}$ . Plugging it in, we get

$\frac{x_1 + ... + x_{n - 1} + \frac{x_1 + ... + x_{n - 1}}{n - 1}}{n} \geq \sqrt[n]{x_1...x_{n - 1}\left(\frac{x_1 + ... + x_{n - 1}}{n - 1}\right)}$

Note that because we assumed the inequality to be true with $n$ elements, equality must hold if and only if $x_1 = x_2 = ... = x_{n - 1} = \frac{x_1 + ... + x_{n - 1}}{n - 1}$ . However, notice that if $x_1 = x_2 = ... = x_{n - 1}$ , $\frac{x_1 + ... + x_{n - 1}}{n - 1}$ must be equal as well. So, the equality case holds if and only if $x_1 = x_2 = ... = x_{n - 1}$ .

We can now continue by multiplying $n - 1$ to the numerator and the denominator of the left-hand side.

$\frac{x_1 + ... + x_{n - 1} + \frac{x_1 + ... + x_{n - 1}}{n - 1}}{n} = \frac{nx_1 + ... + nx_{n - 1}}{n(n - 1)} = \frac{x_1 + ... + x_{n - 1}}{n - 1}$

Plugging it back in, we get

$\frac{x_1 + ... + x_{n - 1}}{n - 1} \geq \sqrt[n]{x_1...x_{n - 1}\left(\frac{x_1 + ... + x_{n - 1}}{n - 1}\right)}$

$\left(\frac{x_1 + ... + x_{n - 1}}{n - 1}\right)^n \geq x_1...x_{n - 1}\left(\frac{x_1 + ... + x_{n - 1}}{n - 1}\right)$

$\left(\frac{x_1 + ... + x_{n - 1}}{n - 1}\right)^{n - 1} \geq x_1...x_{n - 1}$

$\frac{x_1 + ... + x_{n - 1}}{n - 1} \geq \sqrt[n - 1]{x_1...x_{n - 1}}$

Thus, by Cauchy induction, we have proved AM-GM inequality.

Proving the Triangle Case

First, we will define $s = \frac{a + b + c}{2}$ . Now, we will apply AM-GM inequality on the $3$ terms $(s - a)$ , $(s - b)$ , and $(s - c)$ to get

$\frac{(s - a) + (s - b) + (s - c)}{3} \geq \sqrt[3]{(s - a)(s - b)(s - c)}$

$\frac{s}{3} \geq \sqrt[3]{(s - a)(s - b)(s - c)}$

$\frac{s^3}{27} \geq (s - a)(s - b)(s - c)$

Using Heron’s formula, we get

$\frac{s^4}{27} \geq A^2$

$s^2 \geq 3\sqrt{3} \cdot A$

$L^2 \geq 12\sqrt{3} \cdot A$

Adolf Hurwitz’s Proof of the Isoperimetric Inequality

The main idea for this proof is that it calculates the area of the shape, and compares it to another quantity using Wirtinger’s inequality. The other quantity is cleverly set up so that the result directly gives us the Isoperimetric inequality. We first parameterize the curve by arc length and then rescale to make it $2\pi$ -periodic so that Fourier methods apply.

Lemma (Translation invariance and normalization)

Let $\gamma:[0,L]\to\mathbb{R}^{2}$ , $s\mapsto(x(s),y(s))$ , be a simple closed $C^1$ curve parametrized by arc length. If we shift the entire curve by a fixed vector $(x_0,y_0)$ , the perimeter and enclosed area do not change. Indeed,

$L = \int_0^L\sqrt{x'(s)^2 + y'(s)^2}ds$

depends only on derivatives, so adding constants has no effect. For the area,

$A = \frac{1}{2}\int_0^L(x(s)y'(s) - y(s)x'(s))ds$

the shift adds $\frac{1}{2}\int_0^L(x_0y'(s) - y_0x'(s))ds = \frac{1}{2}(x_0(y(L) - y(0)) - y_0(x(L) - x(0))) = 0$ , because the curve is closed. Therefore translation leaves $L$ and $A$ unchanged. After we later rescale to periodic functions $(f(\theta),g(\theta))$ with $\theta\in[0,2\pi]$ , we may translate so that

$\int_0^{2\pi}f(\theta)d\theta = 0$

Parameterizing by Arc Length

We start off by noticing that we can represent the closed curve using $2$ piecewise functions $x(s)$ and $y(s)$ where $s \in [0, L]$ that satisfy

(3) $\begin{equation*} \left(\frac{dx}{ds}\right)^2 + \left(\frac{dy}{ds}\right)^2 = 1\end{equation*}$

We can make this assumption because this is what it means to parameterize by arc length. It essentially limits how much you go around the perimeter in each step to $1$ . We can think of this as a “speed” of $1$ .

Working with a curve defined by arc length allows us to fix the total perimeter while keeping the description smooth and continuous. To apply Fourier series conveniently, we now rescale this parameterization so that the functions repeat every $2\pi$ .

Rescaling to $2\pi$ Periodicity

Because the functions $x(s)$ and $y(s)$ are $L$ periodic (the perimeter is a closed curve of length $L$ ), we can make new functions $f(\theta)$ and $g(\theta)$ to be functions of $x(s)$ and $y(s)$ so that they are $2\pi$ periodic, where $\theta \in [0, 2\pi]$ .

$f(\theta) = x\left(\frac{L\theta}{2\pi}\right)$

$g(\theta) = y\left(\frac{L\theta}{2\pi}\right)$

We will also define

$s = \frac{L\theta}{2\pi}$

Notice that we have the ability to shift the shape around the plane since it does not affect the inequality in any way. So, for later convenience, we will shift the graph so that $\int_0^{2\pi}f(\theta)d\theta = 0$ . Now, we can take the derivative $\frac{d}{d\theta}$ and plug it back into (3). Using the chain rule, we get

$f'(\theta) = x'\left(\frac{L\theta}{2\pi}\right) \cdot \frac{L}{2\pi}$

$g'(\theta) = y'\left(\frac{L\theta}{2\pi}\right) \cdot \frac{L}{2\pi}$

So,

$(f'(\theta))^2 + (g'(\theta))^2 = \left[\left(x'\left(\frac{L\theta}{2\pi}\right)\right)^2 + \left(y'\left(\frac{L\theta}{2\pi}\right)\right)^2\right] \cdot \left(\frac{L}{2\pi}\right)^2$

But because of (3), everything inside the square brackets equals to $1$ .

(4) $\begin{equation*} (f'(\theta))^2+(g'(\theta))^2 = \frac{L^2}{4\pi^2}\end{equation*}$

Now that $f(\theta)$ and $g(\theta)$ are $2\pi$ -periodic, we can express the enclosed area in terms of these functions. Computing the area is the next step toward $L^2 \ge 4\pi A$ , since the inequality relates perimeter to area.

Writing the Area Integral in Terms of $f$ and $g$

Recall that the formula for the area enclosed by a curve is¹²^‘¹³

(5) $\begin{equation*} A = \frac{1}{2}\int_0^L(x(s)y'(s) - y(s)x'(s))ds\end{equation*}$

This is similar to how the determinant of a matrix calculates the area of the shape it represents. In fact, the area of a triangle can be calculated by multiplying $\frac{1}{2}$ to the determinant of the matrix, similar to the equation above. Now we need to define and calculate a few conditions that we will use later. Because

$s = \frac{L\theta}{2\pi}$

the following conditions hold.

$ds = \frac{L}{2\pi}d\theta$

$x(s) = f(\theta)$

$y(s) = g(\theta)$

Now we need to calculate what $f'(\theta)$ and $g'(\theta)$ are.

$f(\theta) = x\left(\frac{L\theta}{2\pi}\right)$

By the chain rule,

$f'(\theta) = x'\left(\frac{L\theta}{2\pi}\right) \cdot \frac{L}{2\pi}$

$x'(s) = \frac{2\pi}{L} \cdot f'(\theta)$

Similarly,

$y'(s) = \frac{2\pi}{L} \cdot g'(\theta)$

Now, substituting everything back into (5) we get

$A = \frac{1}{2}\int_0^{2\pi}\left(\frac{2\pi}{L}f(\theta)g'(\theta) - \frac{2\pi}{L}g(\theta)f'(\theta)\right)\frac{L}{2\pi}d\theta$

(6) $\begin{equation*} 2A = \int_0^{2\pi}(f(\theta)g'(\theta) - g(\theta)f'(\theta))d\theta\end{equation*}$

We now use integration by parts. The formula for integration by parts comes from the product rule $(uv)' = u'v + uv'$ . Integrating on both sides gives us $[uv + C] = \int{u'v} + \int{uv'}$ where $C$ is the constant after integrating. Rearranging the equation results in $\int{uv'} = [uv + C] - \int{u'v}$ . Since this equation works on a definite interval, the $C$ in $[uv + C]$ will cancel out no matter what, so we can just remove it to get $\int{uv'} = [uv] - \int{u'v}$ . Plugging in $u = f(\theta)$ and $v = g(\theta)$ , we get

$\int_0^{2\pi}f(\theta)g'(\theta)d\theta = [f(\theta)g(\theta)]_0^{2\pi} - \int_0^{2\pi}g(\theta)f'(\theta)d\theta$

Since $f(\theta)$ and $g(\theta)$ are $2\pi$ periodic functions,

$f(0) = f(2\pi)$

and

$g(0) = g(2\pi)$

Then,

$[f(\theta)g(\theta)]_0^{2\pi} = f(2\pi)g(2\pi) - f(0)g(0) = 0$

So,

$\int_0^{2\pi}f(\theta)g'(\theta)d\theta = - \int_0^{2\pi}g(\theta)f'(\theta)d\theta$

Returning back to (6) we can rewrite it into this.

(7) $\begin{equation*} 2A = 2\int_0^{2\pi}f(\theta)g'(\theta)d\theta\end{equation*}$

Our next goal is to rewrite the area integral into a form that can be directly compared with an integral involving the derivatives of $f$ and $g$ because the perimeter can be directly represented by them as mentioned in (4).

Reorganizing the Equation

We can complete the square so that (7) becomes

$2A = \int_0^{2\pi}(f(\theta)^2 + g'(\theta)^2 - (f(\theta) - g'(\theta))^2)d\theta$

Because the last term is non-negative,

$2A \leq \int_0^{2\pi}(f(\theta)^2 + g'(\theta)^2)d\theta$

At this point, we can use Wirtinger’s inequality to relate the integral of $f(\theta)^2$ to that of $f'(\theta)^2$ . This step is essential because it converts the geometric problem into an analytic inequality involving derivatives. By the lemma at the start of the proof, we may assume $\int_0^{2\pi}f(\theta)d\theta = 0$ , so we apply Wirtinger’s inequality to $f$ alone, which means that no condition on $g$ is needed. Remember that Wirtinger’s inequality states that

$\int_0^{2\pi}f(\theta)^2d\theta \leq \int_0^{2\pi}f'(\theta)^2d\theta$

It follows that

$\int_0^{2\pi}(f(\theta)^2 + g'(\theta)^2)d\theta \leq \int_0^{2\pi}(f'(\theta)^2 + g'(\theta)^2)d\theta$

So,

$2A \leq \int_0^{2\pi}(f'(\theta)^2 + g'(\theta)^2)d\theta$

We have now related the area to $f'(\theta)$ and $g'(\theta)$ , so we use (4), which links these derivatives to the fixed perimeter $L$ . Substituting (4) on the right hand side gives

$2A \leq \int_0^{2\pi}\frac{L^2}{4\pi^2}d\theta = \frac{L^2}{4\pi^2} \cdot 2\pi = \frac{L^2}{2\pi}$

Rearranging the equation gives us the Isoperimetric inequality.

$L^2 \geq 4\pi A$

If equality holds in the Isoperimetric inequality, then every step above must also be an equality. The complete the square step forces $\int_0^{2\pi}(f(\theta) - g'(\theta))^2d\theta = 0$ when there is an equality. Since the integral of a non-negative quantity is equal to $0$ when that quantity is $0$ , we get that $f(\theta) = g'(\theta)$ .

From Wirtinger’s inequality, equality happens only when the Fourier series of $f$ contains the first sine–cosine terms and no higher frequencies. This is called Fourier coefficient localization at $n = 1$ . In this case, $f(\theta) = a\cos{\theta} + b\sin{\theta}$ . Integrating on $f(\theta) = g'(\theta)$ tells us that $g(\theta) = a\sin{\theta} - b\cos{\theta} + C$ . Together, these functions $(f(\theta), g(\theta))$ trace a circle of radius $\frac{L}{2\pi}$ , meaning that equality holds for the Isoperimetric inequality when the curve is a circle.

Generalization

The first step one should take after proving something is to attempt to generalize. We will not be able to prove these generalizations as they are outside the scope of this paper, but we will cover the ideas of how they work. The usual Isoperimetric inequality works on a $2$ dimensional plane. The natural move is to generalize to more dimensions. For example, in $3$ dimensional space, the inequality would relate the surface area to the volume of an object. It turns out that it is possible to generalize to any higher dimension¹⁴, but it is extremely complex.

Another way of generalizing the inequality is to do it in different spaces.

Figure 5 | Isoperimetric Inequality on a Sphere

For example, on a sphere, the Isoperimetric inequality becomes

$L^2 \geq 4 \pi A - \frac{A^2}{R^2}$

where R is the radius of the sphere. Other generalizations include the Isoperimetric inequality in Hadamard Manifolds and in metric measure spaces.

Applications

This section presents several concrete uses of the isoperimetric principle. We first give two geometric examples that follow directly from $L^{2}\ge 4\pi A$ , namely the maximal area with a straight shoreline and an area bound for curves of constant width using $L=\pi w$ . We then include an advanced example, Cheeger’s inequality, which links a geometric isoperimetric ratio to the rate at which heat or vibrations even out in a region. Full background from partial differential equations is not required here. The key point is that the same boundary-area tradeoff that makes circles optimal in the Isoperimetric inequality also limits diffusion in analytic settings.

Dido’s Problem

Dido’s problem asks for the maximum area that can be enclosed by a line of a fixed length, given that a straight coastline forms the remainder of the boundary.

Let the boundary that isn’t the coastline be an arc of length $L$ . Reflect the region across the line. The reflected shape is a closed region with perimeter $2L$ and area $2A$ . By the Isoperimetric inequality,

$(2L)^2 \geq 4\pi(2A)$

$L^2 \geq 4\pi\left(\frac{A}{2}\right)$

Equality holds exactly when the doubled region is a circle, so the original region is a semicircle whose arc length is $L$ .

Curves of Constant Width

Let a convex plane curve have constant width $w$ . Barbier’s theorem¹⁵ gives the exact perimeter $L = \pi w$ . Substituting into $L^2 \geq 4\pi A$ gives us

$A \leq \frac{L^2}{4\pi} = \frac{\pi w^2}{4}$

with equality only for the circle of diameter $w$ . This quantifies how far any constant width shape is from the optimal area for its fixed width.¹⁶

Cheeger’s inequality

The Isoperimetric inequality has many extensions beyond geometry. One deep example appears in mathematical physics and analysis, known as Cheeger’s inequality. This result connects the shape of a region to how quickly heat or energy spreads inside it.

Without going into full technical detail, we can describe the main idea. For a region $\Omega$ in the plane, the Cheeger constant $h(\Omega)$ measures how easily the region can be divided into two parts compared to its boundary length. A region with a narrow “neck” has a small $h(\Omega)$ , while a compact, round region has a large one. Meanwhile, the first nonzero eigenvalue $\lambda_1$ of the Laplacian, a differential operator that models heat flow, measures how fast heat or vibrations even out in $\Omega$ .

Cheeger’s inequality states that

$\lambda_1 \geq \frac{h(\Omega)^2}{4}$

This means that regions which are close to being isoperimetric (large $h(\Omega)$ , like circles) allow faster diffusion or vibration, while regions with thin bottlenecks (small $h(\Omega)$ ) slow it down. Although this connection involves advanced ideas such as eigenvalues and differential operators, it shows that the same geometric principle behind the Isoperimetric inequality also governs how shapes behave in physics and analysis.¹⁷

Discussion

Hurwitz’s proof shows that algebra and analysis can be used to solve what first looks like a geometry problem. Instead of working with shapes directly, the proof rewrites the boundary as functions and then analyzes those functions using Fourier series. This makes the argument more general and shows how inequalities in analysis can describe geometric ideas. Compared with older geometric proofs, Hurwitz’s method is appealing because every step follows from clear algebraic or analytic reasoning.

The approach also connects the Isoperimetric inequality to many areas of modern mathematics, like Fourier analysis, calculus of variations, and spectral geometry. These connections show that the same ideas behind a simple shape problem can also describe how heat spreads, how waves move, or how space itself behaves in higher dimensions. Overall, Hurwitz’s proof gives an elegant and understandable way to see one of the oldest mathematical inequalities through the lens of modern analysis.

Conclusion

Throughout this paper, we studied the Isoperimetric inequality from both a historical and mathematical point of view. We began with the story of Queen Dido and the founding of Carthage, then reviewed the main tools used in the proof, such as Fourier series, Parseval’s theorem, Wirtinger’s inequality, and the AM–GM inequality. After proving a simpler version for triangles, we went through Hurwitz’s full analytic proof step by step and looked at a few generalizations and applications.

Hurwitz’s approach is interesting because it turns a geometric problem into one that can be solved with algebra and calculus. Instead of using geometric constructions, the proof represents the curve with periodic functions and studies them using Fourier analysis. Parseval’s theorem connects the geometry of the curve to these functions, and Wirtinger’s inequality provides the final comparison needed for the result.

This analytic method is clear, logical, and easier to follow than most other proofs once the main ideas are known. It also explains why the circle is the only shape that achieves equality in the inequality. Hurwitz’s proof shows that even an old geometric question can be understood in a new way by combining simple analytic ideas together.

Acknowledgments

I would like to acknowledge Zarif Ahsan for his guidance throughout writing this paper. Thanks to Simon Rubinstein-Salzedo of the Euler Circle for providing the opportunity for independent research for the summer.

References

R. Osserman. The isoperimetric inequality. Bull. Amer. Math. Soc. 84(6), 1182–1238 (1978). [↩]
E. Hoisington. An exposition of Hurwitz’s isoperimetric method. arXiv preprint arXiv:1909.06347 (2019). [↩]
A. Treibergs. Mixed area and the isoperimetric inequality (2009). https://www.math.utah.edu/~treiberg/MixedAreaSlides.pdf [↩]
R. Perumal, R. Gopal, and R. Selvakumar. “A study about Fourier series: Mathematical and graphical models and application in electric current and square oscillations.” ResearchGate (2021). https://www.researchgate.net/publication/350973707 [↩]
W. Kaplan. Advanced Calculus, 4th ed. Addison-Wesley Publishing Company, Reading, MA (1991), p. 519. [↩]
E. W. Weisstein. Parseval’s theorem. MathWorld (Wolfram). https://mathworld.wolfram.com/ParsevalsTheorem.html [↩]
MIT OpenCourseWare. Orthogonality relations (2011). https://ocw.mit.edu/courses/18-03sc-differential-equations-fall-2011/ [↩]
S. S. Dragomir. “Bessel’s inequality and its extensions in inner product spaces.” Journal of Mathematical Analysis and Applications 329(2), 1311–1320 (2007). [↩]
W. E. Milne. “Integral inequalities of the Wirtinger type.” Duke Mathematical Journal 25(3), 459–464 (1958). [↩]
P. Singh, A. Singhal, B. Fatimah, A. Gupta, and S. D. Joshi. “Proper definitions and demonstration of Dirichlet conditions.” TechRxiv preprint (2021). https://www.techrxiv.org/doi/full/10.36227/techrxiv.14761539.v1 [↩]
M. D. Hirschhorn. “The AM–GM inequality.” The Mathematical Intelligencer 29(4), 7 (2007). DOI:10.1007/BF02986168. [↩]
R. F. Muirhead. “A proof of Green’s theorem and its application to area computation.” The Mathematical Gazette 66(437), 105–107 (1982). [↩]
D. Q. Nykamp. Using Green’s theorem to find area. Math Insight. https://mathinsight.org/greens_theorem_find_area [↩]
X. Cabré. “Isoperimetric, Sobolev, and eigenvalue inequalities via the Alexandroff–Bakelman–Pucci method: A survey.” Chinese Annals of Mathematics, Series B 38(1), 1–14 (2017). [↩]
P. J. Davis. “Barbier’s Theorem and Curves of Constant Width.” In Ingenuity in Mathematics, pp. 157–164. The Mathematical Association of America, Washington, D.C. (1979). [↩]
B. Kawohl, G. Sweers. On a formula for sets of constant width in 2D. Communications in Pure and Applied Analysis 18(6), 2825–2837 (2019). [↩]
J. Cheeger. A lower bound for the smallest eigenvalue of the Laplacian. In Problems in Analysis, 195–199. Princeton University Press, Princeton, NJ (1970). [↩]

Isoperimetric Inequality

Abstract

Introduction

Methodology

Fourier Series

Parseval’s Theorem

Wirtinger’s Inequality

Results

Isoperimetric Inequality on a Triangle

AM-GM Inequality

Proving the Triangle Case

Adolf Hurwitz’s Proof of the Isoperimetric Inequality

Lemma (Translation invariance and normalization)

Parameterizing by Arc Length

Rescaling to $2\pi$ Periodicity

Writing the Area Integral in Terms of $f$ and $g$

Reorganizing the Equation

Generalization

Applications

Dido’s Problem

Curves of Constant Width

Cheeger’s inequality

Discussion

Conclusion

Acknowledgments

References

LEAVE A REPLY Cancel reply

POPULAR CATEGORIES

NAVIGATION

ABOUT US

Abstract

Introduction

Methodology

Fourier Series

Parseval’s Theorem

Wirtinger’s Inequality

Results

Isoperimetric Inequality on a Triangle

AM-GM Inequality

Proving the Triangle Case

Adolf Hurwitz’s Proof of the Isoperimetric Inequality

Lemma (Translation invariance and normalization)

Parameterizing by Arc Length

Rescaling to Periodicity

Writing the Area Integral in Terms of and

Reorganizing the Equation

Generalization

Applications

Dido’s Problem

Curves of Constant Width

Cheeger’s inequality

Discussion

Conclusion

Acknowledgments

References

RELATED ARTICLESMORE FROM AUTHOR

The Effect of Piped-in Music and Preferred Music on Focus in Adolescents with Type A and Type B Personalities

Genetic Neural Network Architecture Optimization: A Hybrid Evolutionary and Bayesian Approach

Unlocking AI’s Potential in China’s Healthcare System: Overcoming Structural and Economic Barriers

LEAVE A REPLY Cancel reply

POPULAR CATEGORIES

NAVIGATION

ABOUT US

Rescaling to $2\pi$ Periodicity

Writing the Area Integral in Terms of $f$ and $g$

RELATED ARTICLES MORE FROM AUTHOR