Word Finiteness Problem

By
Bocharov Maksim Andreevich
-
0
453
Read the full article as a PDFDownload

Abstract

Computability Theory investigates what can be solved by algorithms for a finite number of iterations and what can not, helping to estimate the boundaries of computational possibilities. This research analyses the set finiteness problem, which determines whether a problem of determining that a set of words equal to a particular word generated on certain conditions is finite or infinite, decidable or undecidable. The idea of research is to prove the undecidability of the problem that afterward may be used in coming up with a more clear understanding of a decidable version of Word Problem. The method of proof is to step-by-step reduce the investigated problem to other ones, the last one of which is known to be undecidable. The result showed that such a ‘chain’ of valid steps exists, which means that the assumption about undecidability was correct. Furthermore, because we used the method of ‘chain’, many other nontrivial problems appeared to be undecidable, making the research even more productive for understanding the known boundaries of computational possibilities.
Keywords: Computability theory, group theory, undecidability, decidability, halting problem.

1. Definitions and theorems.

First of all, it’s necessary to involve some definitions from computability theory.

Word1

Let’s determine the combination of symbols from the finitely presented semigroup as a word.

Quadruple1

Quadruple is a 4‑tuple of one of the following 3 types:

q_i s_j s_m q_l
q_i s_j R q_l
q_i s_j L q_l

Turing machine (Formal definition, from)1

Turing machine consists of:

  1. A finite set S is called the alphabet of the Turing machine whose elements we call symbols. These symbols are possible things that can be written on each tape cell of the Turing machine. The alphabet includes a distinguished blank symbol that we denote \sqcup.
  2. A finite set Q of states, one of which is distinguished as the starting state and the other as the halting state.
  3. A partial function
    [ t: S \times Q ; \to ; S \times Q \times {L,R} ]
    called the transition map: if we are in state~q, the current cell contains the symbol~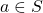a\in S, and
    (t(a,q)=(a’,q’,X)),
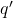    then the machine writes a' in the current cell, moves to state~q', and shifts the tape one cell in direction~X\in{L,R}.

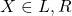    Instantaneous description1
    An instantaneous description \alpha is a positive word of the form
    \alpha = \sigma q_1 \tau, where \sigma and \tau are s‑words
    and \tau is not empty.

h-special word
Let w be a word on semigroup C, then w is h‑special, if
w = h\,w'\,h, where w' is an instantaneous description.

Input instantaneous description1

Let’s determine an instantaneous description of a particular Turing machine,
which it starts with as an input instantaneous description.

Halting instantaneous description1

Let’s determine an instantaneous description of a particular Turing machine,
which it ends with as a halting instantaneous description.

Basic move

Let T be a Turing machine, A and B are instantaneous descriptions. Then there is a basic move from A to B if one of the following conditions is satisfied:

A = u q_i s_j u' and B = u q_l s_k u', where q_i s_j s_k q_l \in T;
A = u q_i s_j s_k u' and B = u s_j q_l s_k u', where q_i s_j R q_l \in T;
A = u q_i s_j and B = u s_j q_l s_0, where q_i s_j R q_l \in T;
A = u s_k q_i s_j u' and B = u q_l s_k s_j u', where q_i s_j L q_l \in T;
A = q_i s_j u' and B = q_l s_0 s_k u', where q_i s_j L q_l \in T.

Where u and u' are s words (possibly empty).

Set J

J = {(C,S)\mid \text{there are only finitely many words }S'\text{ of } C \text{ equal to }S}
\times{\text{finitely presented semigroups}} \times {\text{words}}.

In other words, J is the set of all such pairs (C,S), where C is a finitely presented semigroup and S is one of its elements, and there are only finitely many other elements of C equal to S.

Set W

W = {(T,R) \mid \text{there are only finitely many instantaneous}
\text{descriptions } B \text{ of } T \text{ that eventually reach } R
\text{and for each such } B \text{ there is some input}
\text{instantaneous description } B' \text{ that eventually reaches } B}
\times {\text{Turing machines}} \times {\text{instantaneous descriptions}}.

In other words, (W) is a set of such pairs (T, R), where (T) is a particular Turing machine and (R) is a particular instantaneous description of (T) and there are finitely many such instantaneous description (B) of (T) that eventually get to (R) and for any (B) there is some input instantaneous description (B’) that eventually gets to (B).

Set V

    \[ \begin{aligned}V = \{T \mid\ &\text{there are only finitely many inputs} \text{on which } T \text{ halts} \} ; \{\text{Turing machines}\}.\end{aligned} \]

In other words, (V) is the set of all Turing machines that halt on finitely many inputs.

2. Introduction

Nowadays, computer science develops rapidly, hence it’s crucial to understand the solvability of problems. Computability theory explores the limitations of what problems can be and cannot be solved algorithmically. The Halting problem, which determines whether a given Turing machine will eventually halt or continue running indefinitely for any given input and which was proved to be undecidable by Alan Turing in 1936, is a crucial problem in computability theory, which led to determining the decidability of many other problems in this sphere.

In this paper we will explore the question “if there is given a finitely presented semigroup (G = \langle l_1, l_2, \dots, l_m \mid r_1, r_2, \dots, r_n\rangle), a word (w) on the generators (l_1, \dots, l_m), is the problem of determining whether the set of words (w’) (such that (w’) is a word on the generators (l_1, \dots , l_m) and (w’=w) in (G)) is finite or infinite, decidable or undecidable?” Let’s say that is the Word Finiteness problem. Let’s proceed with the structure of the proof.

3. Methods

The general idea of the proof is that we will step by step reduce our initial problem to other problems, where the last one in a chain will be the undecidable problem.

Here are the crucial steps of the structure of the research:

Build a list of relations for a computable function (G(T)), which takes as input a particular Turing machine (T) and builds a finitely presented semigroup, which helps us to represent steps of (T) by combinations of symbols in the semigroups.
State an Instantaneous Descriptions problem.
Prove that the undecidability of the Instantaneous Descriptions problem leads to the undecidability of the Word Finiteness problem.
State an Input Finiteness problem.
Prove that the undecidability of the Input Finiteness problem leads to the undecidability of the Instantaneous Descriptions problem.
Prove that the Input Finiteness problem is undecidable by reducing it to the Halting problem.

4. Function G from Turing machines to finitely presented semigroups.

In Rotman, the authors proved that the question of a finitely presented semigroup being trivial is undecidable by encoding Turing machines in terms of semigroups. We will follow a similar technique, but add some extra relations that are necessary for our proof.

List of relations

If (T) is a given Turing machine, then the semigroup (G(T)) has the presentation

[G(T) \;=\;\bigl\langle h,\,s_1,\,s_2,\dots,s_m,\,q_1,\,q_2,\dots,q_n \;\bigm|\; R(T)\bigr\rangle,]

where (R(T)) is the following set of relations:

(q_i s_j = q_l s_k \text{if} \quad q_i s_j s_k q_l \in T)}
(q_i s_j s_B = s_j q_l s_B) \text{if} \quad (q_i s_j R q_l \in T),
(q_i s_j h = s_j q_l s_0 h) \text{if} \quad (q_i s_j R q_l \in T),
(s_B q_i s_j = q_l s_B s_j) \text{if} \quad (q_i s_j L q_l \in T),
(h q_i s_j = h q_l s_0 s_j) \text{if} \quad (q_i s_j L q_l \in T),
(s_j q_l s_0 h = q_i s_j h) \text{if} \quad (q_l s_0 L q_i \in T),
b(h q_l s_0 s_j = h q_l s_j q_i) \text{if} \quad (q_l s_0 R q_i \in T).

This function allows us to operate with Turing machines in the language of semigroups.

5. Instantaneous Descriptions Problem

If we have a pair (T,R) \in {\text{Turing machines}} \times {\text{instantaneous descriptions}}, is the problem of determining whether (T,R) belongs to (W) or is it not decidable or undecidable?

6. Proof that instantaneous description problem is equal to the Word Finiteness problem

Want to show that if we have a pair (T,R) where R is a halting instantaneous description with at most one s_0 on either end, and
[ L'(T,R) = (S,w), ]
then the set of instantaneous descriptions of T that eventually get to R is finite if and only if the set of words equal to w in S is finite.

    \[ A(R) = \left{ \begin{aligned}&\text{instantaneous descriptions } R' \text{ with at most one } s_0 \\&\text{on either end, that eventually get to} R \end{aligned} \right}.\]

    \[ B(w) = \left{ \begin{aligned}& \text{words } w' \text{ on the generators of } G(T) \\& \text{that are equal to } w \text{ in } G(T) \end{aligned} \right}.\]

Want to show for R a halting instantaneous description with at most one s_0 at either end that A(R) is finite if and only if B(hRh) is finite.

If R' is an instantaneous description that eventually gets to R, then hR'h is a word on the generator of G(T) which is equal to w, which means that if A(R) is infinite, then B(hRh) is also infinite.

If we have an element hR'h of B(hRh), then R' is an element of A(R), this will prove that if the set B(hRh) is infinite then A(R) is also infinite, satisfying the condition of if and only if.

First, we should note that since our relations preserve h–letters, each word w_j in the chain
hR'h \;\to\; w_1 \;\to\; w_2 \;\to\; \dots \;\to\; w_t \;\to\; hRh
is h-special. Hence, each

w_j = h\,r_j\,h

where r_j is an instantaneous description. We know that either
r_j \;\xrightarrow{1} ; r_{j+1} \text{or} r_{j+1} \;\xrightarrow{1} ; r_j
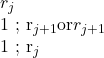
is a basic move of T, since w_j \to w_{j+1} is an elementary operation of one of the first five types (see, Lemma 12.3(ii), p. 427).

Let us prove by induction that in our chain of steps all the arrows go to the right. It will follow that R' will eventually reach R, which means that R' belongs to A(R). It is clear that the last arrow cannot be left-looking, because hRh is terminal, so w_t \gets hRh cannot occur; hence in our chain there is at least one right-looking arrow. This shows that for a chain of two elements all arrows are right-going, proving the base case for t=2, where t is the number of elements (words w_i = hrh) in the chain. Let’s find a place where

r_{i-1} \;\gets\; r_i \;\to\; r_{i+1},

otherwise if there is no such place, all the arrows are going to the right (version of Lemma 12.4 from, pp. 427–428)

Once we find such a place, from which we can determine that r_{i-1} = r_{i+1} (because there is never ambiguity about the next step of a Turing machine, i.e., from r_i we cannot get two different instantaneous descriptions), we can remove r_i and r_{i+1} and connect r_{i-1} to r_{i+2} directly. This reduces our chain length by 2, and by the induction hypothesis all shorter chains are right-going, so the original chain is right-going as well.

Therefore, all arrows are on the right, all r_j are instantaneous descriptions with at most one s_0 on either end, and hence R' is also such a description, proving that R'\in A(R) and completing the if-and-only-if proof.

7. Input Finiteness problem

If we have a T in {\text{Turing machines}}, is the problem of determining whether T \in V or not decidable or undecidable?

8. Proof that the problem of instantaneous descriptions is equivalent to the Input Finiteness problem

We want
M \colon {\text{Turing machines}} \longrightarrow\; {\text{Turing machines}} \times {\text{instantaneous descriptions}}

such that M(T)\in W if and only if T\in V. The existence of such a function M shows that if the Input Finiteness problem is decidable, then by computing M(T)=(T',R) we can decide membership in~W. In particular, T\in V when (T',R)\in W and vice versa.

Let us define a helper function
M' \colon {\text{Turing machines}} ; \longrightarrow ; {\text{Turing machines}}.
On input a machine T, M' outputs a machine T' such that, after T halts, it rewrites the instantaneous description to some otherwise unreachable instantaneous description q_x\,s_0. Therefore, the function we are looking for would be take T, modify it with the usage of M' : [T' \;=; M'(T)] and take q_x ,s_0 as an instantaneous description. Then
[M(T) \;=\;(T',\,q_x\,s_0),]
and by construction (T',q_x\,s_0)\in W if and only if T\in V. This completes the reduction.

Summarizing, the problem of instantaneous descriptions is equivalent to the Input Finiteness problem, since any Turing machine can be viewed as a pair “machine + instantaneous description” and vice versa.

9. Proof that the Input Finiteness problem is undecidable

Let’s assume that we may determine whether a particular Turing machine has finitely many halting inputs or not.

Now let’s prove that such ability leads to the solution of the Halting problem.

Imagine that we have a Turing machine T and input x. We want to determine whether T halts on x or not.

Let’s build a Turing machine T' with the following rules:

T' ignores its own input y.
It simulates T on input x.
If T(x) halts → then T′ halts.
If T(x) does not halt → then T' does not halt.

Let’s notice that if T halts on x, then T' halts on every input, meaning that T' halts on infinitely many inputs, so T' does not belong to V. Otherwise, T' halts on zero inputs, which is finitely many, meaning that T' belongs to V.

Knowing this, we may determine when T halts on x:
If T' does not belong to V, then T halts on x.
If T' belongs to V, then T does not halt on x.

Since we can determine by the finite number of operations whether the Turing machine belongs to V or not (our initial assumption), we can determine by the finite number of operations whether a Turing machine halts on a particular input or not, meaning that the Halting Problem is solvable, which is a contradiction2

Hence, the Input Finiteness Problem is undecidable, which leads to undecidability of all previous problems, including the initial one.

10. Conclusion

During the research we analysed a chain, consisting of 3 problems of set finiteness. Eventually, the chain finished with the Halting problem, allowing us to conclude that all of the problems in it are undecidable, as it was initially assumed.

The knowledge of boundaries of solvability may help developers impose limitations on their requests, so that it will be clear that the program cannot get to an infinite cycle and allow them to be sure that the result will be received eventually. In particular, this research will be useful in topology questions, where it’s necessary to determine properties of a finitely presented fundamental group (in fact, finitely presented semigroup). So understanding that 3 problems are not computable helps to put new fundamental limitations to the applied topology.

This chain may be further used for understanding the decidability of more complicated questions, for instance, whether the determination that the semigroup with the same conditions is computable or not, decidable or undecidable.

It also should be considered that the solution is not optimized. The amount of steps may be reduced. For instance, during the research we found out that the Input Finiteness Problem can be reduced directly to the Halting Problem, while initial research used an auxiliary problem for determining that reduction. So it must not be undermined that there might be a way to reduce the initial problem directly to the Halting problem.

One of the interesting limitations which can be added to the initial list of conditions and make it decidable is a limit on the length of the word in the set. This limitation will impose boundaries on other problems in the chain, making it difficult to repeat the same reasoning and reduce it to the Halting problem.

Hence, this problem may and must be further investigated or used as an auxiliary problem for other problems of the same nature.

References

  1. J. J. Rotman, An Introduction to the Theory of Groups, Springer, pp. 420–430. [↩] [↩] [↩] [↩] [↩] [↩]
  2. A. Marks, Computability Theory, 2024, Accessed on 25 February 2024.
    Covered sections: 2.1–2.2, 3.1, 4.1–4.2, 5.© The National High School Journal of Science 2025NHSJS Reports [↩]

RELATED ARTICLESMORE FROM AUTHOR

LEAVE A REPLY

Please enter your comment!
Please enter your name here