Violent crime remains a significant concern in the United States, but the crime rate is not the same everywhere. Some neighborhoods face much higher levels of violence than others, and identifying the factors that drive these differences is important for both research and policy. This study uses LASSO (Least Absolute Shrinkage and Selection Operator) regression to analyze the Communities and Crime dataset from the University of California, Irvine Machine Learning Repository, which contains census, policing, and crime data from 1,994 U.S. communities. Unlike the past studies, this project removed race-related variables in order to focus on the structural and socioeconomic factors most directly related to crime. The model identified eleven predictors that strongly correlated with violent crime rates, including family-related variables, such as the percentage of children living with two parents and the percentage of children born to never-married parents, as well as housing factors like homelessness, dense housing, and vacant households.
Keywords: Crime, Crime Prediction, Crime Factors, Violent Crime, Data Science, LASSO Regression, Data Analysis.
Introduction
Violent crime remains a significant concern in the United States, shaping public safety, community well-being, and policy debates. While national crime rates have fluctuated over the past several decades, the distribution of violent crime is highly uneven across communities, with some neighborhoods experiencing higher levels of violence than others. Understanding the factors that drive these differences is critical for developing effective prevention strategies and informing public policy.
Violent crime has been linked to factors such as family dynamics, socioeconomic disadvantage, housing instability, and community resources1. Research shows that structural and socioeconomic conditions like poverty, unemployment, family breakdown, and inadequate housing are strongly associated with higher crime rates, as they increase stress, weaken community cohesion, and reduce neighborhoods’ ability to regulate behavior2. Yet many of these factors are deeply interconnected, as poverty is linked to housing instability3, which in turn contributes to family stress, making it difficult for traditional models such as ordinary least squares (OLS) regression to separate their effects. As a result, researchers increasingly turn to modern statistical tools that can better identify the most important predictors while reducing the risk of overfitting. One such method is LASSO (Least Absolute Shrinkage and Selection Operator) regression, which introduces a penalty that shrinks the impact of less important variables toward zero while retaining the more influential ones4. This approach is particularly valuable when analyzing datasets with a large number of noise variables.
Our LASSO regression was applied to the Communities and Crime dataset from the University of California Irvine (UCI) Machine Learning Repository5. The dataset combines information from the 1990 U.S. Census, the 1990 Law Enforcement Management and Administrative Statistics (LEMAS) survey, and the 1995 FBI Uniform Crime Reports (UCR), covering nearly 1,994 U.S. communities and 128 social, economic, and law enforcement variables. There has been previous work done with LASSO regression on this dataset, which included race-related variables6.
The structural inequality framework says that crime is primarily a product of adverse socioeconomic conditions rather than inherent categorical attributes such as racial information7. Race-related variables, such as the percentage of the population that is White or Black, often reflect a range of underlying structural factors, including systemic poverty, unequal access to education, and limited economic opportunities. Including both race and direct measures of these structural and socioeconomic conditions, such as the percentage of vacant housing that is boarded up, in the model would introduce multicollinearity and, more importantly, would risk conflating correlation with causation. To focus on structural and socioeconomic factors, and as the new idea in this study, we removed race-related variables from the dataset, helping the LASSO regression free structural and socioeconomic factors that are most closely associated with violent crime rates.
It is important to acknowledge that real-world crime data may reflect systemic biases. Reporting rates, policing intensity, and enforcement levels can vary across communities and may disproportionately target marginalized populations8. As a result, some variables, particularly those involving race or law enforcement activity, may capture disparities in surveillance or reporting rather than actual differences in criminal behavior (see our discussions for residual dotplot (Fig. 3) and Q-Q plot. (Fig. 4))
By analyzing the predictors retained by the model, we identified eleven predictors that strongly correlated with violent crime rates. These included family-related variables, such as the percentage of children living with two parents and the percentage of children born to never-married parents, as well as housing factors like homelessness, dense housing, and vacant households. This paper offers evidence that can inform both academic understanding and policy debates surrounding violent crime in American communities. We also evaluate the accuracy and discuss the limitations of our current approach. Although our analysis is applied on the data collected in 1990 and 1995, the same method can be applied to similar data and obtain more current results.
Methodology
We will discuss the main analysis strategy in this section. It is designed to identify the most significant structural and socioeconomic factors associated with violent crime rates in communities.
Regression methods
Linear regression provides a natural starting point for this type of analysis, as it models the relationship between a dependent variable (in this case, violent crime rate per 100k population) and a set of independent variables by estimating how changes in the predictors correspond to changes in the outcome. This framework is particularly suitable here because our goal is to understand how community-level characteristics, such as divorce rates and the number of full-time police officers, contribute to variation in violent crime rates, and regression allows both the direction and strength of these associations to be taken into account.
We also notice that ordinary linear regression performs poorly when there are many noise variables, even if the relation is virtually linear. In such cases, the estimates can become unstable and the model may overfit the data, reducing its predictive power on new data. To address this issue, we used LASSO regression, which is a penalized regression method9. LASSO regression helps deal with noise variables that may distract from the most influential variables. The method applies a penalty parameter (lambda), which gradually reduces the size of the coefficients of less important variables. As lambda increases, coefficients for variables with little impact on the model are all squeezed to zero As a result, those variables are mathematically removed from the model. This property makes LASSO regression especially useful for datasets which contain a large number of noise variables. By retaining only the most influential variables, LASSO regression can produce a relatively more accurate model away from overfitting. See Abraham and Lin (2019) for more details of using LASSO regression to produce a predictive model6.
Freeing structural and socioeconomic variables
Research shows that higher crime rates in minority communities are caused by structural disadvantages like poverty and segregation, not by race itself. For example, Ulmer, Harris, and Steffensmeier (2012) demonstrated that disparities in violent crime across White, Black, and Hispanic communities are largely explained by differences in poverty and family structure, not race itself10. Similarly, Peterson and Krivo (2010) argued from a racial-structural perspective that neighborhood crime differences reflect inequalities in resources, segregation, and criminal justice exposure, not inherent traits11. Additionally, ecological studies across multiple U.S. cities found that racial and ethnic concentrations in neighborhoods are linked to higher homicide rates. However, these associations weaken substantially once social disadvantage, such as unemployment and low education, is taken into account12.
Mathematically, when predictors are highly correlated, LASSO may arbitrarily select one over another, potentially excluding equally important variables. Therefore, excluding race-related variables from the analysis helps free the most direct structural and socioeconomic drivers of violent crime rates, avoids reinforcing racial stereotypes, and aligns with well-established sociological and criminological theory. By doing so, we were able to focus on the structural and socioeconomic variables that influence crime rates, rather than racial categories.
Framework of analysis
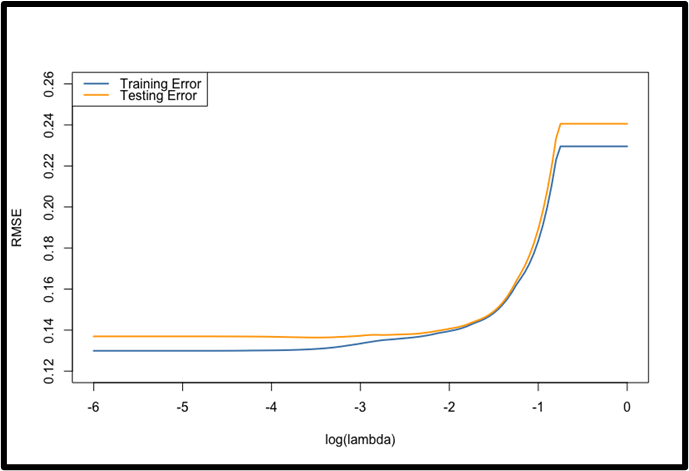
To carry out the analysis, we began by splitting the data into training and testing sets in order to evaluate how well the model performs later. Within the LASSO regression framework, the key tuning parameter is lambda, which controls the strength of the penalty. The penalty is weak when the lambda is small, and the model behaves much like ordinary linear regression, risking overfitting because it retains too many potential noise variables. When lambda increases, the penalty becomes stronger, shrinking nearly all coefficients to zero and producing a model that is too simple, with large prediction errors. We will then choose an optimal model away from overfitting and over-biased.
Based on this property, we plotted a diagram, containing the curves for training error and testing error, over a wide range of lambdas. We then observe the change of training and testing errors, as well as their gaps, and then handpicked a reliable model that had relatively small training and testing errors and small gaps between them. In the reliable model, we will be able to identify the structural and socioeconomic factors that most strongly correlate with violent crime rates.
Data Analysis
Data Cleaning
We filter the dataset as follows:
- The first five columns were removed. They contained identifier string variables, such as community name and state.
- Sixteen variables were removed. They had 30% of entries missing. Note that this approach may introduce bias if the missingness is not random.
- Sixteen race-related variables were removed. These variables included the percentage of the population that is White and the per capita income for Black people in the community.
In total, 37 variables were removed, and 91 variables remained for further analysis.
According to the UCI Machine Learning Repository, all numeric data was normalized into the decimal range 0.00-1.00 using an unsupervised, equal-interval binning method13.
ViolentCrimesPerPop (number of violent crimes per 100k population) was identified as the dependent variable.
Optimal Lambda Selection
The modeling procedure was implemented in R using the glmnet package for LASSO regression. The dataset was split into training (70%) and testing (30%) subsets using random sampling.
We first examined the error curves by plotting the root mean squared error (RMSE) against log(lambda) (see Fig. 1).
As discussed in the Methodology section, Framework of analysis, the optimal log(lambda) lies between -2.50 and -1.50. This range captures the region in which the model achieves low testing error while avoiding overfitting. As lambda increases in the region between -2.50 and -1.50, testing RMSE remains relatively constant for a while, meaning the model is stabilized there. A low error rate, combined with a small gap between the training and testing errors, indicates a well-performing and accurate model.
In order to further determine the optimal value of lambda, a table of log(lambda) values between –2.50 and –1.50 was constructed to inspect the errors against the number of active variables. Here the active variables are defined to be the variables without zero coefficients (see Table 1).
| log(lambda) | Active Variables | RMSE Train | RMSE Test |
| -2.50 | 25 | 0.1360 | 0.1380 |
| -2.45 | 24 | 0.1362 | 0.1380 |
| -2.40 | 23 | 0.1365 | 0.1381 |
| -2.35 | 22 | 0.1367 | 0.1383 |
| -2.30 | 21 | 0.1370 | 0.1385 |
| -2.25 | 20 | 0.1374 | 0.1388 |
| -2.20 | 17 | 0.1378 | 0.1391 |
| -2.15 | 19 | 0.1383 | 0.1395 |
| -2.10 | 16 | 0.1387 | 0.1399 |
| -2.05 | 13 | 0.1391 | 0.1402 |
| -2.00 | 12 | 0.1395 | 0.1407 |
| -1.95 | 12 | 0.1399 | 0.1410 |
| -1.90 | 11 | 0.1404 | 0.1415 |
| -1.85 | 11 | 0.1411 | 0.1420 |
| -1.80 | 11 | 0.1419 | 0.1427 |
| -1.75 | 11 | 0.1428 | 0.1436 |
| -1.70 | 9 | 0.1437 | 0.1444 |
| -1.65 | 7 | 0.1445 | 0.1453 |
| -1.60 | 7 | 0.1455 | 0.1463 |
| -1.55 | 7 | 0.1468 | 0.1476 |
| -1.50 | 6 | 0.1483 | 0.1491 |
Notably, the model stabilizes in both predictive accuracy and variable selection between log(lambda) values of –1.90 and –1.75, with 11 active variables. We selected the optimal log(lambda) as –1.90, which corresponds to a lambda value of 0.01259.
Results
Active Variables
The final model with log(lambda) = –1.90 retained eleven predictors, which represent the community-level characteristics most strongly associated with violent crime rates. The selected variables included family structure, such as percentage of kids born to never married parents, and housing, such as the number of homeless people counted in the streets, and were ranked based on coefficient values. Because the data was normalized, a higher absolute value of a coefficient reflects higher impact, and positive or negative reflects a correlation with increase or decrease in violent crimes, respectively (see Fig. 2).
The active variables were also ranked by the absolute value of their coefficients in order to compare their impacts on violent crime rates. Descriptions were added for the variables (see Table 2).
| Variable Name | Description | Coefficient Value |
| PctKids2Par | Percentage of kids in family housing with two parents | -0.2980 |
| PctIlleg | Percentage of kids born to never married parents | 0.2897 |
| Intercept | Intercept | 0.2887 |
| NumStreet | Number of homeless people counted in the street | 0.1368 |
| PctPersDenseHous | Percent of persons in dense housing | 0.1347 |
| HousVacant | Number of vacant households | 0.1177 |
| MalePctDivorse | Percentage of males who are divorced | 0.0513 |
| TotalPctDiv | Percentage of population who are divorced | 0.0461 |
| PctWorkMom | Percentage of moms of kids under 18 in labor force | -0.0299 |
| PctHouseOccup | Percent of housing occupied | -0.0256 |
| pctUrban | Percentage of people living in areas classified as urban | 0.0141 |
| PctVacantBoarded | Percent of vacant housing that is boarded up | 0.0126 |
Model Performance
RMSE
The model’s root mean squared error (RMSE) is 0.1415. To evaluate the model’s performance, it was compared against a baseline model that used the mean of the target variable as predictions for all observations. While the baseline model has an R-squared of 0, our fitted model achieves an R-squared of 0.6680, indicating that it explains 66.80% of the variance in the data and provides a considerable improvement over the baseline. This is similar to the R-squared of 0.6614 of the LASSO model on the same dataset in previous work6. In that work, the race-related variables are included. This finding supports our assumption that race serves as a reflection of underlying inequalities in structural and socioeconomic factors.
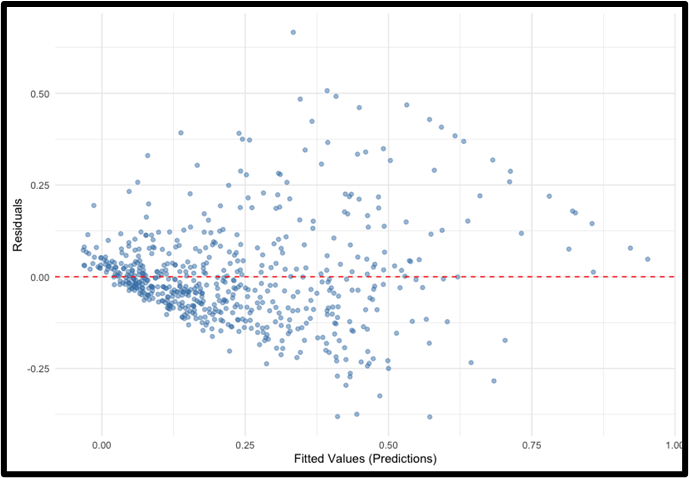
Residual Dotplot
A residual dotplot was created to further understand the fit of the model (see Fig. 3).
The residuals are generally centered around zero, indicating that the model does not over- or under-predict violent crime rates across most communities. However, the spread of residuals increases as fitted values rise, suggesting the presence of heteroscedasticity, or the model’s prediction error grows larger in communities with higher observed crime rates. This pattern indicates that while the LASSO model captures much of the baseline variation in violent crime across communities, it is less precise in accounting for extreme outcomes. The greater spread of residuals at higher predicted values indicates possible unrecorded variables, nonlinear relationships, or structural and socioeconomic differences in high-crime communities that the current model does not fully capture.
Quantile-Quantile Plot
Additional insight into the residuals is provided by a quantile-quantile (Q-Q) plot (see Fig. 4).
The points follow the expected line fairly closely near the center of the distribution but deviate noticeably in the tails, especially at the high end. This pattern indicates heavy-tailed behavior, suggesting the presence of outliers or skewed prediction errors in communities with high crime rates.
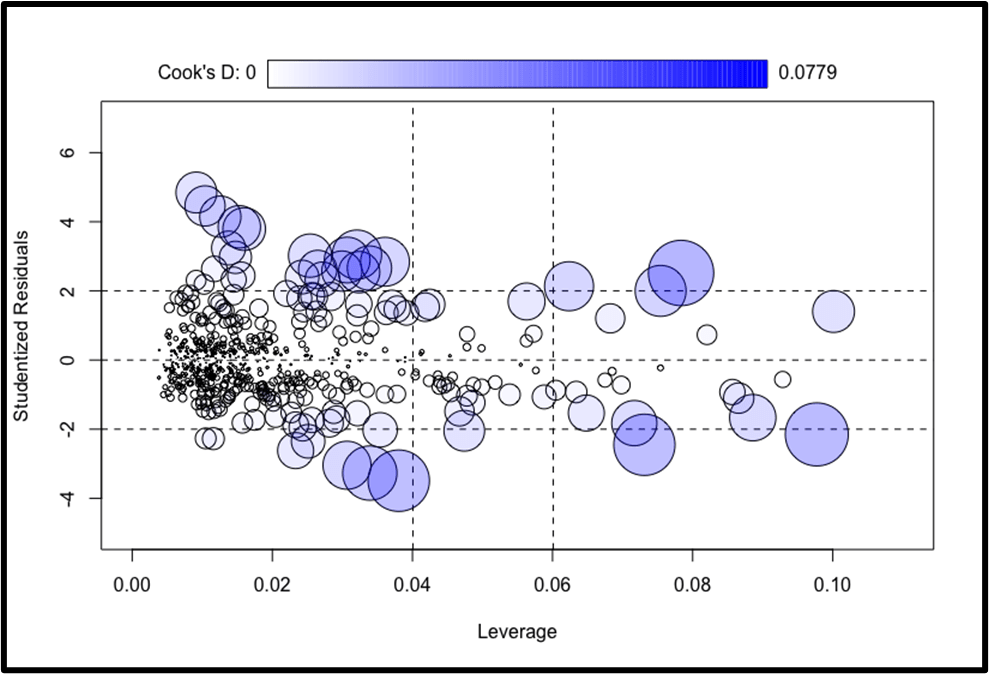
Residual vs. Leverage Plot
Further assessment of model robustness is provided by the residuals versus leverage plot (see Fig. 5).
Most of the observations fall close to the origin of the plot, showing low leverage and small residuals. This means that for most communities, their data does not have an unusually large effect on the overall regression fit. A handful of points appear farther out, with higher leverage or larger residuals, and some of these also have noticeably larger bubble sizes, which reflect higher Cook’s distance. Cook’s distance measures how much influence a single case has on the regression model as a whole. If a case has both high leverage and a large residual, it can pull the regression line in its direction and distort the model’s results. In this plot, while there are a few cases with moderately higher Cook’s distance, none are large enough to dominate the model. This indicates that the model’s results are not being driven by a small number of unusual communities.
Together with the residual dotplot and Q-Q plot, these results show that the model performs well for moderate levels of violent crime but struggles at the extremes, where errors are larger and not normally distributed.
Discussion
The analysis identified key community-level factors associated with violent crime rates, with the final model retaining eleven predictors. Because the race-related variables were removed prior to the application of LASSO regression, we believe these variables reflect more realistic structural factors than those studies including the race variables. Our active variables were plotted on a table, ranked by the absolute value of their coefficients (impacts) from high to low, along with the variables of the other study6 (see Table 3).
| Our Model | Previous Work | ||
| Variable Name | Description | Variable Name | Description |
| PctKids2Par | Percentage of kids in family housing with two parents | PctIlleg | Percentage of kids born to never married parents |
| PctIlleg | Percentage of kids born to never married parents | PctKids2Par | Percentage of kids in family housing with two parents |
| NumStreet | Number of homeless people counted in the street | PctFam2Par | Percentage of families (with kids) that are headed by two parents |
| PctPersDenseHous | Percent of persons in dense housing | racePctWhite | Percentage of population that is caucasian |
| HousVacant | Number of vacant households | PctYoungKids2Par | Percent of kids 4 and under in two parent households |
| MalePctDivorse | Percentage of males who are divorced | – | – |
| TotalPctDiv | Percentage of population who are divorced | – | – |
| PctWorkMom | Percentage of moms of kids under 18 in labor force | – | – |
| PctHouseOccup | Percent of housing occupied | – | – |
| pctUrban | Percentage of people living in areas classified as urban | – | – |
| PctVacantBoarded | Percent of vacant housing that is boarded up | – | – |
The findings of previous work, with race-related variables included, includes less active variables than our model. The four non-race related variables all pertain to family structure, highlighting the impact of family dynamics on crime rates. In particular, when race-related variables are removed, the percentage of the population that is White, more structural and socioeconomic factors appear, such as housing situations and homelessness.
Our findings align with existing literature highlighting the impact of family dynamics and housing instability on community safety. For instance, studies have shown that children in single-parent households face higher risks of victimization and offending, often due to associated socioeconomic challenges14. Similarly, neighborhoods with high levels of homelessness and dense housing are frequently linked to increased crime rates15.
In light of these findings, several policy implications emerge. First, interventions aimed at strengthening family structures, such as programs supporting two-parent households and providing resources for single-parent families, may be beneficial. Second, addressing housing instability through affordable housing initiatives and support for homeless populations may reduce crime rates.
While the model demonstrates reasonable predictive accuracy (R-squared = 0.6680, RMSE = 0.1415), diagnostic checks highlight several limitations. The residual-versus-fitted plot shows that the spread of the residuals increases at higher predicted values, suggesting that the model is less reliable in estimating crime rates for communities with high levels of violence. Similarly, the Q-Q plot reveals deviations in the tails, particularly at the upper end, indicating that the model underestimates crime rates in neighborhoods with the highest levels of violence. While the model provides a good fit, these patterns suggest that it may not fully capture all the underlying complexities in the data. This could be due to subtle nonlinear trends or the influence of variables not included in the model.
The data from Communities and Crime dataset is now several decades old and not every US community is included. As a result, the findings may not fully capture present-day conditions or patterns of crime in all regions of the country. This suggests that future work should apply similar methods to more recent and geographically diverse datasets.
Because of these issues, the policy implications should be interpreted with caution. The results reveal correlations between family structure, housing instability, and violent crime rates, but they do not prove causation. For example, while programs that strengthen family support or provide stable housing for vulnerable populations may help reduce crime rates, this study cannot confirm a direct cause-and-effect relationship. Establishing such links would require more rigorous methods, such as research that tracks communities over time or policy experiments that test the impact of specific interventions in real life.
Conclusion
In this study, we used LASSO regression to identify key structural and socioeconomic factors associated with violent crime rates, highlighting the central roles of family structure and housing instability. The findings demonstrate that higher percentages of children born to never-married parents and greater numbers of homeless individuals are strongly correlated with elevated crime rates. While the model explains a substantial portion of the variance in violent crime rates across communities (R-squared = 0.6680), there are still limitations to this study, particularly in predicting extreme crime rate outcomes, suggesting that the model may not have fully captured the underlying complexities of the data.
These results emphasize that interventions aimed at supporting stable family environments and addressing housing instability may help low violent crime rates, though causal claims cannot be drawn from this analysis alone. Future research should examine additional factors, such as community cohesion, policing practices, and access to social services, and use longitudinal or experimental designs to better understand the potential relationships between these factors and violent crime rates.
Overall, this study contributes to understanding the structural and socioeconomic factors that correlate with violent crime rates and provides evidence to inform both policy discussions and further academic inquiry.
References
- R. J. Sampson & W. J. Wilson. Toward a theory of race and urban inequality. American Sociological Review. 60(6), 265–290 (1995). [↩]
- C. Webster, S. Kingston. Poverty and crime review. Joseph Rowntree Foundation (2014). [↩]
- D. C. McCoy, C. C. Raver. Household instability and self-regulation among poor children. Journal of Child Poverty, 20, 131–152 (2014). [↩]
- R. Tibshirani, Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological). 58, 267–288 (1996) [↩]
- M. Redmond. Communities and crime [dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C53W3X (2009). [↩]
- A. Abraham, K. Lin. Communities and crime: A study on factors related to violent crime rates in the United States. STEM Fellowship Journal (2019). [↩] [↩] [↩] [↩]
- J. M. Timberlake. Great American City: Chicago and the enduring neighborhood effect by Robert J. Sampson. Journal of Urban Affairs, 35(3), 385–392 (2013). [↩]
- D. Buil-Gil, A. Moretti, S. H. Langton. The accuracy of crime statistics: Assessing the impact of police data bias on geographic crime analysis. Journal of Experimental Criminology, 18, 515–541 (2022). [↩]
- IBM. What is lasso regression? https://www.ibm.com/think/topics/lasso-regression (2024). [↩]
- J. T. Ulmer, C. T. Harris, D. Steffensmeier. Racial and ethnic disparities in structural disadvantage and crime: White, Black, and Hispanic comparisons. Social Science Quarterly. 93, 799–819 (2012). [↩]
- L. J. Krivo, R. D. Peterson, D. C. Kuhl. Segregation, racial structure, and neighborhood violent crime. American Journal of Sociology, 114, 1765–1802 (2009). [↩]
- R. Jones-Webb, M. Wall. Neighborhood racial/ethnic concentration, social disadvantage, and homicide risk: An ecological analysis of 10 U.S. cities. Journal of Urban Health. 85, 662–676 (2008). [↩]
- P. A. R. Putri, S. S. Prasetiyowati, Y. Sibaroni. The performance of the equal-width and equal-frequency discretization methods on data features in classification process. Sinkron: Jurnal dan Penelitian Teknik Informatika. 8, 2082–2098 (2023). [↩]
- H. Stritzel, C. S. Gonzalez, S. E. Cavanagh, R. Crosnoe. Family structure and secondary exposure to violence in the context of varying neighborhood risks and resources. Socius. 7, 1–13 (2021). [↩]
- M. C. Lens, I. G. Ellen, K. O’Regan. Neighborhood crime exposure among housing choice voucher households. Assisted Housing Research Cadre Report (2008). [↩]