Abstract
Spinning black holes, or Kerr black holes, house within them a kind of singularity that is quite different from what the common folk imagine them to be. At the heart of Kerr black holes lies a singularity that takes the form of a one-dimensional circular ring of substantial radius and, at the same time, negligible thickness, which brings with it some pretty mind-boggling implications and possibilities. The primary aim of this paper is to provide a comprehensive analysis of the physical and causal properties of the Ringularity (ring singularity) and of the bizarre implications that it comes with. These implications include possible inter-universal travel and travelling back in time using the “Carter Time Machine”, both of which will be explored in the paper. The research dives into the underlying math to theoretically investigate the ring while exploring its physical interpretations through various schematic diagrams. By the end of the paper, the reader should have an in-depth understanding of the ring singularity.
Keywords: Kerr Black Holes, Ringularity, Singularity, inter-universal travel, Carter Time Machine
1. Introduction
The common notion of a black hole is the one in which the black hole is perfectly static and non-rotating. The one in which a tiny point of infinite density is hidden behind a large, terrifying Event Horizon, the boundary that separates the known from the unknown. These black holes are called Schwarzschild Black holes, and they are far from the truth. In reality, there are no perfectly spherical and non-rotating black holes with a point-like singular Core within. The reason being that since all black holes (at least according to our current knowledge) form from the collapse of a dying star, and since all stars spin, it is quite logical to assume that the black hole formed will have no choice but to account for the angular momentum of the star and hence possess some spin too. Hence, along with a huge fraction of the mass of the star, the black hole will also have a characteristic spin associated with it. This assertion is supported by observational findings too since a non-spinning black hole is yet to be discovered. So, there are 2 fundamental properties of black holes to talk of: its mass and its spin (there is also charge, but for convenience, neutrality is assumed), instead of just the mass. Now, the addition of spin as a fundamental property changes things a lot!
For starters, the black hole goes from a uniform sphere to an ellipsoidal, bulging at the equator and flattening at the poles. It also doubles the number of event horizons, as it has 2 of them: the inner and outer horizons. Finally, the dimensionless point sitting at the centre becomes a one-dimensional ring of infinite density. The ringularity is a crucial component of the Kerr Metric, the ultimate solution to Einstein’s Field Equations for uncharged and rotating black holes. The metric sits at the heart of black hole astrophysics as it is one of only 4 metrics that describe space-time near/inside black holes and is the closest among them to describe a real-world black hole (since they are usually uncharged and spinning).
Coming back to the ring, the existence of this ring instead of an “end of space-time” singularity opens up a wild variety of possibilities, some of which will be explored in this paper. However, it is necessary to prove the existence of the ring itself before discussing any of those possibilities. Since this proof can’t be based on observational findings (for obvious reasons), a thorough mathematical proof must suffice. This, will become a frequent occurrence throughout the paper.
2. Mathematical proof of the existence of the ring.1.
2.1 Using Boyer-Lindquist coordinates
the Kerr Metric, in BL(Boyer-Lindquist) coordinates, is given by:
The line element is given by:
![]()
where ![]() and
and ![]() .
.
Also, the Boyer–Lindquist to Cartesian transformation is:
![]()
![]()
![]()
Now, since the core lies at ![]() and
and ![]() :
:
![]()
![]()
A point lying on ![]() and
and ![]() is given by:
is given by: ![]() , which are the parametric coordinates of a circle.
, which are the parametric coordinates of a circle.
2.2 Using Kerr-Schild Coordinates:
![]()
![]()
![]()
![]()
![]()
![]()
Which implies that the geometrical makeup of the interior takes the form of several confocal ellipsoids, each corresponding to a particular r value, as illustrated in the following figure:
Ellipsoidal surfaces in Kerr-Schild frame for different r values when r = constant.2.
Another way to approach the equation is as follows:
Since ![]() ,
, ![]() ,
,
therefore: ![]()
![]()
Dividing by ![]() :
:![]()
Keeping ![]() constant, the above equation describes a hyperboloidal structure as shown.
constant, the above equation describes a hyperboloidal structure as shown.
Half-hyperboloidal surfaces are obtained at θ=constant. The disc at the centre represents the ring singularity3. In both cases, there comes a point where these 3-dimensional structures lose one of their spatial dimensions and become one dimensional circular curves. In both cases, at r=0, the z-axis component vanishes (since ![]() ) and hence only 2 spatial dimensions are left. As a result, a symmetrical ellipse (or a circle) is obtained in the xy plane (represented by the solid line at the centre). To conclude, it can be said that the existence of the ring is quite unavoidable, regardless of the choice of coordinates or constancy.
) and hence only 2 spatial dimensions are left. As a result, a symmetrical ellipse (or a circle) is obtained in the xy plane (represented by the solid line at the centre). To conclude, it can be said that the existence of the ring is quite unavoidable, regardless of the choice of coordinates or constancy.
3. Comparing a traditional singularity with a Ringularity
Now that the mathematical proof of the ring’s existence is dealt with, it’s time to study its properties through a brief comparative analysis of it with a traditional point-singularity. The first and the most obvious difference between them is their geometrical makeup- a singularity is a dimensionless point with no spatial dimensions to define. While the ring is a one-dimensional circular curve with a substantial radius and 0 thickness. Its radius is given by the spin parameter ‘a’, which is equal to the ratio of the black hole’s angular momentum to its mass. i.e. a = J/M. The main differentiating factor however, is the fact that while the ringularity is a physical ring in space, the point singularity doesn’t exactly have a physical existence, instead, it is a moment, a point in time itself. This property of the point is called ‘spacelike’ nature, while the ring is timelike4.
This means that while the ring is a physically approachable celestial body, the point singularity is an inevitable point in the life of an astronaut who has found himself beyond the inescapable event horizon of a non-spinning black hole. To understand why this discrepancy arises, the behaviour of light cones in the vicinity/inside both black holes needs to be analysed:
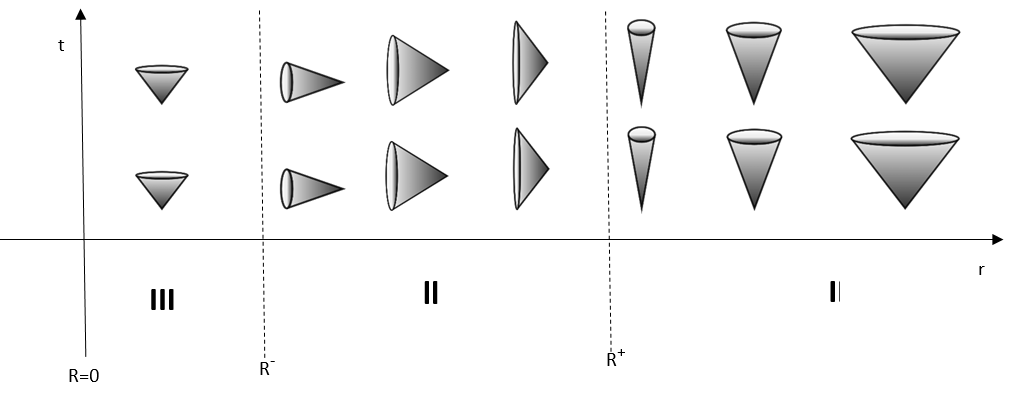
Depiction of light cones in the vicinity of a Schwarzschild Black hole. Here, Rs = Schwarzschild radius, i.e. radius of the event horizon. Block I is analogous to Minkowski(flat) spacetime, while Block II is the interior of the black hole4.
Starting with the simpler, non-rotating case, the light cones in block I behave as normal light cones do, i.e., they point in the time direction. However, upon crossing the event horizon (denoted by Rs), these cones flip in such a way that they now point in the r direction (r = radial distance from the centre of the black hole), with all the cones leading to R = 0. This means that R = 0, i.e., the singularity has become an unavoidable point in time that anything crossing the horizon will eventually reach. The reason for this “flipping” of cones is that for values of r < Rs, the coefficient of dR² and that of dt² switch signs, signifying the fact that space and time “switch roles” beyond Rs. Thus, as one moves forward through time on Earth, if one finds oneself inside a black hole, the inevitable progression through different values of r occurs before finally reaching annihilation at R = 04.
Light cones near and inside a Kerr black hole. Their behaviour resembles that of those near a non-rotating black hole up until block II, after which the discrepancy arises, the light cones flip back to their initial orientation upon crossing the inner horizon (R–), resulting in a timelike ringularity at R=04. On the other hand, if one observes the behaviour of light cones near/inside a Kerr black hole, it can be deduced that although the initial flipping does occur at R+ (outer horizon), this flipping is cancelled out by an equal and opposite flipping which occurs at R- (inner horizon). Therefore, beyond the inner horizon, the light cones point ‘up’ in the direction of time, and hence space and time are reverted to their initial roles. This implies that the inner ergosphere is a region that can be explored physically, just like any other place in space-time. It should be noted however that this seemingly flawless flipping of time cones is only possible in the most ideal conditions, with no matter to cause any perturbations. The gravity of the hole is kept at bay by the anti-gravitational effect of the spinning black hole. A couple of Penrose diagrams will now be used to help visualize this stark difference between the two singularities.
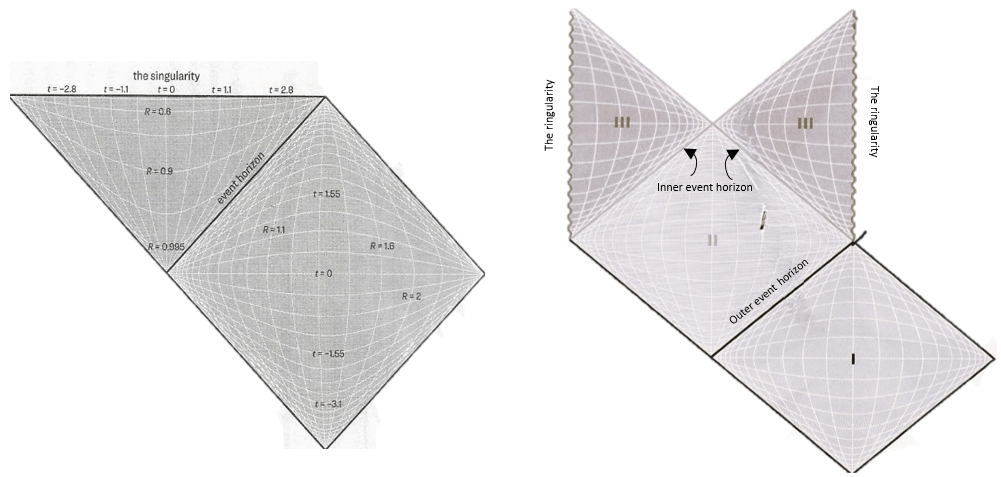
Penrose diagrams of Schwarzschild and Kerr Black Hole spacetime. The vertical curved lines represent the singular space coordinate while the horizontal ones represent the time coordinate5.
Here, the vertical-ish lines represent the singular space coordinate (for simplicity, only one of 3 dimensions is taken) while the horizontal ones represent the time coordinate. Again, if the non-spinning case is taken first, it can be seen that upon crossing the event horizon, space and time switch places. This means that inside the black hole, the horizontal lines represent the space coordinate. The singularity is not a point in space, but instead is represented by a horizontal line in the Penrose diagram, implying that it is a point in time that must be hit if one plunges into the black hole. Now, shifting attention back to the Kerr Black hole, the ring is represented by two vertical lines (corresponding to the two sides from which the ring can be approached). This means that the ring is, in fact, a physically occurring entity, unlike its non-rotating dimensionless counterpart. While the singularity is an unavoidable point in time that everything and everyone has to reach once crossing the horizon, the ringularity is a physical body that can be very much avoided. This apparent avoidability of the ring has some pretty interesting implications, which will be explored soon enough.
4. The Pseudo-Singular Nature of the Ring
This section can be considered as a continuation of the previous one, as the primary aim here is to highlight the apparent “pseudo-singular” nature of the ring singularity and show how it is quite different from the traditional “end of space-time” singularities found at the centre of Schwarzschild black holes. To do so, let’s understand what is meant by the “singular” nature of the point singularity. In 1965, Roger Penrose published the Penrose Singularity Theorem, in which he provided a comprehensive proof of the fact that point singularities are inevitable consequences of gravitational collapse at the end of the lifespan of a sufficiently massive star, and that these points are singular, i.e. they are regions where null geodesics terminate. He basically proved that all geodesics that cross the event horizon are incomplete in finite affine length, which proves the existence of a singular point (a point where geodesics are incomplete) beyond the horizon. The main crux of his proof was the existence of FALLs (Finite Affine Length Light) beyond the event horizon, which, according to him, implied an inevitable singularity inside the black hole.
The issue here is that while this logic stands for Schwarzschild black holes (black holes that aren’t even real!), it doesn’t hold for Kerr ones (the ones that do exist). In the Kerr case, geodesics with a finite affine length don’t always end up at the ringularity6, thereby defying the apparent inevitability of the singularity and showing that all trajectories that cross the event horizon(s) do not have to face imminent annihilation at the hands of a singularity. To provide substance to this assertion, the focus will be on 2 families of null geodesics, the “fast” ones and the “slow” ones that, despite having a finite affine length, do not terminate at the ring singularity.
They are given by the general equations:
![]()
![]()
or,
![]()
4.1 The Slow ones(k+):
The “slow” ones are given by:
The “slow” ones are given by:
![]()
The roots of this quadratic give the radii of the inner and outer horizons. So, when ![]() , which means the velocity of the light ray at those radial distances is also 0. Due to this, an outgoing/slow light ray can never penetrate either of the horizons because its velocity tends to 0 as it approaches them. Hence it can be deduced that these geodesics are asymptotic to both the horizons as
, which means the velocity of the light ray at those radial distances is also 0. Due to this, an outgoing/slow light ray can never penetrate either of the horizons because its velocity tends to 0 as it approaches them. Hence it can be deduced that these geodesics are asymptotic to both the horizons as ![]() and
and ![]() , meaning they never cross them. Now, since r is an affine parameter for this ray, the affine length of it comes out to be
, meaning they never cross them. Now, since r is an affine parameter for this ray, the affine length of it comes out to be ![]() ) , which is obviously a finite quantity, making it a FALL. It is interesting to note despite having a finite affine length, this geodesic does not terminate at a singularity, contrary to Penrose’s assumption.
) , which is obviously a finite quantity, making it a FALL. It is interesting to note despite having a finite affine length, this geodesic does not terminate at a singularity, contrary to Penrose’s assumption.
4.2 The Fast ones:
What about the slightly “faster” ones? For simplicity, the choice will be the one with the least complications and the one that is easiest to track: The Axial one, an incoming axial light ray falling head-on into the black hole from either of the poles. This ray faces no problem whatsoever in its journey as it penetrates straight through both R+ and R–. Now, since nothing is compelling it to end up at the ring, this ray goes through the ring and emerges out the other side as a slow geodesic (strictly theoretically speaking, and well, also according to the math). One might argue that the ray being talked about here doesn’t have a finite affine value and hence can’t be considered in this discussion, but to the cynic’s dismay, the geodesic can be parameterized to show that it is in fact a FALL, by proving that the integral of its affine parameter is finite. The parameterisation can be found in the appendices. The fact that there are 2 FALLs that do NOT terminate at a singularity shows how the ring is not a traditional singularity that gobbles up all the geodesics that fall inside the black hole7 This indicates that the ring is quite “pseudo-singular” by nature. The singularities that exist in real life might not be as terrifying as often imagined. The question that might arise next is where this fast FALL ends up. Mathematically speaking, there is no reason to doubt that it does in fact go straight through the “throat” of the black hole and reach the “other side,” but where does it go? What lies on this “other side” and, more importantly, is this other side reachable?
5. Venturing beyond the Ring singularity
It is time to take the plunge and explore what might lie beyond the Ringularity. Contrary to common lines of thought, the focus will NOT be on the Maximal extensions of Kerr spacetime, since these mainly emphasise paths that avoid the ring altogether or those that go around it. Instead, an unconventional (but mathematically sound) approach will be used to predict what might lie beyond the ring.
To begin, let’s view the Kerr metric again, but in Kerr-Schild coordinates(t,x,y,z):
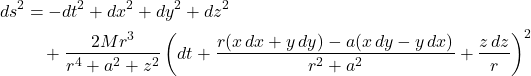
Which mainly depends on a function r (x,y,z) given by:
![]()
Now, not counting the 2 complex solutions, the given biquadratic will have 2 solutions: a positive and a negative one8. An engineer or an experimental physicist might be tempted to discard the latter as a “fake” or non-physical solution. But for a theoretical physicist? But for a theoretical physicist, such things aren’t thrown out that easily. As long as something is mathematically valid, it is kept—because sometimes, the universe hides its best secrets in the places that don’t make immediate sense. Another reason for considering r values <0 is that if r is only restricted to positive values, for a timelike geodesic, the derivative of its tangent vector ![]() becomes discontinuous. This problem is fixed if r is allowed to assume negative values as well. This newfound freedom bifurcates the Kerr space-time into 2 regions: one for r>0 and the other for
becomes discontinuous. This problem is fixed if r is allowed to assume negative values as well. This newfound freedom bifurcates the Kerr space-time into 2 regions: one for r>0 and the other for ![]() , separated by the ring at r=0. The spacetime identified by
, separated by the ring at r=0. The spacetime identified by ![]() is asymptotically flat and lacks any horizons9. The following figure helps in visualising a manifold formed by patching the 2 space-times together. The top of r>0 side of the disc is identified with the bottom of the
is asymptotically flat and lacks any horizons9. The following figure helps in visualising a manifold formed by patching the 2 space-times together. The top of r>0 side of the disc is identified with the bottom of the ![]() side, and vice versa.
side, and vice versa.
The 2 manifolds on either side of the r=0 ring. The region denoted by r>0 represents our universe, while the latter represents the one on the other side. The thick arrows are the trajectories of astronauts brave enough to venture beyond the ring. So, a person entering the ring from the r>0 side will emerge from the top side of the r<0 space-time10.
Now here’s the interesting part: this new universe that has just been discovered through plain math isn’t just a carbon copy of the existing universe. In this region, gravity pushes instead of pulls, producing a sort of anti-gravitational repulsion that counteracts the gravity of the original universe. Crossing the ring and emerging on the other side means encountering no horizons, but instead being expelled into space with tremendous force11 ,12. This force is unofficially termed as “anti-gravity” and the universe harbouring it an “anti-verse.” The root cause of such anomalous behaviour can be derived from the underlying math. As always, math opens doors that don’t appear to exist! In the Kerr metric, the term ) governs the gravitational potential of an object in the vicinity of a Kerr black hole13. Now it’s clear that if r becomes negative, so does the term, which implies the effective gravitational potential (Veff) of an object on the other side also becomes negative. The negative sign, according to the standard sign conventions of physics, indicates repulsion, which causes the in falling objects to accelerate away from the ring on the other side instead of toward it. This force also causes the incoming geodesics to curve away from the ring on the other side, which produces a sort of apparent repulsion effect. This “anti-gravity” is not to be confused with a similar theorized effect produced as a result of the existence of a positive cosmological constant (such as dark energy), and instead is a result of the geometry of the Kerr Black holes, which cause the effective gravitational potential to flip signs for r<0.
It should be noted, however, that this possibility is purely the result of blindly following the math, without any correlation to the observational findings of the real thing. When dealing with realistic situations, however, the infalling matter creates a substantial hindrance by causing what’s known as “mass inflation” instability: a bizarre phenomenon in which the infalling matter experiences relative infinite blueshift near the inner horizon (since particles gain infinite energy upon approaching it). The incoming and outgoing streams (here, outgoing streams refer to the backscattered waves which get reflected outward) collide with such immense energy that they create a feedback loop: the process in which the accelerated interactions of the mass particles cause the effective mass parameter (Meff) inside to increase exponentially. This ultimately leads to the destruction of the inner horizon and the creation of a spacelike singularity,
While it does seem as though a brick wall has been hit, there is a way to solve this problem, too, even though that way is as impractical as it gets. If, somehow, some “negative mass” is introduced into the mix, it could, in theory, disrupt the pile up of energy near the horizon by repelling some of the mass away and hence prevent the consequent feedback loop from growing too rapidly and greatly. Additionally, it would suppress the energy growth of Meff by introducing negative energy density into the mix and hence prevent the spacelike singularity.
6. Naked singularities and possible to-and-fro traversability
In the previous section, the bizarre possibility of an ‘anti-verse’ looming beyond the ringularity was discussed. Now the sad part is that even if such universes do exist, they are forever locked behind the dual event horizons of black holes, which means that although it’s theoretically possible to get to the other side of the ring, coming back to our universe isn’t exactly an option, or is it? The answer to this question for a Schwarzschild black hole is a stone-cold “no”; it isn’t. But those fictional, non-existent black holes aren’t the focus here. When considering real-world black holes (the ones that spin), a wild possibility arises.
To explore this possibility, a term called the Radius of the innermost stable circular orbit or ![]() , is defined, which is the least distance from which one can have a stable circular orbit around a body. For Kerr black holes, this value is dependent on the spin parameter:
, is defined, which is the least distance from which one can have a stable circular orbit around a body. For Kerr black holes, this value is dependent on the spin parameter: ![]() or
or ![]()
![]() orbits, the greater the value of a, the smaller the
orbits, the greater the value of a, the smaller the ![]() value. The reason is that the tremendous angular momentum of the black hole produces a sort of anti-gravitational effect that opposes the gravity of the black hole, allowing objects to orbit in stable circles closer than if it weren’t spinning. So basically, as the a value (ratio between the angular momentum and mass of the black hole) increases, the
value. The reason is that the tremendous angular momentum of the black hole produces a sort of anti-gravitational effect that opposes the gravity of the black hole, allowing objects to orbit in stable circles closer than if it weren’t spinning. So basically, as the a value (ratio between the angular momentum and mass of the black hole) increases, the ![]() value shrinks. But how far can it shrink? If it shrinks and becomes equal to or less than the radius of the outer event horizon, it would cause the horizon to disappear altogether, making to-and-fro travel into the black hole a real possibility. But is it possible to reduce
value shrinks. But how far can it shrink? If it shrinks and becomes equal to or less than the radius of the outer event horizon, it would cause the horizon to disappear altogether, making to-and-fro travel into the black hole a real possibility. But is it possible to reduce ![]() to that extent? To answer this question, there’s a need for a connecting variable that relates the radius of the event horizon with that of the innermost stable orbit, and the spin parameter perfectly meets that requirement:
to that extent? To answer this question, there’s a need for a connecting variable that relates the radius of the event horizon with that of the innermost stable orbit, and the spin parameter perfectly meets that requirement:
For Kerr black holes, the radius of the outer event horizon is given by:
![]()
Clearly, for ![]() ,
, ![]() or
or ![]() . Computing
. Computing ![]() for
for ![]() shows that it also shrinks down to the same value14. The calculation demonstrating this can be found in the appendices section. If the value of
shows that it also shrinks down to the same value14. The calculation demonstrating this can be found in the appendices section. If the value of ![]() is increased beyond unity,
is increased beyond unity, ![]() implying that there are stable circular orbits even beyond the event horizon. This would cause the horizon to disappear since it is no longer the boundary of no return. The disappearance of the event horizon would leave the ringularity “Naked” and quite accessible to the rest of the universe, with the potential for returning.
implying that there are stable circular orbits even beyond the event horizon. This would cause the horizon to disappear since it is no longer the boundary of no return. The disappearance of the event horizon would leave the ringularity “Naked” and quite accessible to the rest of the universe, with the potential for returning.
Now, it is a well-known fact that the cosmic censorship conjecture does not allow such exposed singularities to exist, since the theory clearly suggests that all singularities must be hidden/locked behind an event horizon in order to preserve the deterministic nature of the universe. Despite this, the possibility of an exposed ringularity is considered because the monstrous singularity capable of violating the deterministic nature of the universe is not the one located at the core of Kerr black holes. Instead, a pseudo-singular one exists (as discussed earlier), which doesn’t represent the end of space-time and hence doesn’t defy the laws of physics as known.
So, the implication is that if the value of a is somehow tipped above 1, even by a small fraction then theoretically, it would be possible to go through the ring while also having the option to return. This opens up prospects of utilizing the ringularity as a doorway for inter-universal travel. The question now, is that how can it be done? How can the seemingly universal threshold limit set for the spin parameter be exceeded, be it through natural occurrence or through artificial interference? Or in other words, how to increase the value of a beyond unity?
According to the existing research in the field, the largest possible value of a for near-extremal black holes is given by ![]() , a result that could be observationally verified by LISA (Laser interferometer space antenna for gravitational wave measurements), a space based gravitational wave detector expected to be launched in 203515. Now, while this is the generally accepted limit for naturally occurring black holes, it is theoretically possible to exceed this limit artificially. It is possible to “overspin” the black hole by adding objects which possess a substantial angular momentum in the same direction as that of the black hole. These objects should preferably oblate spheroids, which are geometrically similar to the physical structure of spinning black holes16 The number of such objects needed depends upon how close the initial value of a is to reaching 1.
, a result that could be observationally verified by LISA (Laser interferometer space antenna for gravitational wave measurements), a space based gravitational wave detector expected to be launched in 203515. Now, while this is the generally accepted limit for naturally occurring black holes, it is theoretically possible to exceed this limit artificially. It is possible to “overspin” the black hole by adding objects which possess a substantial angular momentum in the same direction as that of the black hole. These objects should preferably oblate spheroids, which are geometrically similar to the physical structure of spinning black holes16 The number of such objects needed depends upon how close the initial value of a is to reaching 1.
7. The Carter Time Machine
It must be said that some pretty bizarre properties and implications of the ring have been discussed so far, but the one about to be discussed might just top the list. Having already plunged through the ring and explored the uncharted area ahead, it’s time to take a step back and talk about the region that is bounded by the ringularity., the region where it is theoretically possible to explore all those time paradoxes that have been meddling with the minds of physicists and physics enthusiasts alike for quite some time. This region, where it is possible to travel backwards in time, has our ring as its equator and is denoted by ![]() . Now, the reason for such sci-fi like property lies in the sign of the Kerr metric component:
. Now, the reason for such sci-fi like property lies in the sign of the Kerr metric component: ![]() , which determines the behaviour of the azimuthal angle φ, and is given by:
, which determines the behaviour of the azimuthal angle φ, and is given by:
![]()
now for values of r>0, this component stays positive and therefore spacelike[ ]. However, since r assumes negative values in the region ξ, for sufficiently large values of ![]() , the entire component
, the entire component ![]() becomes negative and hence timelike. Meaning, as the azimuthal angle changes for an object, it can travel through time in a timelike curved path (called CTCs: Closed Timelike Curves) and return to the same spot in space (and time!) from which it began.
becomes negative and hence timelike. Meaning, as the azimuthal angle changes for an object, it can travel through time in a timelike curved path (called CTCs: Closed Timelike Curves) and return to the same spot in space (and time!) from which it began.
7.1 Construction of a CTC17.
A comprehensive mathematical derivation of a CTC is given below:
Let’s take any 2 points: ![]() ; now our goal is to prove that there exists a future as well as a past pointing timelike curve from p to q.
; now our goal is to prove that there exists a future as well as a past pointing timelike curve from p to q.
Let ![]() ; and
; and ![]()
Let the future pointing and past pointing curves α and β be the future and past pointing timelike curves from p to q.![]() is defined as:
is defined as:
![]()
Where ![]() is an arbitrarily large constant and
is an arbitrarily large constant and ![]() is the space-time interval (
is the space-time interval (![]() ). Also,
). Also, ![]() and
and ![]() . Now, in order to know about the behaviour of the curve as it progresses, it is differentiated with respect to
. Now, in order to know about the behaviour of the curve as it progresses, it is differentiated with respect to ![]() to obtain its tangent vector:
to obtain its tangent vector: ![]() . Now this vector is timelike if and only if its dot product with itself, i.e.
. Now this vector is timelike if and only if its dot product with itself, i.e. ![]() is negative, this condition can be satisfied by setting a large enough value of
is negative, this condition can be satisfied by setting a large enough value of ![]() , which only signifies the rate at which the azimuthal angle changes (
, which only signifies the rate at which the azimuthal angle changes (![]() ).
).
Similarly, a past pointing curve ![]() can be defined as:
can be defined as:
![]()
Here, the terms ![]() and
and ![]() determine how the azimuthal angle and the time coordinate of the curve change. For a large constant B, the curve remains future pointed in the sense of the region’s timelike vector field while the time coordinate steadily decreases, implying a past-pointing curve. Equipped with 2 disjointed curves that have the same endpoints but differ in their causal direction, there is now a need for a timelike curve that will take one back in time and also act as a “bridging curve” connecting
determine how the azimuthal angle and the time coordinate of the curve change. For a large constant B, the curve remains future pointed in the sense of the region’s timelike vector field while the time coordinate steadily decreases, implying a past-pointing curve. Equipped with 2 disjointed curves that have the same endpoints but differ in their causal direction, there is now a need for a timelike curve that will take one back in time and also act as a “bridging curve” connecting ![]() and
and ![]() , thereby completing a fully functional CTC. This bridging curve is given by:
, thereby completing a fully functional CTC. This bridging curve is given by:
![]() Where
Where ![]() ,
, ![]() , and
, and ![]() is sufficiently smaller than 0.
is sufficiently smaller than 0.
Now, its tangent vector is:![]()
To check the timelike nature, the dot product with itself must be negative:![]()
![]()
![]() }
}
Now, since ![]() , the term
, the term ![]() will dominate over the other terms for large values of B, making the dot product negative, and hence it can be said that the curve is timelike.
will dominate over the other terms for large values of B, making the dot product negative, and hence it can be said that the curve is timelike.
It can also be proven from further analysis that it is a future-pointing curve. A fully functional time machine (CTC) can now be constructed from the curves taken:
![]()
7.2 Working of a CTC: Travelling through its segments
Let us now use our very own time machine (CTC) to travel back in time!
- First, follow curve
 to go from point
to go from point 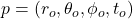 to
to 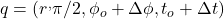 where
where  is sufficiently negative.
is sufficiently negative.
2. From point , follow the curve
, follow the curve  that will take you backwards in time while keeping your spatial coordinates constant (here, only
that will take you backwards in time while keeping your spatial coordinates constant (here, only  and
and  are spatial). The amount of time gone backwards can be determined by letting
are spatial). The amount of time gone backwards can be determined by letting  run as long as desired.
run as long as desired.
3. Say the curve brings you to time
brings you to time  and azimuthal angle
and azimuthal angle 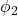 . Now, to return to the starting position, follow the curve
. Now, to return to the starting position, follow the curve  . You are now at the same position you began from but at a time much before yours.
. You are now at the same position you began from but at a time much before yours.
Now, while the existence of CTCs is mathematically sound, it is purely based on classical mechanics. When the quantum effects are also considered into the picture, their usage as potential time machines seems far from feasible. According to the Quantum field theory, no region in space-time is really empty, even spaces with complete vacuum are fille with invisible quantum fields which fluctuate millions of times per second, giving rise to virtual particles which get instantly annihilated after being formed. However, when these particles are formed in the vicinity of the inner horizon, they are infinitely blue shifted by the extreme curvature, which provides them enough energy to turn into real particles. This creates an infinite flux of particles, which prevents the CTCs from ever being formed. This is the main crux behind the chronology protection conjecture18) according to which the quantum mechanical laws of the universe prevent causality from being violated, thereby preventing CTCs as well.
Nonetheless, the prospect of man somehow managing to counteract the quantum effects in the distant future in order to access time travel is an exciting one to say the least.
8. Future Research Directions
In the last few sections, the discussion focused on how the ringularity could theoretically serve as a medium to a) venture into another universe and b) travel back in time, whilst also outlining the practical impossibility of both based on current technological capabilities. Mitigating the discrepancy between theory and practicality appears to be well out of reach, but a couple of ground-breaking discoveries and inventions could do the trick, so let’s talk about them individually.
In section 6, the possibility of a naked singularity was examined, illustrating that in order to expose the ringularity to the rest of the universe, there is a need to increase the ratio of the angular momentum of the black hole to its mass beyond unity, which is the focus moving forward. The process is surprisingly simple in logic, though obviously not in practice (not yet, at least). The idea is to throw in objects with the same direction of spin as the black hole, which would cause their angular momentum to simply add up to that of the black hole. The main hurdle lies at the point when a = 1. Since naturally occurring black holes can’t have the value of ‘a’ greater than 1, uncertainty remains regarding whether it is possible to artificially push its value beyond 1, which is essential for progress. Although the nearest black hole is quite far (about 10,000 light years away), once reached, exposing the ring should be the next move to venture beyond it and explore the “antiverse” that lies beyond.
The other concept to pursue is even more far-fetched than trying to spin a black hole so fast that its event horizon disappears: Negative mass. As discussed in section 5, to survive a trip to the centre of the black hole long enough to use the Carter time machine or travel to the other side, it will be necessary to address the perturbations caused by the presence of mass in that region. This, in theory, can be achieved by introducing some negative mass into the equation. The challenge is that negative mass does not currently exist, so that must be addressed. The invention or discovery of this type of exotic matter would represent a significant step toward the exploration of black holes. Theoretically, placing a sufficiently large negative-mass shell near the ringularity could counteract the effects of normal mass in the vicinity, potentially preventing the theorized infinite blue shifting of any infalling normal matter and thus averting the creation of a spacelike singularity.
9. Conclusion
The following section serves as a summary to conclude the entire paper. The paper began by proving how the ring singularity is an inevitable consequence of the geometry of spinning black holes, regardless of the coordinate system used or perspective. The ellipsoidal and hyperboloidal structures formed by holding r and theta constant respectively, lost one of their spatial dimensions at r=0 and transformed into a one-dimensional ring. The properties of the ring were examined by comparing it with a traditional singularity, noting how one is spacelike while the other is timelike, implying that while a point singularity represents a moment in time, the ring is a physically occurring celestial body.
In section 4, the pseudo-singular nature of the ring was discovered, suggesting it doesn’t consume all the geodesics that cross the horizons and that navigation around or through the ring is indeed possible. This apparent avoidability of the singularity opened up the possibility of exploring what lies beyond the ring, as discussed in section 5, albeit from a purely theoretical standpoint. The prospect of an ‘antiverse’ was also considered, arising from a value of r less than 0.
Now, The existence of an entire universe beyond the ring holds no meaning unless there is a means of exploring it, while also having the option of returning. Although returning to our universe isn’t feasible for naturally occurring black holes, decreasing the radius of the innermost stable circular orbit around a black hole to below that of the outer event horizon makes two-way travel a viable option. This can theoretically be accomplished by tipping the value of the spin parameter over unity, even by a tiny fraction. Doing so would result in a ‘naked singularity’ that is accessible, allowing for a return to the universe. In a nutshell, the potential of utilising the ring as a medium for inter-universal travel was explored.
In the last and concluding section, the prospect of travelling backwards in time by using the unconventional geometry of the area bounded by the ring was examined. The timelike nature of the azimuthal angle for r values less than 0 indicated that an object would travel back in time as its azimuthal coordinate continued to change inside the region denoted by . In conclusion, the exploration of ring singularities within Kerr black holes reveals a profound shift in the understanding of black hole structure and behaviour. By dissecting the mathematical framework and physical implications of the ringularity, it is highlighted how it sharply contrasts with traditional singularities. This opens avenues for theoretical advancements, including concepts like closed timelike curves and potential traversability.
As the complexities of these spinning giants continue to be grappled with, the research presented lays the groundwork for future investigations into the nature of black holes and their wild properties. That said, this research is merely a culmination of the work done by those who came before. The aim of the paper was to take the existing information and present it in a brief but comprehensive manner, and the author feels that the objective has been achieved.
10. Methodology
The entire research was carried out independently by the author over the course of 5 months: from December 2024 to April 2025, which included gathering all the available information/knowledge on the subject, finalising the topics and concepts to be included, structuring the paper in a way that is coherent and smooth, and formulating the very drafts. Extensive reading on the topic was done prior to this period to gain conceptual understanding as well as the mathematical aptitude required to take on this task. The apparatus used included the author’s laptop, his phone, along with various books like “The Geometry of Kerr Black Holes” by Barrett O’ Neill, “Black Holes” by Brian Cox and Jeff Forshaw, etc. The majority of the information, however, was obtained from IPs available online, including a recently published paper by R.P. Kerr himself, titled “Do Black Holes have singularities?”; notes on the Kerr metric and gravitation by the Department of Physics, University of Rome “La Sapienza”, among others. All the sources mentioned, along with a few others, have been referenced in the bibliography section. The mathematical analysis was conducted using tensor calculus and geodesic equations in Kerr spacetime. The Kerr metric was studied in multiple coordinate systems (e.g., Boyer–Lindquist and Kerr–Schild coordinates), and its implications were analysed in the context of Penrose–Carter diagrams and causal structures.
11. Appendices
1. Parameterization of the fast geodesic
Let us first write down the radial equation of the incoming geodesic. Since the angular momentum and the polar angle are null, the equation simplifies to:
![]()
![]()
Integrating both sides:
![]()
Which gives:![]()
Now, taking ![]() and
and ![]() :
:
![]()
Now, at ![]() , clearly
, clearly ![]()
i.e. the affine parameter ![]() remains finite as well as smooth at
remains finite as well as smooth at ![]() , no blow-up, no divergence. Hence proved, the ingoing axial geodesic is in fact a FALL, at least on our side of the ring
, no blow-up, no divergence. Hence proved, the ingoing axial geodesic is in fact a FALL, at least on our side of the ring ![]() .
.
2. Relation between RISCO and the spin parameter a14
The Kerr ISCO formula is given by:
![]()
Where
![]()
![]()
And ![]()
Putting ![]()
![]()
![]()
So,![]()
Which gives:![]()
Hence proved, for ![]() ,
, ![]()
References
- D. Bini, A. Geralico. The Kerr spacetime: Rotating black holes in general relativity. Department of Physics, University of Rome “La Sapienza”. https://www.roma1.infn.it/teongrav/onde19_20/kerr.pdf (2019). [↩]
- D. Bini, A. Geralico. The Kerr spacetime: Rotating black holes in general relativity. Department of Physics, University of Rome “La Sapienza”. https://www.roma1.infn.it/teongrav/onde19_20/kerr.pdf (2019). [↩]
- D. Bini, A. Geralico. The Kerr spacetime: Rotating black holes in general relativity. Department of Physics, University of Rome “La Sapienza”. https://www.roma1.infn.it/teongrav/onde19_20/kerr.pdf (2019). [↩]
- B. Cox, J. Forshaw. Black holes. London: William Collins (2022). [↩] [↩] [↩] [↩]
- B. Cox, J. Forshaw. Black holes. London: William Collins (2022). [↩]
- R. P. Kerr. Do black holes have singularities? arXiv. https://arxiv.org/abs/2312.00841 (2023) [↩]
- R. P. Kerr. Do black holes have singularities? arXiv. https://arxiv.org/abs/2312.00841 (2023). [↩]
- C. W. Misner, K. S. Thorne, J. A. Wheeler. Gravitation. San Francisco: W. H. Freeman and Company (1973 [↩]
- G. Montani. Addendum 4: Kerr metric and rotating black holes. Sapienza University of Rome. [↩]
- G. Montani. Addendum 4: Kerr metric and rotating black holes. Sapienza University of Rome. https://www.roma1.infn.it/teongrav/onde19_20/addendum4.pdf (2020). [↩]
- C. W. Misner, K. S. Thorne, J. A. Wheeler. Gravitation. San Francisco: W. H. Freeman and Company (1973 [↩]
- B. Carter. Global structure of the Kerr family of gravitational fields. Physical Review Journal: https://doi.org/10.1103/PhysRev.174.1559 (1968). [↩]
- S. Chandrasekhar. The mathematical theory of black holes. Oxford: Oxford University Press (1983). [↩]
- L. C. Stein. Kerr ISCO calculator. https://duetosymmetry.com/tool/kerr-isco-calculator/(2015). [↩] [↩]
- O. Burker, J.R. Gair, J. Simon, M.C. Edwards. Constraining the spin parameter of near-extremal black holes using LISA. Physical Review Journals. https://doi.org/10.1103/PhysRevD.102.124054 (2020). [↩]
- T. Jacobson, T.P. Soutiriou. Erratum. Overspinning black holes with a test body. Physical Review Journals. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.103.209903 (2009). [↩]
- B. O’Neill. The geometry of Kerr black holes. New York: Dover Publications (1995). [↩]
- S.W. Hawking. Chronology Protection Conjecture, Physical Review D.(1992 [↩]