Assessing the Properties of Silicon Anodes for Applications in Sodium-Ion Batteries

Abstract

Sodium-ion batteries are being researched as a low-cost and sustainable alternative to lithium-ion batteries. However, as cell design is being developed, there are questions about efficient electrode and electrolyte materials. Currently, carbon-based compounds are the leading anode material, but silicon’s high specific capacity makes it efficient and its abundance in the crust makes it economically and environmentally ideal. This study employed atomistic simulations to research the use of crystalline (c-Si) and amorphous (a-Si) silicon as sodium-ion battery anode material. Using the Atomic Simulation Environment, c-Si was modeled as a diamond lattice (216 atoms), and a-Si was generated via a melt-quench process (heated to 2300 K and cooled to 300 K). Molecular Dynamics simulations were performed at 300 K with a 1fs timestep to simulate sodium insertion and removal over 25 cycles, assessing structural stability and volumetric changes. Specific capacity was estimated by adding sodium ions until structural instability occurred, and conductivity was estimated using Density Functional Tight Binding (DFTB). Amorphous silicon showed twice the conductivity of c-Si (3.16e-4 S/m), while c-Si achieved a higher average capacity (944.29 mAh/g) and structural stability. After 25 simulated sodium insertion/removal cycles, c-Si retained approximately 80% of its initial volume, indicating partial but significant irreversible shrinkage while a-Si completely deformed. These findings suggest that c-Si can be a potential sodium-ion battery anode material if created into a composite with other materials such as carbon to improve its conductivity and stability.

Keywords: Sodium Ion, Molecular Dynamics, Crystalline Silicon, Amorphous Silicon, Charge Cycle, Specific Capacity, Conductivity

Introduction

Lithium-ion batteries lead the energy storage industry and their flexibility of use lends to their many different applications such as in EVs, grid-connected storage, and electronic devices^1,2,3. They have a high rotund-trip efficiency between 85 and 95% and a suitable balance of power density and energy density^1,4. They also have long life-cycles and are lightweight and safe^5,6. But as demand grows, sodium-ion batteries are a sustainable alternative due to sodium’s higher abundance in the earth’s crust and lower cost compared to lithium.

Similar to a lithium-ion battery, the main components of a sodium-ion battery are a cathode, anode, and electrolyte. As cell design is being developed, material choice is crucial for improving efficiency. The leading class of materials for sodium-ion battery anodes are carbon-based compounds^7,8. Materials such as hard carbon are widely studied due excellent capacity, cycling stability and conductivity^9,10. However, hard carbon has a lower specific capacity of about 300-400 mAh/g compared to other high-capacity materials such as silicon which can have specific capacities of up to 954 mAh/g in sodium-ion systems^9,11. It is important to note that this value is idealized as practical capacities are typically much lower due to weak Na-Si alloying behavior¹².

While hard carbon remains the most widely studied anode for sodium-ion batteries due to its reasonable capacity and cycling stability, it suffers from low initial Coulombic efficiency, a sloped and poorly defined voltage plateau, and limited rate performance, restricting its practical application in fast-charging or high-energy-density systems^13,14. On the other hand, silicon offers a potentially higher capacity and more tunable structure, but it also has its own problems in sodium-ion systems. Poor Na insertion kinetics due to the ion’s larger size, can restrict diffusion through the silicon matrix greatly decreasing efficiency^15,16. Additionally, severe volume changes during sodiation lead to mechanical instability, pulverization, and degradation^17,18. These issues make it difficult to characterize silicon performance through experiments alone. Atomistic simulations can fill this gap by modeling volume deformation, sodium-ion accommodation, and electronic behavior, providing insights often inaccessible through physical testing¹⁹.

I researched the use of crystalline and amorphous silicon as anode material in sodium-ion batteries. To accomplish this, I used Molecular Dynamics and DFTB to measure volume changes over charge cycles and estimate specific capacity and conductivity. Unlike previous studies, this work compares the performances of both silicon materials to each other as well as to other materials being used. My findings contribute to the broader effort of identifying and optimizing silicon-based anodes as well as informing future experimental and modeling work in sodium-ion battery development.

Methods

Crystalline silicon was modeled as a cubic structure with a diamond lattice (Figure 1). A lattice constant of 5.43 Å for silicon was used, consistent with reported values^20,21. The cell dimensions were set to 16.29 × 16.29 × 16.29 Å, and the crystalline silicon had 216 atoms. Periodic boundary conditions were applied in all three dimensions. To create the amorphous silicon, the crystalline structure was gradually heated to 2300 K till it melted. Then the structure was cooled back to 300 K fast enough such that the silicon structure solidified before it could reform into a crystal causing it to develop irregularities^22,23. To remove excessive clumping around the center, the cell size was rescaled to 14.66 × 14.66 × 14.66 Å (Figure 1). The amorphous silicon also had 216 atoms and periodic boundary conditions applied in all dimensions.

Molecular Dynamics was then run to simulate the charge cycles of a battery using the Atomic Simulation Environment (ASE 3.24.0)²⁵. Sodium ions were repeatedly introduced and removed from the surface of the silicon structures and simulated their interactions. In this context, one charge cycle was defined as the insertion of 4 sodium ions onto the silicon surface, equilibration for 10 ps, removal of the 4 sodium ions followed, and another 10 ps equilibration. Each cycle was a total of 20 ps with 1 fs timesteps. The sodium ions were initially evenly spaced and onto one face of the silicon structure. In the simulation, the ions were free to migrate, allowing evaluation of the intercalation mechanisms. After each cycle, the occupied volume of each of the structures was estimated using Monte Carlo sampling. Each of the sample atoms were checked if they fell within the cut-off distance (set to 2 Å) from any of the other atoms. The cell volume was then multiplied by the fraction of atoms inside to estimate the volume. Molecular Dynamics was also used to find specific capacities. To estimate this value, increasing amounts of sodium ions were added to the silicon structures. The maximum amount of sodium ions the structures could hold while maintaining stability was found and then used in the theoretical specific capacity formula.

To run Molecular Dynamics, Langevin and Velocity Verlet, ASE libraries, were used. Langevin is stable and specializes in running accurate simulations at varying temperatures. Velocity Verlet was chosen because of its stability during long simulations. In setting up the environment for the simulation, the Maxwell-Boltzmann distribution was needed as it describes initial velocities of particles based on a given temperature. The Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) was used to set up my Molecular Dynamics calculator²⁶. The Stillinger-Weber potential modeled covalent bonding in the Si-Si interactions by combining two-body and three-body interaction terms. It takes into account that bond energy is related to both bond distance and bond angles. For the Si-Na and Na-Na interactions, the Lennard-Jones potential was used. The potential calculates the forces using the distances between the particles. At the core, close-by particles repel, medium distance particles attract, and particles further and further away stop interacting. The potential also takes into account two key parameters: epsilon (ε) and sigma (σ). ε is the depth of the potential energy well and σ is the distance at which the potential energy between two particles is zero. For the Na-Si interaction ε was 0.255 eV and σ was 2.92 Å.

The final property tested for was the conductivities. Using Density Functional Tight Binding (DFTB+) and Slater Koster Files for silicon, self-sufficient charge calculation (SCC) were performed^27,28. The Fermi level was extracted from the DFTB+ output, and the density of states (DOS) near the Fermi level was analyzed to approximate carrier concentration. In this work, electrons were assumed to be the dominant charge carriers. Carrier concentration was estimated from the DOS value at the Fermi level scaled by an intrinsic factor for silicon, 1.5e16 m^-3, and a constant electron mobility of 0.14 m²/V·s was used. The Drude formula was then applied to calculate conductivity. This approach provides a simplified estimate for relative comparison between structures rather than an absolute prediction as it fails to account for interband transitions, carrier localization, or temperature dependent scattering effects.

For more details regarding the example algorithms and visualization techniques employed, see the code in the data availability section.

Results

Stability

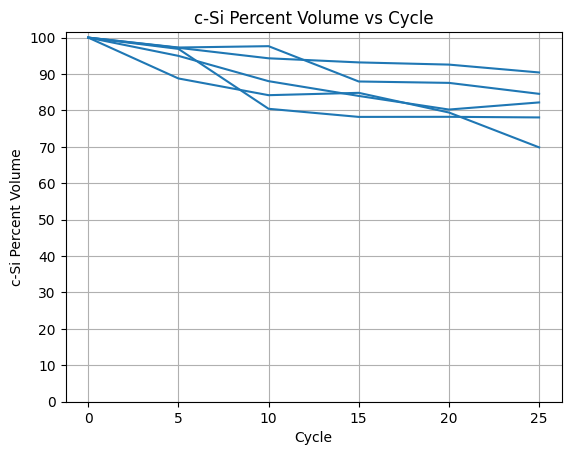
I began my analysis by finding the volume changes that occur during charge cycles. I repeatedly added and removed sodium ions from the silicon surface a total of 25 times in order to simulate 25 different charge cycles. In between each cycle I used the volume function to estimate and save the volume data. For the crystalline silicon, the volume dropped to just above 80% on average with the poorest performance going down to 70% and best up at 90%. For the amorphous silicon, the volume dropped to between 30-40% each time, signifying complete deformation (Figure 2). Atomistic snapshots revealed that crystalline silicon maintained a degree of lattice order and occasionally exhibited local rearrangement that partially restored its structure after sodium removal (Figure 3). On the other hand, amorphous silicon showed no signs of restoration, resulting in much more rapid degradation. Additionally, during the Molecular Dynamics simulations, sodium ions remained primarily adsorbed on the surface of the silicon structures, with minimal penetration beyond the surface layer.

Specific capacity

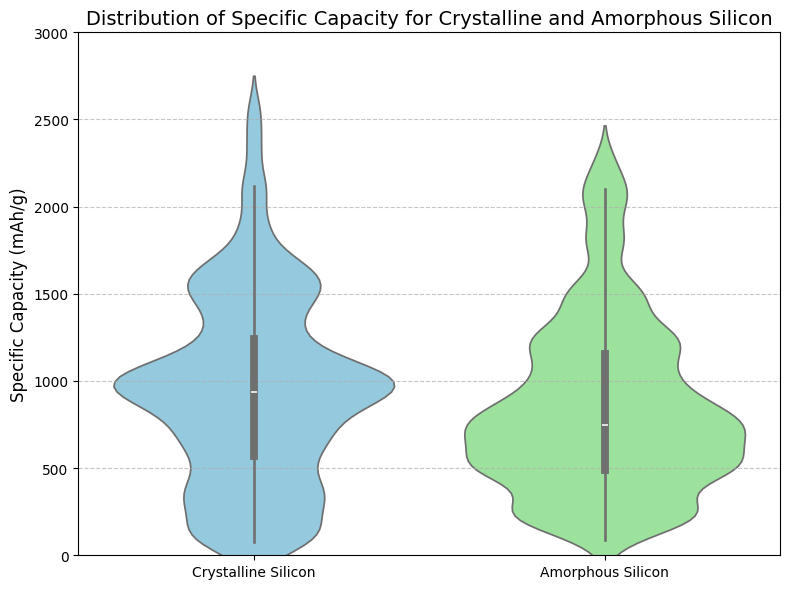
The specific capacity of the silicon structures was also calculated using a Molecular Dynamics simulation. Sodium ions were added in groups of 18 until structural instability occurred. A sodium ion was considered held if it was within 2.5 Å of any silicon atom. For each material, 100 simulations trials were performed to capture variability. Crystalline silicon exhibited an average specific capacity of 944.29 ± 541.04 mAh/g, while amorphous silicon showed 847.82 ± 499.48 mAh/g (Figure 4).

Conductivity

I next used DFTB to calculate the initial conductivities of the structure. To do this I ran a SCC with the Slater Koster files for silicon and used the Drude model to estimate the conductivity. Because the simulations were deterministic the same results were achieved each trial. I found a conductivity of 1.68e-4 S/m for crystalline silicon, and twice that at 3.16e-4 S/m for amorphous silicon.

Discussion

The findings from my simulations offer insights about the use of crystalline and amorphous silicon as anode material in sodium-ion batteries. To better understand these results, it is important to consider the structural factors underlying the observed trends. The superior volume retention of crystalline silicon can be attributed to its ordered lattice, which provides uniform sodium insertion sites and maintains a connected network during repeated cycles. The structure of crystalline silicon allows it to accommodate sodium while limiting irreversible bond breaking, resulting in more gradual volume reduction. In contrast, amorphous silicon lacks order, leading to uneven stress distribution and localized structural collapse upon repeated sodiation and desodiation. Similarly, the higher specific capacity of crystalline silicon compared to amorphous silicon suggests that structural regularity facilitates greater sodium accommodation before instability occurs, whereas the disordered nature of amorphous silicon accelerates structural degradation, reducing its capacity. But, before drawing broader conclusions about silicon in real-world sodium-ion battery applications, several limitations in the simulation setup must be acknowledged.

The major limitation lies in the version of the Lennard-Jones potential I employed. While effective for capturing certain electrostatic interactions, it overlooks the charge of the sodium ion. In reality, sodium ions are positively charged, which would lead to stronger interactions with the silicon surface, which could also carry a charge. Ignoring these charge-based interactions in the simulation likely impacted the stability and the movement of the sodium ions. Without considering the sodium ion’s charge, the model simplified the real forces acting in the system. Incorporating more accurate electrostatic potentials or using more advanced methods such as Density Functional Theory (DFT) in future studies would provide a more realistic and accurate representation of the interactions between sodium ions and the silicon surface.

The second limitation of my simulations was that it did not fully factor in all elements of a realistic environment. I modeled the silicon and sodium ions without taking into account other key parts of a battery. For example, I did not model an electrolyte, leaving out interactions between the nanoparticle and electrolyte and the sodium ion and electrolyte which would influence the interactions between the nanoparticle and the sodium ion. Additionally, the simulation assumed that the sodium ions were introduced on a single surface, enabling controlled assessment of structural changes but not fully capturing realistic sodiation behavior.

The third limitation concerns the Drude model, which was used to calculate the conductivity of the silicon materials. The Drude model mainly considers the movement of free electrons over interband transitions. The latter being more relevant in semiconductors such as silicon. Therefore, the reported values should be interpreted as relative comparisons rather than absolute performance metrics.

Conclusions

I researched the use of crystalline and amorphous silicon in sodium-ion batteries to test if they were suitable anode material. I tested for three criteria: stability, specific capacity, and conductivity. It was found that the crystalline silicon was more stable with its volume dropping to between 70-90% after 25 charge cycles. On the other hand, amorphous silicon completely deteriorated with its volume dropping to between 30-40%. While crystalline silicon was more stable, it is important to note that only 25 cycles were simulated because in real life applications batteries are expected to run hundreds to even thousands of cycles without significant volume changes. Optimized silicon anodes in lithium-ion systems typically achieve structural retention of 80–85% after 100–200 cycles with surface modification strategies^30,31. On the other hand, graphite anodes in lithium-ion batteries lose only 2-5% volume after 500-1000 cycles and hard carbon anodes in sodium-ion batteries lose only 5-7% volume after 500 cycles^32,33. Moreover, the sodium ions remained mainly on the surface with minimal penetration, aligning with known kinetic limitations for sodium ion diffusion in crystalline and amorphous silicon^34,35.

To further understand the properties of crystalline and amorphous silicon, simulations were run to calculate specific capacities and conductivities. Crystalline silicon had an average specific capacity of 944.29 mAh/g and conductivity of 1.68e-4 S/m. Amorphous silicon had an average specific capacity of 847.82 mAh/g and conductivity of 3.16e-4 S/m. The specific capacities are similar to reported values in sodium-ion systems (954 mAh/g), but much lower than those found in lithium-ion systems (up to 4000 mAh/g)^11,36.  While the conductivities were poor, silicon showed promise due to its high specific capacity (for hard carbon anodes it is only 300-400 mAh/g). In future work we would like to experiment with various methods to increase the stability and conductivity of silicon anodes. Ideas include testing silicon-carbon composites and p-type silicon.

The implications of this study are significant, especially as sodium-ion batteries emerge as an alternative to lithium-ion batteries. With sodium’s natural abundance and favorable chemical properties, advances in this field could lead to more sustainable energy storage solutions. This research serves as a first look into the use of silicon anodes in enhancing sodium-ion battery performance.

Data and Code Availability Statement

The code used to generate this data may be found at:

https://colab.research.google.com/drive/13wUtOb7Mr00jFM50-RhRCmN75jrd8_E3

Acknowledgments

I thank Ken Conner for his insights and support.

References

1. M. Martí-Florences, A. Cecilia, R. Costa-Castelló, Modelling and estimation in lithium-ion batteries: A literature review. Energies. 16, 6846 (2023). [↩] [↩]
2. B. Scrosati, J. Hassoun, Y. K. Sun, Lithium-ion batteries. A look into the future. Energy Environ. Sci. 4, 3287–3295 (2011). [↩]
3. A. Masias, J. Marcicki, W. A. Paxton, Opportunities and challenges of lithium ion batteries in automotive applications. ACS Energy Lett. 6, 621–630 (2021). [↩]
4. J. M. Tarascon, M. Armand, Issues and challenges facing rechargeable lithium batteries. Nature. 414, 359–367 (2001). [↩]
5. G. E. Blomgren, The development and future of lithium ion batteries. J. Electrochem. Soc. 164, A5019–A5025 (2017). [↩]
6. T. Horiba, Lithium-ion battery systems. Proc. IEEE. 102, 939–950 (2014). [↩]
7. J. F. Peters, M. Baumann, B. Zimmermann, J. Braun, M. Weil, The environmental impact of Li-ion batteries and the role of key parameters – A review. Renew. Sustain. Energy Rev. 67, 491–506 (2017). [↩]
8. H. Hou, Carbon anode materials for advanced sodium‐ion batteries. Adv. Energy Mater. 7, 1602898 (2017). [↩]
9. C. Wu, Y. Yang, Y. Zhang, H. Xu, X. He, X. Wu, S. Chou, Hard carbon for sodium-ion batteries: progress, strategies and future perspective. Chem. Sci. 15, 6244–6268 (2024). [↩] [↩]
10. Y. Zhao, Y. Liu, H. Zhang, X. Wang, L. Zhang, Y. Zhang, J. Li, H. Liu, A high-performance sodium-ion battery enhanced by macadamia-shell-derived hard carbon anode. Nano Energy. 45, 1–9 (2018). [↩]
11. F. K. Tareq, S. Rudra, Enhancing the performance of silicon-based anode materials for alkali metal (Li, Na, K) ion battery: A review on advanced strategies. Mater. Today Commun. 39, 108653 (2024). [↩] [↩]
12. M. N. Obrovac, V. L. Chevrier, Alloy negative electrodes for Li-ion batteries. Chem. Rev. 114, 11444–11502 (2014). [↩]
13. J. Qian, X. Wu, Y. Cao, X. Ai, H. Yang, High capacity Na-storage and superior cyclability of nanocomposite Sb/C anode for Na-ion batteries. Nano Lett. 15, 3193–3199 (2015). [↩]
14. J. Qian, Y. Cao, Y. Ai, X. Ai, H. Yang, Amorphous phosphorus/nitrogen-doped graphene paper as flexible free-standing anode for high-performance lithium and sodium ion batteries. ACS Appl. Mater. Interfaces. 6, 21562–21566 (2014). [↩]
15. J. Qian, Y. Li, J. Qi, Y. Cai, Y. Tian, X. Ai, H. Yang, High capacity and rate capability of amorphous phosphorus for sodium ion batteries. J. Phys. Chem. C. 119, 10206–10212 (2015). [↩]
16. Y. Wang, S. M. Bak, B. Shadike, X. Yu, Z. Hu, Y. Liu, X. Q. Yang, L. Gu, H. Li, X. Huang, G. Li, Insights into the capacity degradation mechanism of Ni-rich cathode materials by combined operando X-ray diffraction and three-dimensional tomography. Adv. Energy Mater. 8, 1702582 (2018). [↩]
17. S. Li, X. Li, J. Zhang, J. Luo, Y. Wu, Y. Li, Y. Zhang, H. Yu, Silicon/void/graphene yolk–shell nanocomposite as a lithium-ion battery anode with long cycle life. Small. 16, 1905260 (2020). [↩]
18. H. Jia, B. Liu, J. Chen, Z. Li, Y. Liu, G. Zhang, X. Sun, B. Liu, H. Zhang, G. Cao, Rational design of high-performance Li-ion battery anodes from silicon-based bulk metallic glass. Adv. Energy Mater. 10, 2000974 (2020). [↩]
19. M. Li, S. Chen, L. Xu, Y. Li, Y. Liu, Z. Peng, T. Liu, R. Wang, C. Yang, X. Zhang, Ultrathin 2D amorphous Fe–Co–P nanosheets with rich vacancy defects for efficient water splitting. Nano Energy. 96, 107000 (2022). [↩]
20. T. Hom, W. Kiszenik, B. Post, Accurate lattice constants from multiple reflection measurements. II. Lattice constants of germanium, silicon, and diamond. J. Appl. Crystallogr. 8, 459–464 (1975). [↩]
21. P. Becker, P. Scyfried, H. Siegert, The lattice parameter of highly pure silicon single crystals. Z. Phys. B Condens. Matter 48, 17–21 (1982). [↩]
22. R. Yazami, G. Gallezot, P. Roussel, A. Hamwi, Electrical conductivity and intercalation mechanism of some carbonaceous materials with lithium. J. Nucl. Mater. 406, 193–200 (2010). [↩]
23. B. Jache, P. Adelhelm, Use of graphite as a highly reversible electrode with superior cycle life for sodium-ion batteries by making use of co-intercalation phenomena. J. Phys. Chem. C. 118, 28226–28234 (2014). [↩]
24. N. Rego, D. R. Koes, 3Dmol.js: molecular visualization with WebGL. Bioinformatics 31, 1322–1324 (2015). [↩]
25. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng, K. W. Jacobsen, The Atomic Simulation Environment—A Python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017). [↩]
26. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995). [↩]
27. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. Jakowski, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, G. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W. Z. Yu, T. Frauenheim, DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 152, 124101 (2020). [↩]
28. A. Sieck, Structure and physical properties of silicon clusters and of vacancy clusters in bulk silicon. Dissertation, University of Paderborn (2000). [↩]
29. J. D. Hunter, Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 9, 90–95 (2007). [↩]
30. S. Sharma, H. Thakur, A. Saxena, K. R. Basu, P. Sharma, Recent advancements in silicon-based anodes for sodium-ion batteries: A review. Electrochim. Acta 493, 142824 (2025). [↩]
31. L. K. Singh, D. Kumar, S. Prakash, Progress and prospects of silicon-based anodes for sodium-ion batteries. Trans. Indian Inst. Met. 78, 1273–1285 (2025). [↩]
32. J. P. Pender, G. Jha, D. H. Youn, J. M. Ziegler, I. Andoni, E. J. Choi, A. Heller, B. S. Dunn, P. S. Weiss, R. M. Penner, C. B. Mullins. Electrode degradation in lithium-ion batteries. ACS Nano 14, 1243–1295 (2020). [↩]
33. S. Tan, H. Yang, Z. Zhang, X. Xu, Y. Xu, J. Zhou, X. Zhou, Z. Pan, X. Rao, Y. Gu, Z. Wang, Y. Wu, X. Liu, Y. Zhang. The progress of hard carbon as an anode material in sodium-ion batteries. Molecules 28, 3134 (2023). [↩]
34. Y. Xu, Y. Zhu, Y. Liu, C. Wang, Electrochemical performance of porous carbon/tin composite anodes for sodium-ion and lithium-ion batteries. J. Phys. Chem. C 119, 20347–20353 (2015). [↩]
35. M. Ge, J. Rong, X. Fang, C. Zhou, Porous doped silicon nanowires for lithium ion battery anode with long cycle life. Adv. Energy Mater. 2, 1150–1156 (2012). [↩]
36. J. Wang, Y. Zhang, X. Li, Y. Liu, H. Zhang, X. Wang. A brief overview of silicon nanoparticles as anode material: A review. Small 19, 2307275 (2023). [↩]