The Standard Model and Neutrino Oscillation

By
Aleksandra Klovach
-
0
131
Read the Full Article as PDFDownload

Abstract

This paper is a summary of current knowledge on aspects of Standard Model (SM) and Neutrino Oscillation problem. It was written due to the lack of materials that thoroughly explain the subject of Neutrino Oscillation and can give new learners an easy entry into it, without overloading them with scientific jargon and complex math. This paper is a literature review. Methods of this paper is summarizing relevant recent or foundational publications on the topic from credible publishers. This paper provides explanations of relevant to Neutrino Oscillation parts of SM, quantum numbers, basics of  Higgs Mechanism, the concept behind the classical most well-known seesaw theory and details (including basic math) on three seesaw models, an alternative of the Lorentz violation theory, including detailed report on three main models, side to side comparison of seesaw and lorentz violation, and basic overview of experiments on the subject. It gives future physicists an early entry point into a rather complicated subject of Neutrino Oscillation. Hopefully, this will lead to more attention and research on Neutrino oscillations and new discoveries that will further humanity’s understanding of physics.

Keywords: Physics, Particle Physics, Standard Model, Neutrino Oscillation, Seesaw Model, Lorentz Violation, Higgs Mechanism, Quantum Numbers, Neutrinoless Double-beta decay

1. Introduction

The standard model of particle physics is a theoretical framework that summarizes humanity’s understanding of the foundations of the universe.

The standard model is also a predictive framework, that have been consistently experimentally validated. SM has its problems and limitations. One of the most well-known is Dark Matter problem and it has tons of publications explaining it on all levels possible. However, other less-known problems such as Neutrino Oscillation tend to have only highly academic papers that concentrate on one particular subject of it.

This paper’s main goal is to give reader a basic understanding of the Standard Model and its limitations with an accent on the Neutrino Oscillation, including not only classical seesaw models but also less widely-known Lorentz violation theories. This paper is intended to be an easy entry in neutrino oscillations that I lacked while learning it myself. This paper will provide future generations of physicists who only starting their journey with easier entry into the subject, leading to more people concentrating their future studies on it.

The Standard Model is a very detailed picture of particle interactions, but it has its problems which are to be studied and solved.

In Section 3, I provide a breakdown of what we know about the standard model. Section 4 outlines the limitations of it. Section 5 explains the basics of three seesaw models. Section 6 explains the Lorentz violation theory and presents some frameworks it created. Section 8 presents important experiments and findings in the neutrino oscillation problem, but only breathily due to main focus of this paper being theoretical part of the subject.

2.  Methods

This paper presents a literature review of the current understanding of the Neutrino Oscillation problem. The primary goal was to synthesize insights from existing peer-reviewed research to outline theoretical models, experimental results, and ongoing questions in the field.

Sources were selected based on three key criteria:

  • Credibility of the publisher or journal — All articles were drawn from peer-reviewed journals indexed in databases such as Scopus.
    • Relevance to core topics — Priority was given to papers that directly addressed mechanisms of neutrino oscillation, experimental results (e.g., from Super-Kamiokande or DUNE), or theoretical frameworks such as the PMNS matrix.
    • Recency and foundational value — While some foundational papers from earlier decades were included for context, the majority of sources were published within the last 10–15 years to ensure relevance to the current state of the field.

The synthesis process involved grouping research into major themes (theoretical frameworks, experimental evidence, and implications for physics beyond the Standard Model), then summarizing and comparing key findings within each theme. While this paper is not exhaustive, it aims to reflect the most widely accepted models and active debates in the literature as of this writing.

3. The Standard Model

The Standard Model (SM) is the theory that lays in the base of modern particle physics. It describes three fundamental forces (electromagnetic, weak and strong forces, but does not cover gravity) and categorizes seventeen named particles1. The particles are divided into two families: fermions and bosons (see Figure 4).

3.1 Bosons

Bosons are particles that function as force carriers. They have integer spins and can easily occupy the same space at the same time2. Bosons are categorized as gauge and scalar bosons.

  • Gauge Bosons: Particles in this category have spins of 1 and 2 and act as force carriers of one of three fundamental forces: photons for electromagnetic force, W and Z bosons for weak force, and eight types of gluons for strong force)3.
  • Scalar Bosons: Particles in this category have a zero spin and currently only include the recently discovered Higgs boson3. This boson is responsible for the Higgs mechanism, which gives Dirac particles their mass (see Section 3.5 for more details).

3.2 Quantum Numbers

The term quantum number is used in physics and chemistry. It represents a way to quickly define and categorize the behaviors and characteristics of particles within an atom or other quantum system4. Quantum numbers arise from the mathematical solution to the Schrodinger equation. They are labels for eigenvalues associated with conserved quantities (charge, angular momentum, energy). In particle physics, quantum numbers represent how particles transform under internal symmetry groups, providing a group-theoretic origin tied to gauge invariance5.

The most traditional quantum numbers are principal, angular momentum, magnetic, and spin quantum numbers; however, some systems require additional quantum numbers to describe the possible states of it in more detail4.

Subatomic particles require additional colour and flavour quantum numbers6. It is important to understand that these numbers have nothing to do with the colour or flavours we are used to; it is only a way to indicate some states of particles in one word instead of complicated mathematical models.

Flavours are possessed by quarks and leptons, six flavours for each group (up and down, charm and strange, etc. all of them are illustrated on the first three figs).

Colours are possessed by quarks and gluons, it determines how they interact with the strong force. There are three colours – red, green, blue – and three anti-colours – anti-red, anti-green, anti-blue (all colours are illustrated on the first three figs).

3.3 Fermions

Fermions are particles that combine into matter, have spin in odd half-integers, and obey the exclusion principle (they cannot occupy the same space at the same time)2. Fermions are divided into two groups: leptons and quarks. It is important to note that not only fundamental particles (leptons and quarks) are considered to be fermions but also things made of them such as protons, atoms, molecules, and physical objects2. All fermions are divided into three generations1:

  • First Generation: The first generation is the lightest and most stable. It consists of two quarks, up and down quarks, and two leptons, electron, and electron neutrino1.
    Second Generation: The second generation is heavier and less stable; particles of this generation are not able to form stable matter. It consists of charm and strange quarks, and muon and muon neutrino leptons1.
    • Third Generation: The third generation is the heaviest and the least stable (also not able to form stable matter). It consists of top and bottom (also known as beauty) quarks, and tau and tau neutrino leptons1.

Fermions possess colour and flavour quantum numbers (see Figure 2).

Quarks and leptons (see Figure 3).

Figure 3: Illustration of quarks and leptons (including 12 flavours and 6 colours). Image from (5)

The main difference between two groups is that quarks are affected by all four funda- mental forces and have colour quantum numbers, while leptons are subject to all four forces except the strong one and do not possess colour numbers1.

3.4   Lepton Conservation Law

Lepton conservation is a rule in physics that provides a ‘balancing’ effect in particle inter- actions and is usually used to predict results of them6. While quarks possess colour quantum numbers, leptons have lepton numbers. There are three kinds: the electron-lepton number, the muon-lepton number, and the tau-lepton number6.

Each lepton number has a value of +1, -1, or 06. For example, the electron-lepton number +1 value means that a particle is an electron or electron neutrino, -1 – their antiparticle, and 0 none of previously mentioned particles. For muon and tau-lepton numbers math works the same way.

The lepton conservation law states that in any interaction, separate sums of all three numbers must be conserved6. This behavior guarantees the conservation of the total number of positron and electron particles in the universe6. For example, when a neutron decays into a proton, it will emit an electron and an electron neutrino to keep the balance of total lepton number.

3.5  Dirac Particles

In the SM, all fermions are thought to be Dirac particles with half-integer spin properties (i.e., electron with 1/2-spin state)3. Dirac particles get their mass through the Higgs mechanism3, described in more detail in Section 3.6. 

3.6  The Higgs Mechanism

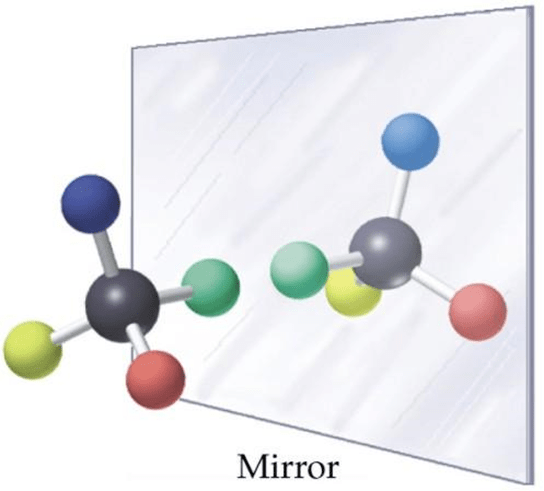
For the Higgs mechanism to occur, a particle must be able to interact with the Higgs field, which requires a chirality condition3. The term chirality means that something exists in two states, which are completely identical to each other except being mirror reflections of each other, making it impossible to superimpose them7.

You may have met this term in organic chemistry, where it is illustrated in Figure 4.

Dirac particles are also chiral, which means that there are right and left-handed versions of them, depending on the direction of their spin relative to their motion. For a Dirac particle to interact with the Higgs field, two chiralities need to transform differently under the electroweak gauge group8.

4. Limitations of the Standard Model

The Standard Model has a number of limitations and exhibited phenomena it cannot de- scribe. These are five of the most famous ones.

4.1   Dark Matter

While studying the movement of galaxies, scientists noticed that actual movement should not be possible with masses and mass centers of these galaxies9. Particle physicists and cosmologists came to the conclusion that there must be an excess amount of  ‘dark’ matter which does not interact with light, to account for the additional mass required to explain the high rotational velocities of objects at large distances from the centers of galaxies9. Currently, the scientific community from astrophysical telescopes to particle colliders and cryogenic experiments are studying dark matter to understand its fundamental properties and how it might fit into the SM.

4.2  Gravity

The SM can explain our fundamental forces as particles that are force carriers. These have been detected for 3 of the 4 forces except gravity. The theoretical particle called graviton9 is in conversation but has not been detected, and therefore we cannot use the SM to explain the properties of the gravitational force on quantum scales the way we can with the other 3 forces.

4.3  Matter-Antimatter Asymmetry

In all processes we have seen so far, the creation of a particle means the creation of its antiparticle (the lepton conservation law for example)9, and when they meet annihilation happens. It would be logical to assume that when the universe formed the same happened. However, in reality, we live in a universe that is heavily dominated by matter and the main question is ‘why? What changed the balance?’

4.4 Neutrino Oscillation Problem

The neutrino oscillation problem is the fifth problem of the SM and the main focus of this paper.

In this paper, ‘oscillation’ is defined as the ability of a particle to switch between flavours (see Section 3.2 for more details).

For a particle to be able to oscillate, it must have mass10. In the SM, neutrinos (as all fermions) are considered to be Dirac particles; therefore, recall from Section 3.6 that they need both right- and left-handed versions to acquire mass.

However, all data available to us at the moment states that only left-handed neutrinos exist in our universe today11. Thus, neutrinos should not be able to interact with the Higgs field, and therefore be massless, producing zero oscillations.

However, experiments consistently detect neutrino oscillations, leading to neutrino oscillation problem which poses the simple question of ‘How’.

5. The Seesaw Theory: A Solution to the Neutrino Oscillation Problem

There are many theories that speak of physics beyond the SM and explain neutrino oscillation. The two theories presented here are the most researched and popular in the scientific community. One proposes different mechanisms that would allow neutrinos to obtain mass, and the other speaks of an option that makes neutrino oscillation possible even without mass

5.1  Majorana vs. Dirac Particles

Sterile neutrino is a theoretical right-handed neutrino that interacts only through gravity8, the name Sterile is due to the fact that it is almost undetectable.

The reason why the existence of Sterile Neutrino is supposed to be likely is the fact that all other fermions have been observed to have both right and left chirality10, so it is logical to suppose the same for neutrinos.

For the mass solution, the sterile neutrino seems to be the answer, no matter if it is Dirac or Majorana neutrino.

Although Dirac particles have distinction between particles and antiparticles and have charge, the Majorana particle is its own antiparticle (right-handed) and has zero charge (because it is both a particle and its antiparticle)12.

If the sterile neutrino turns out to be a Dirac particle, neutrinos obtain their mass through the Higgs mechanism8.

Being right-handed, the sterile neutrino makes interaction of neutrinos with the Higgs field possible, therefore, detectable neutrinos can obtain mass through the Higgs mechanism and oscillate.

If sterile neutrino is a Majorana particle, the seesaw mechanism naturally makes six existing neutrino fields behave as Majorana fields8, making three of them high-mass and others three low-mass, creating Higgs-like mechanism of obtaining mass8.

The appeal of the second approach is that it naturally explains why masses of detectable neutrinos are so low. Moreover, it also means violation of the Lepton Conservation Law which can be an explanation of other SM problems such as the Matter Antimatter Asymmetry8. One of the experiments for detecting Majorana neutrinos is aimed at this violation.

Double beta decay is a radioactive decay that produces neutrino and its antineutrino13. If we are ever to detect neutrinoless double beta decay it would mean that the neutrino that was produced by this reaction is both a particle and its antiparticle, Majorana neutrino13. It is important to understand that even if sterile neutrino is a Majorana particle, statistical occurrence of neutrinoless double beta decay would have a really small probability, therefore all average double beta decays do not disprove the theory. The established half-life of it is 1015 times the age of universe14.

5.2  Seesaw Mechanism

There are three types of seesaw mechanisms. All of them suppose the existence of neutrinos with Dirac and additional masses and explain lightness of observed neutrinos with interplay between two masses15.

The name seesaw comes from the mathematical model that states that sterile neutrinos with large Majorana mass ‘elevate’ detectable neutrinos, allowing them to have such a small mass16.

5.3  Type 1 seesaw mechanism

Type 1 seesaw model is the simplest in understanding and math.

This model proposes the existence of light neutrinos for all three neutrino flavors and corresponding right-handed heavy neutrinos with large Majorana mass16. These Majorana masses are introduced through this matrix:

(1)   \begin{equation*}M_\nu =\begin{pmatrix}0 & m_D \\m_D^T & M_R\end{pmatrix}\end{equation*}

12’16’17

where:

  • mD – Dirac mass term,
  • MR – Majorana mass,
  • mν – mass of detectable neutrinos. This leads to Light neutrino mass being:

(2)   \begin{equation*}m_\nu \sim \frac{m_D^2}{M_R}\end{equation*}

16’17

After introducing right-handed Majorana neutrinos, the Higgs field acquires a vacuum expectation value (vev) v = 246 GeV18 and the Dirac mass becomes:

(3)   \begin{equation*}m_D = f v\end{equation*}

16’17

The effective light neutrino mass is:

(4)   \begin{equation*}m_\nu \sim \frac{m_D^2}{M_R} = \frac{f^2 v^2}{M_R}\end{equation*}

16’17

mD is a Dirac mass that exists at electroweak scale (∼ 246 GeV) and MR is Majorana mass that exists at GUT scale (∼ 1014 – 1015 GeV)17, meaning that in equation 4 divider is many times grander than dividend, making the resulting quotient mv (mass of detectable neutrinos) especially light (∼0.1 DeV).

This model explains many orders of magnitude smaller than other fermion masses. 

5.4  Type 2 seesaw mechanism

Type 2 seesaw mechanism introduces a scalar Higgs triplet ∆16, which directly introduces lepton number violation.

In type 2 seesaw mechanism neutrinos obtain Majorana mass through Yukawa coupling Y∆ between the scalar triplet and the SM lepton doublets L16.

The scalar triplet acquires a vev v∆, generating the neutrino mass:

Type 2 seesaw mechanism

(5)   \begin{equation*}m_\nu = Y_{\Delta} v_{\Delta}\end{equation*}

16’17
The vev v\Delta is suppressed by the heavy mass M\Delta of the scalar triplet:

(6)   \begin{equation*}v_{\Delta} \sim \frac{\mu v^2}{M_{\Delta}^2}\end{equation*}

16’17
where:

\mu – dimensional coupling constant,
v – SM Higgs vev (v \sim 174 GeV).

Substituting v_{\Delta} (with 5) into neutrino mass equation:

(7)   \begin{equation*}m_\nu \sim Y_{\Delta} \frac{\mu v^2}{M_{\Delta}^2}\end{equation*}

16’17

This model provides an alternative framework for neutrino mass generation without requiring heavy right-handed neutrino and predicts testable collider phenomena.

This model provides an alternative framework for neutrino mass generation without requiring heavy right-handed neutrino and predicts testable collider phenomena.

5.5 Type 3 seesaw model

The model introduces heavy fermion triplets T instead of scalar triplets or right-handed neutrinos16.

(8)   \begin{equation*}M_\nu \sim \frac{m_D^2}{M_T}\end{equation*}

16’17’19

where:

  1. MT – mass of fermion triplets.

The neutrino mass arises from Yukawa coupling h between the fermion triplets and the SM lepton doublets. This breaks the electroweak symmetry and Dirac mass becomes:

(9)   \begin{equation*}m_\nu \sim \frac{m_D^2}{M_T} = \frac{h^2 v^2}{M_T}\end{equation*}

16’17’20

The Type 3 seesaw model is much higher in energy than the previous two, so its predictions are supposed to be easier to detect.

5.4  Seesaw model conclusion

  • Type 1 model: Type 1 model focuses on right-handed neutrinos and their heavy Majorana masses, addressing the origin of light neutrino masses through the seesaw effect.
    • Type 2 model Type 2 model introduces scalar triplets to directly couple to lepton doublets, offering a mechanism distinct from right-handed neutrinos.
    • Type 3 model: Type 3 model replaces scalar triplets with fermion triplets, bridging gaps in high-energy physics and providing new testable predictions.

Each model reflects different extensions of the SM and offers insights into neutrino mass generation, lepton number violation, and high-energy scales.

6. Lorentz Violation: A Different Proposed Solution

Some scientists believe that there are options in which a neutrino can oscillate regardless of whether or not it has mass. One of the most popular alternative approaches is the Lorentz violation theory. The main idea of the theory is that Lorentz transformations (the core equations of Einstein’s relativity theory and SM) are not completely correct. It is thought that in some conditions a violation of these transformations occurs that allows neutrinos to oscillate regardless of the mass.

6.1  Lorentz symmetry

Lorentz symmetry (what Lorentz violation violates) is math in base of the modern general relativity.

General relativity came in place of Newtonian relativity when the invariance of the speed of light was discovered21. General relativity merges space and time, making length and time to not be the same in different frame of references21. Lorentz transformation (Lorentz symmetry) is math model that predicts changes of them in different frames of work21.

6.2 Basic terminology

These are some terms which one needs to understand for this topic.

  • Lorentz Invariance: Lorentz Invariance is a physics principle that states that rules of physics work the same way in any inertial framework21.
    Lorentz Violation: Lorentz Violation is the idea that in some circumstances the Lorentz invariance principle and symmetry it creates are violated, stop working the way they are thought to21.
    • Hamiltonian: the total energy of a system (both kinetic and potential)21.

This is a term which is not present in this paper but is most likely to be met if one continues reading more works on the topic.

  • PMNX mixing matrix: Linear algebra matrix that is used to calculate the probability of the change in neutrino flavour21.

6.3  Introduction to the Lorentz Violation

Lorentz violation theory has been on minds of scientists for a long time now. One of the most known motivation for it is String theory, tensor fields of which are coupled to the tensor vevs and, therefore, depend on directions and velocities of fields coupled with these vevs22. It is important to understand that Lorentz-violating effects must be really small22, so absence of experimental evidence does not disprove the theory and is due to our limited technological capabilities.

For instance, the probability of neutrino oscillation in Lorentz violation model is calculated that way:

(10)   \begin{equation*}\frac{\Delta m^2 L}{4E}\end{equation*}


where:

  • ∆m2 – the difference between 2 neutrino flavours. The larger the difference, the faster the oscillations occur.
  • L – distance the neutrino has traveled.
  • E – energy of the neutrino.

In the math models, Lorentz violation (if it’s proved) is supposed to exist as extra terms added to the Lagrangian and Hamiltonian energy equations22.

Modern experiments on Lorentz violation aim to detect these additional terms. The following sections are to go over three different models of Lorentz Violation.

6.4 The Coleman-Glashow model (C-G)

The C-G model is one of the earliest theories for introducing Lorentz Violation. This model uses modified Lagrangian math that is not Lorentz-invariant across all frames of reference, remaining invariant only in one preferred reference frame23.

C-G model introduces different maximum attainable velocities for different particles, providing a simple trackable way to break down Lorentz Violation24.

Due to lack of full frame independence C-G model is better understood as a limited phenomenological tool instead of complete theory23.

C-G model is useful in analyzing how Lorentz Violation might appear in specific experiments, but it cannot describe effects of Lorentz Violation consistently across different frames23. The following models aim to address this limitation.

6.5 The Minimal SM Extension (SME)

The minimal SME extends the SM by providing an opportunity to include needed Lorentz-violating terms by hand23. In contrast to simpler models like C-G, the SME does not assume space and time to be the same in all directions and for all observers. It allows for small violations of these symmetries to be put directly into math of SM25.

To make this possible, SME introduces specialized background fields that can interact with particles. These fields function as fixed backgrounds that do not change inside single observer’s frame but transform switching between different frames23. Due to this, SME treats the frame in which fields look “unchanging” as special, it being sometimes called “new either” or “vacuum at rest”23. In SME, Lorentz Violation does not happen the same way everywhere. It presents as some particles acting slightly differently depending on how they move through background fields24.

SME framework is useful for exploring what experimental signatures of Lorentz Violation might look like, for example, tiny differences in the behavior of particles moving in different directions24. It works optimally in flat spacetime, but in curved spacetime (like near black hole) behavior of these violations could become more complicated23.

While SME is effective for testing ideas and making predictions it does not explain how Lorentz Violation would exist in the first place, for that goal more fundamental models like SM Supplement are needed23.

6.6 The SM Supplement (SMS)

The SMS aims to provide a more fundamental theoretical foundation for Lorentz Violation. In the SMS framework the Lorentz violation terms are brought about from a basic principle denoted as the physical independence or physical invariance23. Instead of inserting violation terms by hand as in SME, SMS introduces them as a consequence of requiring that the laws of physics remain form-invariant under changes of reference frames, even when those frames are not related by Lorentz symmetry23.

The SMS framework can be understood as a combination of these three scenarios:

  1. So called fixed scenario, an approximation in like C-G model, where the observer focuses on the effects of Lorentz violation within one frame not caring for relations with other frames23.
  2. Also called ‘new ether’ scenario in which Lorentz Violation matrices act as tensor fields between different frames and remain constant within one fame (similar to background fields in SME)23.
  3. Can be called covariant scenario. In this scenario Lorentz Violation matrices and their corresponding SM particles transform as tensors, allowing for more unified treatment (this means that these matrices are emergent and covariant with their SM particles). Note that such scenario still needs to be checked for consistency when applied26.

7. Seesaw vs. Lorentz Violation

 SeesawLorentz Violation
Energy level\sim 10^{10}-10^{15} \text{GeV}183.00 \times 10^{17} \ \text{GeV}27
Approach to oscillationSeesaw implies existence of undetected particlesLorentz Violation predicts energy-dependent oscillation anomalies

8. Experiments on Neutrino Oscillation

Though this is theoretical paper, here are some breath overviews of modern experiments on the subject.

8.1 Neutrinoless Double Beta Decay

  • Neutrinoless double beta decay (so far) is currently the most prominent experimental approach to testing the existence of Majorana neutrinos13. The specifics of it were already explained in the end of section 5.1, but additional information can be found in this paper13.

Search for neutrinoless double-beta decay (0\nu \beta \beta) obtains 0\nu \beta \beta decay half-time and through formula

(11)   \begin{equation*}T_{1/2} \propto |m{\beta\beta}|^2\end{equation*}

(the decay rate is inversely proportional to the square of the effective Majorana mass) helps to determine effective Majorana neutrino mass ranges.

At the moment, search for neutrinoless double-beta decay has already helped to exclude some ranges of Majorana mass. For example, KamLAND-Zen experiment gave upper limits of the effective Majorana neutrino mass in range 28-122 meV28. Future experiments that are listed below aim to push those range limits even farther.

8.2  nEXO

nEXO is an ongoing experiment searching for neutrinoless double beta decay. It is designed to extend knowledge of this decay to a level of 1028 or even 1029 times the age of universe (current is only 1015 as already said in section 5.1)14. The experiment introduces new components to the classical experiment such as ultra-high vacuum, cryogenics and new versions of old mechanics and electronics14.

8.3 IceCube

IceCube Neutrino Observatory is an observatory located on the South Pole29. It addresses the nature of both neutrinos and dark matter. Icecube experiments work towards both seesaw models30 and Lorentz Violation31. This is the first and so far only cubic-kilometer neutrino telescope29. The project turned  a cubic kilometer of Antarctic ice into a detector that observes neutrinos from GeV to PeV energy. The IceCube detected the first high-energy astrophysical neutrino flux32. For more information on achievements of it read32.

8.4 SNO+

SNO+ also searches for neutrinoless double beta decay and is located 2km underground in Canada. It is a liquid scintillator detector (organic liquid that lights when charged particles go through it)33. SNO+ introduces new generation of liquid scintillator that is times safer to handle and more environmentally friendly. The most relevant results of SNO+ experiment can be seen here34.

9. Conclusion

Neutrino oscillation has been ongoing problem for a long time and requires new generations of scientists to pay more attention to it. This paper is a good introduction not only to this particular topic, but to the field of particle physics overall.

This paper provides understanding of the standard model, explains quantum numbers, chirality, basics of Higgs mechanism and limitations of SM. It talks about basic math of the three seesaw models, models of Lorentz violation and experiments regarding all of it.

Each extension to the SM, such as seesaw mechanisms and Lorentz violation theories, offers insights into unresolved phenomena of both neutrino oscillation and matter-antimatter asymmetry. Continued exploration will refine our understanding of the universe.

Last chapter that summarizes experiments regarding the subject is kind of a list of recommended fields of interest for those who want to learn more about experimental part of the subject. This paper is limited to theoretical side of it and balancing of combining complex subject with easily-understandable language.

References

  1. Glen Elert. The Standard Model. url: https://physics.info/standard/ [↩] [↩] [↩] [↩] [↩] [↩]
  2. CERN. The Standard Model. url: https://www.home.cern/science/physics/ standard-model [↩] [↩] [↩]
  3. R. Mann. An Introduction to Particle Physics and the Standard Model. Taylor & Fran- cis, 2010. isbn: 9781420083002 [↩] [↩] [↩] [↩] [↩]
  4. Chemistry Learner. Quantum Numbers. url: https://www.chemistrylearner.com/ quantum-numbers.html [↩] [↩]
  5. David J. Griffiths. Introduction to Quantum Mechanics. Prentice-Hall, 1994. Isbn: 9781107189638 [↩]
  6. LibreTexts Physics. Particle Conservation Laws. url: https://phys.libretexts. org/Bookshelves/University_Physics/University_Physics_(OpenStax)/University_   Physics_ III_- _Optics_ and _ Modern _ Physics_ (OpenStax )/11 % 3A _ Particle_ Physics_and_Cosmology/11.03%3A_Particle_Conservation_Laws [↩] [↩] [↩] [↩] [↩] [↩]
  7. LibreTexts Chemistry. Chiral Molecules. url: https : / / chem . libretexts . org / Bookshelves/ Organic_Chemistry/ Map: _Organic_Chemistry_(Vollhardt_and_ Schore)/05._Stereoisomers/5.1:_Chiral Molecules [↩]
  8. Albert Forsyth Daneri.   Imperial College London. The Seesaw Mechanism Legacy, The Root of Neutrino Masses and Leptogenesis. 2023 [↩] [↩] [↩] [↩] [↩] [↩]
  9. Oscar Miyamoto Gomez. Five Mysteries the Standard Model can’t Explain. url: https: //www.symmetrymagazine.org/article/five-mysteries-the-standard-model-  cant-explain [↩] [↩] [↩] [↩]
  10. Dhananjay Saikumar. University of St Andrews. Exploring the Frontiers: Challenges and Theories Beyond the Standard Model. 2024 [↩] [↩]
  11. Dhananjay Saikumar. University of St Andrews. Exploring the Frontiers: Challenges and Theories Beyond the Standard Model. 2024 [↩]
  12. Albert Forsyth Daneri. Imperial College London. The Seesaw Mechanism Legacy, The Root of Neutrino Masses and Leptogenesis. 2023 [↩] [↩]
  13. Alberto Garfagnini. “Neutrinoless Double Beta Decay Experiments”. In: International Journal of Modern Physics: Conference Series 31.1460286 (2014). doi: https://doi. org/10.1142/S2010194514602865 [↩] [↩] [↩] [↩]
  14. nEXO. nEXO Overview. url: https://nexo.llnl.gov/nexo-overview [↩] [↩] [↩]
  15. CMS Collaboration. CERN. Two Ends of a Seesaw. url: https://cms.cern/news/ two-ends-seesaw [↩]
  16. Soumita Pramanick. “Ameliorating the Popular Lepton Mixing with A4 Symmetry: A Seesaw Model for Realistic Neitrino Masses and Mixing.” In: Physical Review D 98.075016 (2018). doi: https://doi.org/10.48550/arXiv.1711.03510 [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
  17. Goran Senjanovi´c and Vladimir Tello. “Disentangling the Seesaw Mechanism in the Minimal Left-right Symmetric Model.” In: Physical Review D 100.115031 (2019). doi: https://doi.org/10.1103/PhysRevD.100.115031 [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
  18. Albert Forsyth Daneri. Imperial College London. The Seesaw Mechanism Legacy, The Root of Neutrino Masses and Leptogenesis. 2023 [↩] [↩]
  19. Alessandro Strumia Roberto Franceschini Thomas Hambye. “Tupe-III See-saw Mechanism at CERN LHC.” In: Physical Review D 78.033002 (2008). doi: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.78.033002 [↩]
  20. Alessandro Strumia Roberto Franceschini Thomas Hambye. “Tupe-III See-saw Mechanism at CERN LHC.” In: Physical Review D 78.033002 (2008). doi: https:// journals.aps.org/prd/abstract/10.1103/PhysRevD.78.033002 [↩]
  21. Robert Resnick. Introduction to Special Relativity. John Wiley & Sons Canada, Limited, 1968. isbn: 9780471717249 [↩] [↩] [↩] [↩] [↩] [↩] [↩]
  22. Jorge S. Diaz. “Overview of Lorentz Violation in Neutrinos”. In: Proceedings of DPF- 2011, Providence, RI (2011). doi: https://arxiv.org/abs/1109.4620 [↩] [↩] [↩]
  23. Bo-Qiang Ma. “New Chances for Research on Lorentz Violation”. In: International Journal of Modern Physics: Conference Series 10 (2012), pp. 195–206. doi: https: //doi.org/10.1142/S2010194512005910 [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
  24. V. Alan Kostelecky. “Gravity, Lorentz Violation, and the Standard Model.” In: Physical Review D 69.105009 (2003). DOI: 10.1103/PhysRevD.69.105009 [↩] [↩] [↩]
  25. D. Colladay and V. Alan Kostelecky. “Lorentz-Violating Extension of the Standard Model.” In: Physical Review D 58.116002 (1998). DOI: https://doi.org/10.1103/PhysRevD.58.116002 [↩]
  26. Bo-Qiang Ma. “New Chances for Research on Lorentz Violation”. In: International Journal of Modern Physics: Conference Series 10 (2012), pp. 195–206. doi: https://doi.org/10.1142/S2010194512005910 [↩]
  27. Hanlin Song and Bo-Qiang Ma. “Lorentz Invariance Violation from Gamma-Ray Bursts.” In: Astrophys.J. 983(2025) 9. DOI: https://doi.org/10.48550/arXiv.2504.00918 [↩]
  28. S.Abe and others. “Search for Majorana Neutrinos with the Complete KamLAND-Zen Dataset.” In: arXiv2406.11438. DOI: https://doi.org/10.48550/arXiv.2406.11438 [↩]
  29. IceCube. Ice Cube. url: https://icecube.wisc.edu/science/icecube/ [↩] [↩]
  30. Thede de Boer, Raffaela Busse, Alexander Kappes, Michael Klasen,, and Sybrand Zeinstra. “New constraints on radiative seesaw models from IceCube and other neutrino detectors.” In: Phys. Rev. D 103, 123006 (2021). DOI: https://doi.org/10.1103/PhysRevD.103.123006 [↩]
  31. Barbara Skrzypek, Carlos A. Argüelles. “Lorentz Violation in Neutrino Oscillations using IceCube Atmospheric Neutrino Interferometry.” In: arXiv:2302.08998v1. DOI: https://doi.org/10.48550/arXiv.2302.08998 [↩]
  32. IceCube.  Research   Highlights.  url:  https://icecube.wisc.edu/science/research/ [↩] [↩]
  33. Snoplus. About SNO+. url: https://snoplus.phy.queensu.ca/about.html [↩]
  34. Snoplus.  Results.  url: https://snoplus.phy.queensu.ca/results.html [↩]

RELATED ARTICLESMORE FROM AUTHOR

LEAVE A REPLY

Please enter your comment!
Please enter your name here