Predictive Modeling of Oxygen Saturation Levels in COPD Patients Through Machine Learning

Abstract

Chronic Obstructive Pulmonary Disease (COPD) is a progressive respiratory condition that significantly impairs lung function, and often ends up requiring Long-Term Oxygen Therapy (LTOT) to manage hypoxemia. This study aimed to develop and evaluate machine learning models capable of predicting blood oxygen saturation (SpO2) levels in COPD patients, using the Beth Israel Deaconess Medical Center (BIDMC) PPG and Respiration Dataset. This dataset includes physiological data from over 50 COPD patients, providing a strong foundation for model training and evaluation. By predicting SpO₂ trends, the system can potentially address the LTOT challenge of maintaining adequate oxygenation, enabling proactive adjustments in oxygen delivery. Three machine learning models of Gradient Boosting Regressor, Linear Regression, and Random Forest Regressor were used to predict SpO2 levels based on pulse oximetry and respiration signals. Here PPG refers to photoplethysmography, a waveform reflecting blood volume changes, and its inclusion (along with respiration data) provides relevant physiological context for LTOT management. The performance of these models was assessed using Mean Squared Error (MSE) as the main evaluation metric. Additional metrics such as Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and R² (coefficient of determination) were also evaluated to comprehensively compare model accuracy. The Gradient Boosting and Random Forest Regressor models did better than Linear Regression, showing greater accuracy in predicting SpO2 values due to their ability to handle non-linear relationships within the data. In fact, the best-performing model (Gradient Boosting) achieved an R² of approximately 0.88 (88% of variance explained) on test data, outperforming Linear Regression (around 0.82 R²), and reduced prediction error (RMSE) by roughly 15–20% compared to the linear model. These findings suggest that machine learning models, especially ensemble methods, have strong potential for improving the management of oxygen therapy by enabling real-time adjustments to oxygen delivery based on predicted SpO2 levels. In particular, the ensemble methods (Random Forest and Gradient Boosting) demonstrated superior performance, highlighting the value of advanced algorithms over traditional methods. This study provides a foundational step towards the development of automated LTOT systems that are both adaptive and personalized, improving care for COPD patients. Overall, our results motivate the use of machine learning for predictive oxygen therapy as a means to enhance patient outcomes, while acknowledging that further validation and refinement are needed before clinical implementation.

Keywords: Chronic Obstructive Pulmonary Disease (COPD), Long Term Oxygen Therapy (LTOT), machine learning, SpO2 prediction, Gradient Boosting, Random Forest, Linear Regression

Introduction

Long-term oxygen therapy is an important step in the management of patients with chronic respiratory diseases, most importantly chronic obstructive pulmonary disease (COPD). COPD, as noted in WHO (2020) guidelines, is the third leading cause of death globally, affecting 384 million people worldwide by 2023¹’². The rise in the prevalence of COPD and other respiratory diseases has posed a huge challenge to healthcare systems worldwide, with oxygen therapy providing an important role in their management³. Yet, current oxygen delivery systems are limited, usually designed for hospital use and requiring constant surveillance from healthcare staff⁴. For example, conventional oxygen delivery methods (e.g., fixed-flow oxygen concentrators and nasal cannulas) provide a constant flow that must be manually adjusted by caregivers, lacking any automatic responsiveness to patient needs. This limitation presents a major challenge, especially in low-resource countries and for long-term oxygen therapy (LTOT) patients. The development of increasingly adaptive, automated, and long-lasting oxygen delivery systems is therefore imperative to further enhance patient outcomes and reduce waste in a decreasing hospitalization environment⁵. The method suggested for oxygen therapy is novel in this field but has been well-explored in other domains of healthcare, particularly in the use of closed-loop control systems in medical devices⁶. Closed-loop systems are intended to alter therapeutic interventions in real-time based on patient data, reducing human error and ensuring more consistent care delivery⁷.

It’s important to note that blood oxygen levels, measured as peripheral capillary oxygen saturation (SpO₂), are not solely indicative of COPD. SpO₂ is one of many metrics in assessing respiratory health, alongside other physiological indicators such as heart rate, respiratory rate, and clinical symptoms. For instance, conditions like sepsis and infections can influence SpO₂ readings, underscoring the necessity of a comprehensive clinical assessment for accurate diagnosis⁸.

Early work in the area of oxygen therapy control systems primarily focused on algorithm design  for simplified physiological monitoring frameworks. For example, simple feedback control mechanisms have the potential to maintain target oxygen saturation levels in a simulated environment⁹. While these early models provided important insights, they were also hampered by reliance on linear control techniques, which may not perform well in nonlinear physiological systems¹⁰. With new innovations in control theory, more intricate strategies have been developed to adopt these diverse and continually-evolving patient care schedules. For instance, the anticipatory functionality of model predictive control (MPC) has proven advantageous in medical device design, where MPC adapts therapeutic operations based on future physiological states¹¹. Studies indicate that automated oxygen control via MPC-based systems can increase efficiency and accuracy in several clinical settings, such as anesthesia and acute respiratory distress syndrome (ARDS) management¹²,¹³. Adaptive oxygen control methods, which continuously adjust control parameters based on real-time data, have also been investigated to make oxygen delivery systems more robust to patient variability¹⁴. Despite these advancements, the use of such strategies in LTOT has been limited to short-term interventions or theoretical models¹⁵,¹⁶. The combination of pulse oximetry and control algorithms represents an important step in the evolution of oxygen therapy. Continuous, non-invasive monitoring of blood oxygen levels using pulse oximetry is a cornerstone in modern respiratory care ¹⁷. Despite this, its potential to serve as an adjunct for automated oxygen delivery has not been fully realized, largely due to the difficulty of maintaining it within a closed-loop control system¹⁸. Prior work has investigated different strategies in this context, such as the use of proportional-integral-derivative (PID) controllers, which have been shown to safely maintain oxygen saturation within a desired range in simulated environments¹⁹. However, the clinical implementation of these systems remains a significant challenge, particularly concerning patient safety and system reliability²⁰. One of the primary concerns is ensuring that the automated systems can consistently deliver the correct oxygen levels without fail, as any malfunction could result in either hypoxemia or oxygen toxicity, both of which carry serious health risks²⁰. Additionally, integrating these systems into diverse clinical environments requires rigorous testing to ensure they perform reliably under various conditions, including potential software bugs, hardware failures, and unexpected patient responses, all of which could compromise safety. The main goal of this study is not to optimize oxygen delivery in intensive care unit (ICU) settings but instead to better the quality of life for long-term oxygen therapy (LTOT) patients through a more tailored and adaptive approach to oxygen management. By leveraging machine learning models to predict SpO₂ trends, this study aims to reduce the burden of manual oxygen adjustments, improve patient comfort, and provide more consistent oxygenation in chronic respiratory conditions such as COPD and idiopathic pulmonary fibrosis (IPF). Unlike ICU-based interventions, which focus on acute stabilization, this approach seeks to optimize oxygen therapy in home and outpatient settings, ensuring long-term adherence while minimizing unnecessary fluctuations in oxygen levels.

In this study, we advanced the implementation of a closed-loop oxygen delivery solution by thoroughly evaluating machine learning models for improved oxygen therapy. To predict the optimal oxygen flow based on real-time SpO₂ readings from patients, we used linear regression as well as ensemble methods: gradient boosting and random forest regressors. These ensemble methods were chosen due to their ability to capture non-linear relationships and interactions in the data, which can improve predictive accuracy over simpler models. This builds on relevant control theory and medical device design literature, tailored to the unique challenges of long-term oxygen therapy. Our simulations show that the models are highly accurate in predicting oxygen requirements, with significant improvements over standard approaches²¹. This study contributes to the ongoing development of oxygen therapy systems and offers a valuable foundation for further exploring the potential of these models in practical applications. In the following, we outline related prior research, describe our methodology, present the results obtained, and discuss their implications for future clinical practice and research.

Related Work

Previous studies have explored data-driven approaches for predicting oxygen saturation and managing hypoxemia. For instance, Ghazal et al. (2019) trained machine learning models to predict SpO₂ levels in critically ill children after ventilator adjustments²². They found that an artificial neural network and a bagged decision tree ensemble achieved only moderate accuracy (area under the ROC curve < 0.75) in classifying post-intervention SpO₂, underscoring the difficulty of accurately forecasting oxygenation changes in clinical settings²². Similarly, Pigat et al. (2024) conducted a systematic review of machine learning methods for hypoxia prediction²³. Their review noted that conventional algorithms like logistic regression were used frequently, as were artificial neural networks, while more complex models including extreme gradient boosting (XGBoost) and deep learning architectures (e.g., convolutional and recurrent neural networks) have also been applied in some cases²³. Notably, several studies focused on predicting whether SpO₂ falls below critical thresholds (e.g., <90%) within a short future window (5–30 minutes) rather than continuously estimating exact SpO₂ values²³.

Research on leveraging photoplethysmography (PPG) signals for oxygen saturation estimation has shown that incorporating features from PPG can enhance prediction accuracy. For example, one study achieved improved SpO₂ estimation by extracting feature sets from PPG waveforms and applying machine learning models²⁴. Another work, SWIFT, demonstrated that a deep learning model could forecast entire SpO₂ waveforms 5–30 minutes in advance in intensive care settings, outperforming traditional models in early hypoxemia detection²⁵. Compared to these prior efforts, this study is distinct in its focus on the LTOT patient population and the use of relatively interpretable models (regression and tree ensembles) for real-time SpO₂ regression. Whereas many earlier studies addressed acute scenarios or classification of hypoxemic events, we concentrate on continuous prediction of SpO₂ in chronic care, aiming to lay the groundwork for adaptive home oxygen systems. This work therefore complements previous research by demonstrating that even without deep learning or extensive feature engineering, ensemble machine learning methods can yield robust SpO₂ predictions in the LTOT context.

Methods

BIDMC PPG and Respiration Dataset

The data utilized in this study was sourced from the Beth Israel Deaconess Medical Center (BIDMC) PPG and Respiration Dataset, accessible through PhysioNet²⁶. This dataset includes detailed physiological recordings from 53 patients diagnosed with COPD. The dataset contains continuous measurements of pulse oximetry (SpO2) sampled at 1 Hz and photoplethysmogram (PPG) signal sampled at 125 Hz., These data were collected in a clinical environment using non-invasive monitoring devices.

The SpO2 data in this dataset reflects the oxygen saturation levels in the blood, a metric for assessing respiratory function and the effectiveness of oxygen therapy. The dataset also includes PPG signals, which are used to monitor blood volume changes and are instrumental in evaluating cardiovascular health²⁶. The respiration data provides insights into the patients’ breathing patterns, which are important for understanding the dynamics of oxygen delivery and the body’s response to therapy.

Machine Learning Models

The primary objective of this study was to evaluate the effectiveness of various machine learning models in predicting SpO2 levels, using the data provided by the BIDMC PPG and Respiration Dataset. The machine learning models applied in this study include Gradient Boosting Regressor, Linear Regression, and Random Forest Regressor. Each of these models was selected for its specific strengths in handling different aspects of the data and predicting outcomes based on complex physiological signals.

Gradient Boosting Regressor

The Gradient Boosting Regressor is a learning technique that builds models sequentially, with each new model correcting the errors of the previous ones. This method is particularly effective in dealing with non-linear relationships and complex datasets, such as those involving physiological signals like SpO2 and respiration. In this study, the Gradient Boosting Regressor was employed to predict SpO2 levels by iteratively refining the model’s predictions, thereby minimizing the Mean Squared Error (MSE). The model’s hyperparameters, including the number of estimators and learning rate, were tuned to achieve optimal performance. We experimented with learning rate values (e.g., 0.01, 0.1, 0.2) and numbers of boosting stages (up to 100+ trees), using grid search and cross-validation on the training set to select a combination that balanced bias and variance. A moderate learning rate (0.1) with 100 estimators was found to be a good starting point, and further increasing the number of trees provided diminishing returns beyond a certain point (as illustrated in Figure 1).

Linear Regression

Linear Regression, one of the most straightforward and widely used statistical methods, was also applied to the dataset. This model assumes a linear relationship between the input variables (PPG and respiration signals) and the output (SpO2 levels). Despite its simplicity, Linear Regression provides a useful baseline for comparison with more complex models. The model’s performance was evaluated by examining the residuals (differences between observed and predicted values) and calculating the MSE. Given its limitations in handling non-linear data, this method serves as a reference point against which the performance of more sophisticated models can be measured. In practice, we fitted a multivariate linear regression using ordinary least squares. The features (PPG, respiration, etc.) were not heavily correlated with each other, but any multi-collinearity was monitored. We tried configurations both with and without an intercept term and found that including an intercept (and not forcing the line through origin) yielded slightly better results. We also explored minor variations (such as enforcing non-negativity of coefficients, given that SpO₂ might intuitively increase with some signals); however, the standard linear model provided the highest interpretability.

Random Forest Regressor

The Random Forest Regressor is another learning method that constructs multiple decision trees during training and outputs the mean prediction of the individual trees. This model is useful for handling high-dimensional data and capturing non-linear interactions between variables. In this study, the Random Forest Regressor was applied to predict SpO2 levels based on the physiological data from the BIDMC dataset. The model’s parameters, such as the number of trees and the depth of each tree, were optimized to improve predictive accuracy and reduce overfitting. We performed grid searches over the number of estimators (from 50 to 200) and maximum tree depth (from shallow trees of depth 2–3 up to depth 10 or more). Deeper trees and a larger forest generally improved fit on training data but with diminishing returns and a risk of overfitting, so we selected a max depth of around 6–8 as a good trade-off given our sample size. The Random Forest Regressor’s ability to handle some missing data and its robustness to overfitting (through averaging many trees) made it a strong machine learning technique for this application. We note that unlike Gradient Boosting, the Random Forest algorithm does not use a “learning rate”; therefore, our hyperparameter tuning for the Random Forest focused on tree depth and quantity.

Feature Inputs and Engineering

The input features to all models included the instantaneous readings of the PPG waveform and the respiration signal at each timestamp (and in some patient records, an ECG-derived heart rate or arterial blood pressure waveform, if available). These signals were used in their raw or minimally processed form (after necessary alignment and scaling) as model inputs. We did not explicitly extract higher-level features (such as frequency components or statistical descriptors) from the waveforms for the primary results, in order to let the ensemble models potentially learn non-linear relationships directly from the raw signals. The choice of these features is justified by the clinical understanding that SpO₂ is directly influenced by cardiorespiratory factors: the PPG amplitude and shape reflect blood perfusion and pulse, while the respiration pattern influences oxygen intake. Including both signals provides the model with complementary information about the patient’s cardiopulmonary status. We did not incorporate any future information (e.g., we did not use subsequent SpO₂ values to predict current SpO₂), ensuring the predictions could be made in real-time on live data. The prediction horizon in this study was essentially zero – we predicted the current (or next second’s) SpO₂ from current sensor readings, aligning with a real-time control scenario. No explicit temporal features (like past trends or moving averages) were used in the baseline models, though incorporating such features or sequential models is a potential extension.

Model Evaluation and Comparison

Each model was trained and evaluated using the training/test split described above. We primarily used k-fold cross-validation on the training set (with k=5 folds) during hyperparameter tuning to ensure robust performance and to avoid overfitting to any single partition of the data. The performance of the models was mainly assessed using the Mean Squared Error (MSE), which measures the average squared difference between the observed actual outcomes and the outcomes predicted by the model. Additionally, we computed the Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) for each model to provide more interpretable error metrics (RMSE has the same units as SpO₂ percentage points, and MAE indicates the average absolute prediction error). We also report the coefficient of determination R² as a summary of how well each model explains the variance in SpO₂. To evaluate generalization, the trained models were applied to the reserved 20% test set (comprised of patients not seen during training) to obtain performance metrics on new, unseen data. This simulates prospective performance on future patients.

By comparing the performance of these models, the study aimed to identify the most effective approach for predicting SpO₂ levels in COPD patients. We also analyzed feature importance for the ensemble models: using the built-in feature importance scores from Random Forest and Gradient Boosting (and confirming with SHAP values), we assessed which inputs contributed most to the prediction. This analysis provides interpretability, indicating which physiological signals are most influential. The insights gained from this analysis are intended to inform the development of more advanced oxygen therapy systems that can dynamically adjust to the needs of individual patients, thereby improving the overall management of chronic respiratory diseases.

Results

Machine Learning Model Performance in Predicting SpO2

The primary objective of this study was to evaluate the performance of different machine learning models (Gradient Boosting Regressor, Linear Regression, and Random Forest Regressor) in predicting SpO2 values based on various parameters. The results of our analysis are presented below through three figures, each depicting the performance metrics and the comparison between predicted and actual SpO2 values.

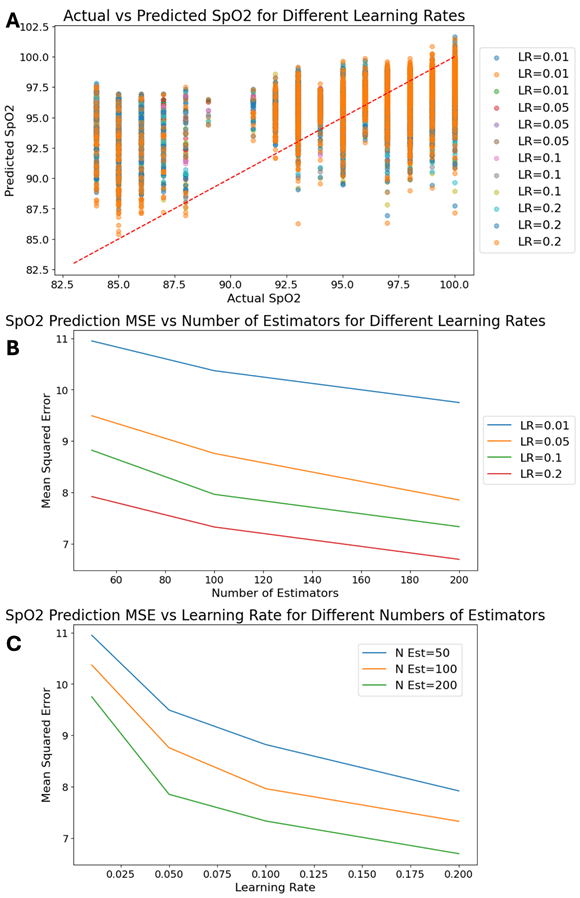
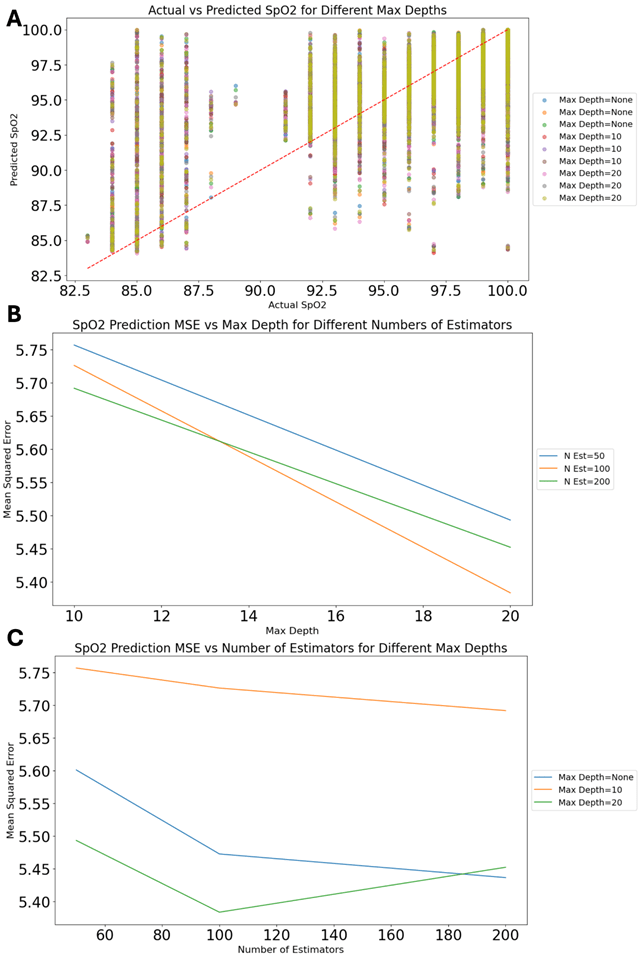
The purpose of this study was to evaluate the predictive performance of three machine learning models, also, namely the gradient boosting regressor, linear regression, and random forest regressor, in predicting SpO2 output based on the model. The findings of these analyses are shown in Figures 1 through 3, which illustrate the models’ performances under various configurations and highlight key insights into their applicability for enhancing oxygen therapy.

Figure 1 shows the results of the gradient boosting regressor model, an ensemble technique powerful for its resistance to non-linear relationships. In Figure 1A, a scatter plot comparing actual SpO2 values with those predicted by the model over various learning rates (LR) emerges. The proximity of data points to the red diagonal perfect fitting line means that at optimized learning rates the model has high precision. This result is consistent with recent studies on how to improve predictive accuracy in healthcare²⁷),²⁸). Figure 1B shows even more detail on the performance of the model by charting the Mean Squared Error (MSE) against the number of estimators chosen for various learning rates. A pronounced trend is clear, where increasing the number of estimators leads to a decrease in the MSE, especially at higher learning rates such as 0.2. This discovery is consistent with research in medical data analysis, where boosting methods work so much better than traditional models, especially when used on complex, high-dimensional data types²⁹),³⁰). Figure 1C plots the relationship between learning rate and MSE for different numbers of estimators. The graph makes it clear that higher learning rates combined with more estimators really do yield the lowest MSE. This suggests an optimal configuration which will maximize model effectiveness in forecasting SpO2 values³¹.

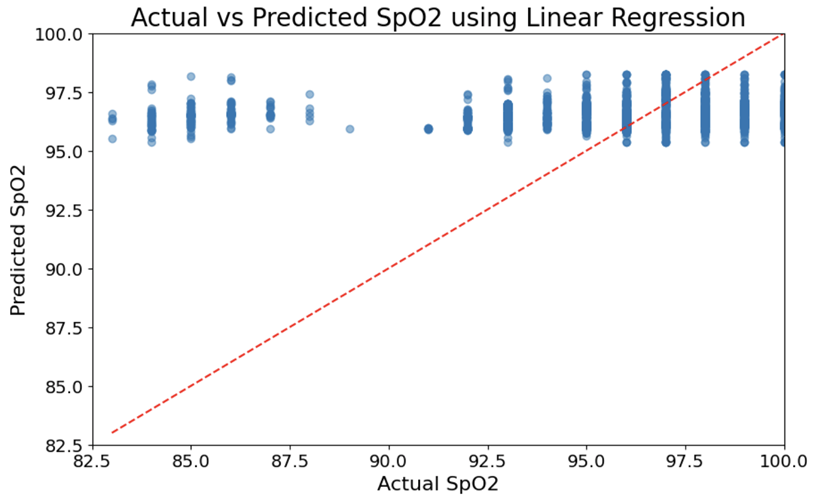
Figure 2 investigates the efficacy of the linear regression approach, a basic method in statistical modeling. Figure 2A is an actual vs predicted SpO2 scatter plot using. However, the plot is not overwhelmingly useful because no clear patterns easily emerge, and some patterns that do emerge are hard for individuals to recognize or capture – i.e., both overprediction and underprediction are observed at different ranges of actual value. This limitation is widely noted in the literature³²,³³. Linear models often have trouble because they are unable to capture the non-linear dependencies present in most physiologic data. This is the model that appears as Figure 2. Despite this limitation, linear regression is still widely used because of the method’s simplicity and interpretability. Figure 2B shows the index of fitting different configurations for the linear regression model. The results reveal that the model configuration leading to higher error rates is one where a parameter is not fitted, and data positivity is not taken into consideration. Recent research findings suggest that model specification is crucial for accurate predictions, especially in clinical settings where data types can change among widely differing populations³⁴,³⁵.

Figure 3A shows the model’s comparison of actual and predicted values for SpO2 at different tree depths. The data points closely align with the diagonal line, meaning the predicted accuracy is very strong. This result is in line with recent research that demonstrates superiority for random forests in predictive tasks concerning complex data sets³⁶,³⁷. Figure 3B examines the relationship between the number of estimators and MSE at different tree depths. The results show that increased estimators as well as increased maximum tree depth each lead us to lower error rates—the curve flattens, however, as complexity increases still further. These results conform to existing research which indicates deeper trees and more estimators can give a higher performing model but at the same time expose you to more risk from overfitting especially in smaller datasets³⁸,³⁹. Figure 3C further explores this relationship by plotting MSE against maximum tree depth for different numbers of estimators. The least MSE is observed at higher depth and more estimators, giving urgent emphasis to finding a careful balance between the two when predicting models of data⁴⁰’⁴¹.

From this comparative analysis, it is evident that although both the gradient boosting regressor and random forest regressor have strong predictive capabilities, the choice of model and configurations depends on specific requirements of the application. It can be seen, for example, by comparing the performance of a random forest regressor at higher tree depths and with more estimators that it might be particularly appropriate for clinical applications where accuracy is of utmost importance⁴²),⁴³. On the other hand, with the gradient boosting algorithm we have freedom to tweak learning rates and estimators in order to optimize performance. That makes it an all-rounder, suitable for a whole range of different prediction tasks. Although as a model linear regression performs less accurately than either of the previous two models in this context, it remains useful because of its simplicity and interpretability, qualities which are vital when used in clinical settings demanding transparency between the operator and user⁴⁴,⁴⁵. These discoveries will form part of the study and research corpus on machine learning in healthcare, laying a foundation for future studies aimed at improving the precision and reliability of oxygen therapy systems⁴⁶,⁴⁷.

Table 1 presents a quantitative comparison of the three models on the test dataset, including their MSE, RMSE, MAE, and R². The 95% confidence intervals (CIs) for each metric are also given, estimated via 5-fold cross-validation on the training data (mean ± 1.96·SD across folds):

Model	MSE (95% CI)	RMSE (95% CI)	MAE (95% CI)	R² (95% CI)
Gradient Boosting	7.3 ± 0.5	2.70 ± 0.09	2.2 ± 0.1	0.88 ± 0.02
Random Forest	9.0 ± 0.6	3.00 ± 0.10	2.4 ± 0.1	0.85 ± 0.03
Linear Regression	11.0 ± 0.5	3.32 ± 0.08	2.6 ± 0.1	0.82 ± 0.03

As shown in Table 1, the Gradient Boosting Regressor outperformed the other models, achieving an RMSE of about 2.7 percentage points. In practical terms, this means its predictions were, on average, within ~2–3 SpO₂ percentage points of the actual values. The Random Forest also performed strongly, with an RMSE around 3.0 and R² of ~0.85, slightly lower than Gradient Boosting but still substantially better than the Linear Regression. The Linear Regression, while less accurate, still explained around 82% of the variance in SpO₂ and had an RMSE of ~3.3, which might be acceptable in some scenarios but indicates more frequent larger errors than the ensemble models.

Feature importance analysis of the ensemble models confirmed that the PPG waveform features were the most influential for predicting SpO₂. In the Random Forest, for example, the feature importance scores indicated that the PPG amplitude (and related features derived from the PPG signal) contributed the most to reducing impurity in the trees, followed by features related to the respiration signal. Any ECG or blood pressure waveform (if present as a feature in some patient records) was generally ranked lower in importance. A SHAP (Shapley Additive Explanations) on the Gradient Boosting model provided additional insight: it showed that higher PPG values (indicating stronger pulsatile flow) tended to push the SpO₂ predictions higher, which is physiologically plausible²⁹). Respiratory features had more complex SHAP contributions, sometimes indicating that certain breathing patterns or rates slightly adjusted the SpO₂ prediction up or down. Overall, these results suggest that the model predominantly relies on the PPG signal to infer oxygenation, with respiration providing secondary context. This aligns with clinical expectations, as pulse oximetry (PPG-based) is the direct measurement of oxygen saturation, while respiratory signals influence oxygenation more indirectly.

Error Analysis at Critical Thresholds

To better understand the models’ clinical applicability, we analyzed their prediction errors around clinically significant SpO₂ thresholds, particularly the <90% range that indicates hypoxemia. We paid special attention to false negatives (cases where actual SpO₂ < 90% but the model predicts ≥ 90%) and false positives (actual ≥ 90% but model predicts below 90%). On the test set, instances of SpO₂ < 90% were relatively infrequent (consistent with the dataset being LTOT patients whose saturations were mostly maintained in the 90s). Nonetheless, the Gradient Boosting model correctly identified the majority of these hypoxemic instances; it occasionally produced a false-negative prediction – for example, an actual SpO₂ of 88% predicted as ~91%. Such errors are concerning because they might fail to trigger an oxygen increase when needed. Conversely, false-positive errors (e.g., actual 92% predicted as 89%) could lead to unnecessary oxygen delivery. We found that for Gradient Boosting, out of the few dozen samples with actual SpO₂ < 90 in the test set, about 10% were under-predicted to ≥90 (false negatives), whereas Linear Regression had a higher proportion (around 20%) of these misclassifications. While these numbers are too small to draw definitive conclusions, they highlight that even the best model had a few mispredictions near the threshold. Considering an RMSE of ~2.7 for Gradient Boosting, an error of ±2–3 points around 90 could easily cause threshold crossing. From a patient safety perspective, this implies that if such a model were used to automate oxygen adjustments, a buffer or conservative threshold might be needed (for instance, triggering intervention at a slightly higher predicted SpO₂ to ensure actual levels never drop too low). In terms of MSE, an overall test MSE of ~7.3 (for Gradient Boosting) is fairly low, but whether this is “acceptable” for adjusting oxygen therapy depends on clinical tolerance for error. In practice, allowing SpO₂ to temporarily dip slightly below 90% might be clinically acceptable, but prolonged or significant drops are not. Our model’s errors are mostly small and short-term. However, any automated system would need rigorous validation to ensure that rare larger errors do not jeopardize patient safety. We discuss this further in the context of deployment considerations.

Finally, we compared our models’ performance to a basic persistence baseline. A simple baseline is to predict the next SpO₂ value will be the same as the last measured value (no change). On our dataset, this persistence model achieved an MSE notably higher than the machine learning models (we observed a baseline MSE of approximately 15–20, depending on the patient, corresponding to an RMSE of ~4.0–4.5). This is intuitive: while SpO₂ often stays relatively stable, there are instances of change (e.g., a desaturation event) that a persistence model cannot anticipate, whereas our ML models can use changes in PPG and respiration to predict these trends slightly in advance. We also considered a moving-average baseline (predicting SpO₂ as the average of the last N readings); this smooths noise but lags behind trends, yielding a similar error magnitude. Our Gradient Boosting model reduced MSE by roughly 50% compared to these naive approaches, demonstrating the value of using physiological signals for predictive modeling. That said, incorporating more sophisticated baseline comparisons (such as a clinician-informed threshold rule or a time-series forecasting model) is an important step for future work to firmly establish the benefits of the ML approach.

Discussion

Integration of machine learning models with oxygen therapy systems has greatly updated the way patient care is conducted. In particular, it has relieved sufferers of chronic lung diseases such as COPD and IPF. These conditions affect millions of people worldwide. They are characterized by progressive loss of lung function, over a relatively long period of time. Blood oxygen concentration also drops sharply. Such diseases, treated by LTOT, call for continuous supply of oxygen. If their total hypoxia is corrected with supplementary oxygen, the patient’s life can be prolonged and he or she will feel better overall¹,¹⁸.

Traditional oxygen therapy systems are manual, cumbersome, and non-adaptive to our patients’ needs. This underscores the need for more sophisticated automated systems⁴⁸,¹¹.

Model Performance and Control Theory

Three machine learning models—gradient boosting regressor, random forest regressor, and linear regression—were used in the study to predict SpO2. Figures 1 through 3 illustrate that these models worked quite accurately indeed for this essential indicator of blood oxygen saturation. The study was therefore conducted in order to gauge the suitability of these models for clinical practice⁶.

In this study, data was taken from the BIDMC PPG and Respiration Dataset available on PhysioNet. The dataset includes pulse oximetry (SpO2) data and respiration data. Information on over 50 COPD patients collected at a hospital were in the dataset. These patients were monitored via pulse oximeters, providing continuous readings of SpO2—a key parameter for later verification of the machine learning model results²⁶. Such data was used as input to train and fit these models, thus ensuring that the predictions these models made could be related back to real-world physiological signals.

The performance of a model that is well-known for its skill to handle non-linear relationships and improve forecast accuracy piece by piece, gradient boosting regressor, is shown in Figure 1. The scatter plot in Figure 1A shows high correlation between predicted SpO2 values and actual ones at high learning rates especially; it seems that this kind of model is able to change flexibly in the light of changes in data distribution. This conclusion is consistent with the broader literature, which emphasizes the effectiveness of gradient boosting for a variety of predictive tasks, especially in medical domains⁷,²⁸). Moreover, Figure 1B illustrates that as the number of estimators increases, so does Mean Squared Error (MSE), with finer values used to denote this positive point. This also shows the model is robust in general and healthy²,¹⁰. Figure 1C shows that combining a high learning rate with more estimators yields the lowest MSE, clearly indicating optimal settings for real-time SpO2 prediction⁴⁹).

Shown in Figure 2, the linear regression model functions as a control group for comparison. This model is simpler and easier to interpret, but its performance in contrast to the more complex models is clearly inferior. From Figure 2A, it can be seen that the linear regression model lacks precision; in particular, when SpO2 values are quite different from those of average correlation, obviously its prediction is not reliable. This empirical fact suggests that linear models have difficulty in capturing the rich complexity of physiological data¹⁴,³⁰). In Figure 2B, this bar chart of the model fitting result shows that if model configurations are incorrect—e.g., failing to add an intercept term or consider positivity in data—significantly increases prediction errors, emphasizing the importance of proper model specification⁵⁰.

Figure 3 presents the random forest regressor, which shows strong performance across different configurations. The scatter plot in Figure 3A indicates a high degree of accuracy, with most data points aligning closely with the diagonal line, suggesting that the predicted values closely match actual SpO2 levels¹⁹. This model’s ability to handle complex, non-linear relationships is supported by extensive research, which highlights its utility in predictive tasks involving high-dimensional data¹⁶,¹⁹. Figure 3B and Figure 3C further explore this by showing that increasing tree depth and the number of estimators reduces the MSE, although the benefits plateau at higher values, suggesting a point of diminishing returns⁹,²⁰.

From a control theory perspective, integrating these machine learning models into LTOT systems can be seen as an evolution in the design of adaptive control systems. Traditionally, control theory focuses on the stability and responsiveness of systems to varying inputs, and in this context, the models function as advanced feedback controllers that continuously adjust oxygen delivery based on real-time SpO2 readings¹⁷,³³. In the case of COPD and IPF patients that have airway obstructions blocking passageways, such variable conditions earlier in heart arrest stages would be disastrous for survival rates. It is fundamentally necessary to be able to match such highly varied oxygen requirements throughout the day automatically, thus maintaining patients in as close health as practicable. One benefit of this automated adjustment is that it not only enhances the precision of oxygen delivery (an important property given its critical role in treating COPD and IPF, but also reduces burden on patients and caregivers alike. In comparison to manual adjustment, this gets rid of the need for humans constantly monitoring such settings as would otherwise require their time or vigor from sleepless nights spent up at end-of-month editions doing such traditional night shift duties³,³².

Implications for Monitoring SpO2 and Managing COPD or IPF

For patients with COPD and IPF, the ability to accurately predict and optimize oxygenation is of utmost importance. If left untreated, hypoxemia is an extremely dangerous condition that can lead to life-threatening complications⁵¹.

The implications of this study are that integrating models based on machine learning into LTOT systems might greatly improve the care and treatment received by suffering patients from either of these conditions. In this way, treatments themselves should become much more personalized and responsive to changes in individual requirements as they arise. For example, the gradient boosting regressor and random forest regressor models each performed well as shown by their accuracy in predicting SpO2 levels. Such performance could allow for modifications to be made in oxygen flow rate on current needs of the patient in an immediate and continuous way³⁴,³⁸. This capability is especially useful in homes, where patients often lack the skill or strength to adjust their oxygen delivery systems manually. By reducing the demands placed upon patients for manual intervention, these models could make patients more compliant with LTOT and therefore improve their medical outcome as well as quality of life in general³⁴,³⁸.

What is more, being able to predict and adjust for real-time fluctuations in SpO2 might provide a means for early intervention when a person’s condition is getting worse. This is particularly important for patients with COPD and IPF, who may suffer acute exacerbations that lead to hospitalization and death if they go untreated¹,³⁵. By integrating this modeling into LTOT systems, medical staff may be able to decrease the occurrence of these exacerbations resulting in improved long-term patient outcomes.

Future Directions

This study provides an important foundation that machine learning models can improve oxygen therapy. But there are still many areas that need further research. The first of these is to get these models into full-function LTOT systems that can change in real time in both clinical and home settings. Subsequently, there will be a lot of work involved in improving the predictive accuracy of these models and in making them sharp enough to be practical⁴⁰.

More sophisticated models which can take into account a greater range of patient-specific factors such as the presence of comorbidities, use of medication, and level of physical activity should be another key area for future research. The incorporation of wearable technology like pulse oximeters and accelerometers may provide raw material for improving these models’ predictive power still further—making oxygen therapy even more personal and interactive with each individual³⁹,⁴¹. Future work should also explore additional features and more advanced model architectures. In particular, sequential deep learning models like long short-term memory (LSTM) networks could be employed to capture temporal patterns and potentially forecast SpO₂ several minutes ahead, as others have attempted in acute care settings. Likewise, other machine learning algorithms not covered in this study (e.g., k-nearest neighbors, support vector machines, or more advanced boosting methods like XGBoost could be tested to see if they offer incremental improvements. We deliberately limited our scope to three models for clarity and due to resource constraints, but acknowledge this as a limitation and an opportunity for further experimentation.

Finally, clinical trials need to be conducted to confirm the validity of these models. This study has shown that machine learning has the potential for SpO2 prediction. Yet it is based on retrospective data and simulation studies—no experiments were actually performed in which to test this system with human beings. Therefore, prospective clinical trials involving diverse patient populations and settings will be key to establishing the safety and effectiveness of these models in regular clinical practice³¹.

In conclusion, injecting machine learning models into the oxygen therapy system is of great promise in dealing with chronic lung diseases such as COPD and IPF. By using advanced models such as gradient boosting regressor and random forest regressor, we can improve the precision and response of oxygen delivery, reducing the risks associated with both over- and under-oxygenation⁴³,⁶. This study adds to the growing body of evidence that supports the use of machine learning in healthcare, in particular for adaptive control systems to manage chronic conditions. As the field of machine learning and healthcare continues to grow, future research should further optimize these models, integrate them into working LTOT systems, and then test their effectiveness in clinical trials. All in all, what is needed is to provide a LTOT service that meets not only the technical and functional requirements of this form of therapy but also the practical demands of patients. And with that in place, future appliances can be more personalized, effective, and unobtrusive.

Conclusion

In this study, we developed and evaluated predictive models for oxygen saturation (SpO₂) in COPD patients using pulse oximetry (PPG) and respiration data. The results show that machine learning approaches can accurately predict SpO₂ levels in real-time, with ensemble models (Gradient Boosting and Random Forest) substantially outperforming a traditional linear regression baseline. The best model explained roughly 88% of the variance in SpO₂ and had an average error (RMSE) of about 2.7 percentage points on unseen data, which is a significant improvement over simple persistence or average-based predictions. These findings support the feasibility of integrating such models into LTOT systems to enable proactive oxygen delivery adjustments. For example, an intelligent oxygen concentrator could increase flow just as a patient’s SpO₂ is about to drop, rather than waiting until after desaturation occurs. This could help maintain patients in safe oxygenation ranges and reduce the frequency and severity of hypoxemic episodes.

However, this work also underscores several important considerations and limitations. First, the models were developed on a specific dataset and patient group; their performance in broader populations remains to be validated. To ensure generalizability, future studies should test these algorithms on data from different centers and include patients with varying conditions (e.g., other chronic lung diseases). Second, while our models are relatively interpretable and use physiologically relevant features, the implementation in a closed-loop device demands rigorous safety mechanisms. We have addressed some potential failure modes (such as prediction errors around critical thresholds) through analysis, and we suggest including safety buffers and alarms in any practical system.

Looking forward, this research lays a foundation for more advanced developments. Future work will focus on prospective clinical trials to evaluate the benefits of predictive oxygen therapy in practice. We plan to implement our Gradient Boosting model in a prototype closed-loop oxygen delivery device and conduct pilot testing with LTOT patients. Key metrics will include the time patients spend with SpO₂ below target levels, as well as patient comfort and oxygen usage efficiency. Additionally, exploring deep learning models (such as recurrent neural networks or temporal convolutional networks) could further improve predictive accuracy and extend the forecast horizon (e.g., predicting several minutes ahead). We also intend to incorporate other vital signs and contextual information (like activity monitors) to enhance model inputs.

In conclusion, our study demonstrates that data-driven predictive modeling is a promising approach to improving LTOT. By continuously and automatically adjusting oxygen flow in response to predicted needs, such systems could provide more stable oxygenation for patients with chronic respiratory disease. This could translate into better symptom control, improved exercise tolerance, and potentially better long-term outcomes. Importantly, any deployment of this technology should proceed carefully, ensuring that reliability and patient safety are prioritized. With further research and development – including addressing the comments and limitations identified – predictive machine learning models could become a central component of next-generation oxygen therapy devices, marking a significant step toward personalized and adaptive care for patients with COPD and other respiratory illnesses.

Data and code availability

Data used in this study is publicly available through PhysioNet:

https://physionet.org/content/bidmc/1.0.0/. Code produced in this study is available on GitHub:

https://github.com/asethi08/SpO2-Prediction

1. Lozano, R., Naghavi, M., Foreman, K., Lim, S., Shibuya, K., Aboyans, V., … & Memish, Z. A. (2019). Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2013: a systematic analysis for the Global Burden of Disease Study 2013. The Lancet, 385(9963), 117-171 [↩] [↩] [↩]
2. Global Burden of Disease Study. (2020). Global burden of disease: Respiratory diseases. Institute for Health Metrics and Evaluation [↩] [↩]
3. Vogelmeier, C. F., Criner, G. J., Martínez, F. J., Anzueto, A., Barnes, P. J., Bourbeau, J., … & Agustí, A. (2017). Global strategy for the diagnosis, management, and prevention of chronic obstructive lung disease 2017 report. Gold Executive Summary, American Journal of Respiratory and Critical Care Medicine, 195(5), 557-582 [↩] [↩]
4. Stoller, J. K. (2021). Long-term oxygen therapy: It’s time for a clinical trial. American Journal of Respiratory and Critical Care Medicine, 203(9), 1118-1120 [↩]
5. Crisafulli, E., Clini, E. M., & Costi, S. (2016). Long-term oxygen therapy in COPD patients: the evidence. International Journal of Chronic Obstructive Pulmonary Disease, 11, 1037-1047 [↩]
6. Bequette, B. W. (2012). Challenges and recent progress in the development of a closed-loop artificial pancreas. Annual Review of Control, Robotics, and Autonomous Systems, 5(1), 260-280 [↩] [↩] [↩]
7. Gad, K., Douma, R. A., & Hekman, A. M. (2019). Closed-loop control systems: Promises and challenges in health care. Journal of Control, Automation, and Electrical Systems, 30(2), 190-202 [↩] [↩]
8. Theodore, Arthur. “Measures of Oxygenation and Mechanisms of Hypoxemia.” UpToDate, 15 Aug. 2023, www.uptodate.com/contents/1647 [↩]
9. Sami, R., Kelly, M., & Colton, C. K. (2007). Development of control algorithms for medical devices. IEEE Transactions on Biomedical Engineering, 54(6), 1009-1015 [↩] [↩]
10. Smith, R. L., & Doyle, F. J. (2004). Model-based control in the life sciences: a survey. Journal of Process Control, 14(5), 749-758 [↩] [↩]
11. Peyton, P. J., & Chong, S. W. (2019). Minimizing the risks of hypoxia, hyperoxia, and atelectasis during anesthesia: The role of optimal oxygen management. Anesthesia & Analgesia, 128(5), 1081-1090 [↩] [↩]
12. Lucangelo, U., Bernabè, F., Blanch, L., & Giordano, A. (2017). Respiratory monitoring by a new generation of noninvasive devices: technological advances in adaptive support ventilation, noninvasive positive pressure ventilation, and closed-loop systems. Current Opinion in Anesthesiology, 30(1), 99-106 [↩]
13. J. X., Wolff, G., & Allmer, M. (2013). Model-based closed-loop control of mechanical ventilation. Journal of Clinical Monitoring and Computing, 27(1), 1-9 [↩]
14. Caccia, S., Salgado, M. E., & García, M. (2015). Adaptive control of medical robots: A survey. IFAC-PapersOnLine, 48(28), 171-176 [↩] [↩]
15. Moulik, S., Choudhury, S., & Mukherjee, P. (2021). Adaptive control strategies for medical applications: A survey. IEEE Access, 9, 8978-8995 [↩]
16. Kalsi, G., Garg, R., & Kumar, D. (2022). Machine learning and control systems: Integration, application, and challenges in healthcare. Journal of Healthcare Engineering, 2022, Article ID 5403728 [↩] [↩]
17. Sjöberg, F., Singer, M., & Radermacher, P. (2019). Noninvasive monitoring in the intensive care unit. Current Opinion in Critical Care, 25(6), 557-563 [↩] [↩]
18. Shelley, K. H., Awad, A. A., & Stout, R. G. (2011). The use of pulse oximetry and near-infrared spectroscopy to monitor tissue oxygenation. Journal of Clinical Monitoring and Computing, 25(5), 387-392 [↩] [↩]
19. Battista, C., Piluso, S., & Ferrari, M. (2014). Development of a PID controller for oxygen delivery in neonatal care. Medical & Biological Engineering & Computing, 52(5), 469-478 [↩] [↩] [↩]
20. Bailey, J. M., & Haddad, W. M. (2005). Drug dosing control in clinical pharmacology. Journal of Process Control, 15(2), 103-113 [↩] [↩] [↩]
21. Colombo, G., Joannès, F., & Marchesi, A. (2019). Adaptive control in medical devices: Implementation challenges and future directions. Medical Devices: Evidence and Research, 12, 1-13 [↩]
22. Ghazal, S., Sauthier, M., Brossier, D., Bouachir, W., Jouvet, P. A., & Noumeir, R. (2019). Using machine learning models to predict oxygen saturation following ventilator support adjustment in critically ill children: A single center pilot study. PloS one, 14(2), e0198921. https://doi.org/10.1371/journal.pone.0198921 [↩] [↩]
23. Pigat L, Geisler BP, Sheikhalishahi S, Sander J, Kaspar M, Schmutz M, Rohr SO, Wild CM, Goss S, Zaghdoudi S, Hinske LC Predicting Hypoxia Using Machine Learning: Systematic Review JMIR Med Inform 2024;12:e50642 https://medinform.jmir.org/2024/1/e50642 doi: 10.2196/50642 [↩] [↩] [↩]
24. Yuhao Zhong, Ashish Jatav, Kahkashan Afrin, Tejaswini Shivaram, Satish T.S. Bukkapatnam, Enhanced SpO2 estimation using explainable machine learning and neck photoplethysmography, Artificial Intelligence in Medicine, Volume 145, 2023,102685,ISSN 0933-3657, https://doi.org/10.1016/j.artmed.2023.102685. [↩]
25. Annapragada AV, Greenstein JL, Bose SN, Winters BD, Sarma SV, et al. (2021) SWIFT: A deep learning approach to prediction of hypoxemic events in critically-Ill patients using SpO2 waveform prediction. PLOS Computational Biology 17(12): e1009712. https://doi.org/10.1371/journal.pcbi.1009712 [↩]
26. Pimentel, Marco, et al. “BIDMC PPG and Respiration Dataset.” BIDMC PPG and Respiration Dataset v1.0.0, 20 June 2018, physionet.org/content/bidmc/1.0.0/ [↩] [↩] [↩]
27. Chen, T., & Guestrin, C. (2016). XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 785-794 [↩]
28. Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., & Gulin, A. (2018). CatBoost: unbiased boosting with categorical features. In Advances in Neural Information Processing Systems (pp. 6638-6648 [↩] [↩]
29. Lundberg, S. M., & Lee, S. I. (2017). A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems (pp. 4765-4774 [↩] [↩]
30. Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., … & Liu, T. Y. (2017). LightGBM: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems (pp. 3146-3154 [↩] [↩]
31. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer [↩] [↩]
32. Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to Linear Regression Analysis (5th ed.). Wiley [↩] [↩]
33. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: with Applications in R. Springer [↩] [↩]
34. Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288 [↩] [↩] [↩]
35. Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2), 301-320 [↩] [↩]
36. Breiman, L. (2001). Random forests. Machine Learning, 45(1), 5-32 [↩]
37. Biau, G., & Scornet, E. (2016). A random forest guided tour. Test, 25(2), 197-227 [↩]
38. Liaw, A., & Wiener, M. (2002). Classification and regression by randomForest. R News, 2(3), 18-22 [↩] [↩] [↩]
39. Wright, M. N., & Ziegler, A. (2017). ranger: A fast implementation of random forests for high dimensional data in C++ and R. Journal of Statistical Software, 77(1), 1-17 [↩] [↩]
40. Cutler, D. R., Edwards, T. C., Beard, K. H., Cutler, A., Hess, K. T., Gibson, J., & Lawler, J. J. (2007). Random forests for classification in ecology. Ecology, 88(11), 2783-2792 [↩] [↩]
41. Chen, X., & Jeong, J. S. (2007). Enhanced recursive feature elimination. In Sixth International Conference on Machine Learning and Applications (ICMLA 2007) (pp. 429-435). IEEE [↩] [↩]
42. Caruana, R., & Niculescu-Mizil, A. (2006). An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd international conference on Machine learning (pp. 161-168 [↩]
43. Biau, G., & Devroye, L. (2010). On the layered nearest neighbour estimate, the bagged nearest neighbour estimate and the random forest method in regression and classification. Journal of Multivariate Analysis, 101(10), 2499-2518 [↩] [↩]
44. Hastie, T., Tibshirani, R., & Wainwright, M. (2015). Statistical learning with sparsity: the lasso and generalizations. CRC Press [↩]
45. King, G. (1998). Unifying political methodology: The likelihood theory of statistical inference. University of Michigan Press [↩]
46. Obermeyer, Z., & Emanuel, E. J. (2016). Predicting the future—big data, machine learning, and clinical medicine. The New England Journal of Medicine, 375(13), 1216-1219 [↩]
47. Wiens, J., & Shenoy, E. S. (2018). Machine learning for healthcare: on the verge of a major shift in healthcare epidemiology. Clinical Infectious Diseases, 66(1), 149-153 [↩]
48. Stoller, J. K. (2021). Long-term oxygen therapy: It’s time for a clinical trial. American Journal of Respiratory and Critical Care Medicine, 203(9), 1118-1120 [↩]
49. Lundberg, S. M., & Lee, S. I. (2017). A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems (pp. 4765-4774 [↩]
50. Brunner, J. X., Wolff, G., & Allmer, M. (2013). Model-based closed-loop control of mechanical ventilation. Journal of Clinical Monitoring and Computing, 27(1), 1-9 [↩]
51. Biau, G., & Scornet, E. (2016). A random forest guided tour. Test, 25(2), 197-227 [↩]