Abstract
Delay discounting is defined as the tendency to devalue rewards as their delay increases, and it is a fundamental component of decision-making that enables cognitive scientists to investigate human behavior. In this study, we investigate whether augmenting classic-value based models with a response-bias parameter (![]() ) improves descriptive adequacy or aligns with independent inhibitory control. We combined simulations and participant fits across three models: 1) hyperbolic, 2) hyperboloid, 3) dual-variant that adds (
) improves descriptive adequacy or aligns with independent inhibitory control. We combined simulations and participant fits across three models: 1) hyperbolic, 2) hyperboloid, 3) dual-variant that adds (![]() ) to choice rule. Simulations over a
) to choice rule. Simulations over a ![]() on the Monetary Choice Questionnaire (MCQ) by Kirby et al. with canonical parameters (
on the Monetary Choice Questionnaire (MCQ) by Kirby et al. with canonical parameters (![]() ,
, ![]() ) showed that delayed choices concentrate only when both the discount rate
) showed that delayed choices concentrate only when both the discount rate ![]() and
and ![]() are low; increasing alpha shifts choices toward the immediate option, which is consistent with immediate gains. In participant data, hyperbolic discounting provided the best Akaike information criterion (AIC) for every converged case (
are low; increasing alpha shifts choices toward the immediate option, which is consistent with immediate gains. In participant data, hyperbolic discounting provided the best Akaike information criterion (AIC) for every converged case (![]() ). The dual model fit worse (median
). The dual model fit worse (median ![]() ;
; ![]() ) and exhibited boundary solutions (
) and exhibited boundary solutions (![]() at the lower bound in 93.4%;
at the lower bound in 93.4%; ![]() at the upper bound in 51.3%). Fitted
at the upper bound in 51.3%). Fitted ![]() correlated negatively with the proportion of delayed choices (
correlated negatively with the proportion of delayed choices (![]() ,
, ![]() ) and showed no reliable associated with stop-signal reaction time (SSRT;
) and showed no reliable associated with stop-signal reaction time (SSRT; ![]() ,
, ![]() ). First-order Sobol indices were small for all parameters. These results indicate that a single decision-stage gain neither improves model fit nor tracks inhibitory control in these data; instead, alpha acts as an immediacy bias, while simple hyperbolic valuation remains sufficient for standard intertemporal-choice tasks.
). First-order Sobol indices were small for all parameters. These results indicate that a single decision-stage gain neither improves model fit nor tracks inhibitory control in these data; instead, alpha acts as an immediacy bias, while simple hyperbolic valuation remains sufficient for standard intertemporal-choice tasks.
Introduction
Delay discounting refers to the systematic decline in the subjective value of a reward as the delay to its receipt increases. It is a foundational concept in behavioral economics and cognitive neuroscience, widely used to model impulsive decision-making1,2,3,4. In delay discounting tasks, agents choose between a smaller immediate reward and a larger delayed one. Choosing the immediate option is interpreted as a more impulsive or short-sighted decision. This paradigm has become a gold standard for quantifying individual differences in impulsivity and self-control.
Impulsive discounting behavior has strong predictive power in clinical and everyday contexts. Steeper discounting (valuing future rewards significantly less than immediate ones) has been robustly linked to a range of maladaptive outcomes. For instance, individuals with substance use disorders, gambling addiction, and obesity typically show higher delay discounting rates compared to healthy controls5,6,7,8,9. These individuals tend to prefer short-term gratification (i.e., a drug high or snack) despite long-term costs (i.e., health, financial stability). Steeper discounting is also predictive of earlier relapse in addiction treatment and poorer treatment adherence10,11. Given its clinical and theoretical relevance, delay discounting has emerged as a key behavioral marker of impulsivity across populations.
However, impulsivity is a multifaceted construct. Temporal discounting captures one dimension, but executive function and inhibitory control play additional roles in regulating decision-making. The ability to inhibit prepotent or reflexive responses (motor impulsivity) is a distinct but related trait. Importantly, empirical studies show that individuals with weaker inhibitory control often exhibit steeper delay discounting12,13. For example, adolescents with attention-deficit/hyperactivity disorder (ADHD) who perform poorly on response inhibition tasks also tend to favor immediate over delayed rewards more often14,15. These findings suggest that the ability to value delayed rewards is not solely a function of subjective valuation, but also of self-regulatory capacity. Some theorists have argued that temporal discounting itself should be considered part of the broader executive function system12,16.
This study addresses that gap by augmenting classical value-based discounting with an explicit response-bias parameter, α, embedded in the choice rule17. Conceptually, k governs how sharply delayed rewards are devalued, whereas α scales the effective weight of the immediate option at decision time. In simulations, we use a deterministic threshold rule to cleanly map how k and α jointly shape choice patterns over a standard set of intertemporal offers. For empirical data we couple valuation with a logistic choice rule that includes a temperature parameter τ; this allows us to fit individual participants’ choices by maximum likelihood and to compare competing models with Akaike’s information criteria (AIC). We further evaluate the construct validity of α by testing whether it aligns with (i) observed choice behavior (proportion of delayed choices) and (ii) an independent inhibitory-control measure, stop-signal reaction time (SSRT)18,19,20.
Methodologically, the approach is two-pronged. First, we perform large-scale simulations on the canonical Monetary Choice Questionnaire (MCQ) by Kirby et al. to produce a k×α landscape of delayed-choice behavior under a fixed noise/temperature setting21. We also run a global sensitivity analysis (first-order Sobol indices) to quantify the marginal influence of each parameter on delayed-choice probability across the grid. Second, we fit three models to individual participants: (i) hyperbolic (Mazur)17, (ii) hyperboloid (Myerson–Green)17,22, and (iii) a dual variant that adds α to the choice rule. We conduct model selection by AIC, examine parameter distributions and correlations, and assess whether fitted α tracks either behavior or SSRT19,20,18.
Lines of previous work explain intertemporal choice with valuation alone (e.g., hyperbolic/hyperboloid)17,23, but dual-process perspectives argue for separable influences of valuation and control (e.g., “hot–cool” or competing-systems accounts)24,25,26,27. Motivated by these views, we formalized α as a decision-stage immediacy gain: at choice time, the immediate option is effectively up-weighted, shifting selections toward smaller–sooner outcomes as α increases. This operationalization complements classic valuation by isolating response bias from subjective value. Our formulation is further expanded upon in the Methods section.
Our specific objectives are as follows: (1) formalize an explicit, decision-stage response-bias parameter α within standard discounting frameworks17; (2) map the joint effects of discount rate k and response bias α on intertemporal choice via grid-based simulations on a widely used trial set (MCQ)21; (3) fit hyperbolic, hyperboloid, and dual models to participant data and compare them using AIC, including checks for parameter identifiability and boundary solutions17,22; (4) evaluate the behavioral and external validity of α by correlating it with the proportion of delayed choices and with SSRT19,20,18; and (5) quantify the marginal contribution of each parameter to delayed-choice behavior using Sobol sensitivity analysis. This design enables a direct test of whether adding a control-like gain improves descriptive adequacy beyond value-only models and clarifies what aspect of behavior the α term actually captures.
Results
We report simulation results that sweep the discount rate ![]() and the response-bias gain
and the response-bias gain ![]() on the Kirby trial set, together with empirical model fits to participant data. Unless noted, the canonical simulation setting uses
on the Kirby trial set, together with empirical model fits to participant data. Unless noted, the canonical simulation setting uses ![]() and stimulus noise
and stimulus noise ![]() . Across the
. Across the ![]() grid, delayed-choice behavior was high only when both
grid, delayed-choice behavior was high only when both ![]() and
and ![]() were low (Fig. 1). Increasing either parameter drove agents toward immediate choices, and increasing
were low (Fig. 1). Increasing either parameter drove agents toward immediate choices, and increasing ![]() in particular reduced the proportion of delayed choices to near zero over much of the grid. In this implementation,
in particular reduced the proportion of delayed choices to near zero over much of the grid. In this implementation, ![]() therefore functions as an urgency or immediacy gain rather than a patience-promoting control, concentrating delayed responding in the low-
therefore functions as an urgency or immediacy gain rather than a patience-promoting control, concentrating delayed responding in the low-![]() , low-
, low-![]() corner. The qualitative patterns was unchanged across
corner. The qualitative patterns was unchanged across ![]() and
and ![]() (Supplementary Figures S1–S3).
(Supplementary Figures S1–S3).



 grid (canonical
grid (canonical  ,
, 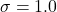 ). Delayed responding is concentrated in the low-
). Delayed responding is concentrated in the low- , low-
, low- corner; elsewhere delayed choice is near zero.
corner; elsewhere delayed choice is near zero.In the participant fits, hyperbolic discounting was preferred by AIC for every individual with converged estimates (![]() ; Fig. 2). The dual model that augments the choice rule performed worse than both comparators: median
; Fig. 2). The dual model that augments the choice rule performed worse than both comparators: median ![]() and
and ![]() . Only 7.9% (dual-hyperbolic) and 9.2% (dual-hyperboloid) of cases showed negative
. Only 7.9% (dual-hyperbolic) and 9.2% (dual-hyperboloid) of cases showed negative ![]() AIC, aligning with the overall log-likelihood distributions and indicating that adding a decision-stage gain did not improve descriptive adequacy for these data.
AIC, aligning with the overall log-likelihood distributions and indicating that adding a decision-stage gain did not improve descriptive adequacy for these data.


 vs. hyperbolic;
vs. hyperbolic;  vs. hyperboloid.
vs. hyperboloid.Parameter behavior within the dual model showed pronounced boundary solutions (Fig. 3, 4). Specifically, ![]() piled at its lower bound for 71/76 (93.4%) participants,
piled at its lower bound for 71/76 (93.4%) participants, ![]() hit the upper bound (
hit the upper bound (![]() ) for 39/76 (51.3%), and
) for 39/76 (51.3%), and ![]() took its minimum value for 72/76 (94.7%). The
took its minimum value for 72/76 (94.7%). The ![]() —
—![]() correlation was positive (Pearson
correlation was positive (Pearson ![]() , 95% CI [0.171, 0.559]), whereas correlations of
, 95% CI [0.171, 0.559]), whereas correlations of ![]() with
with ![]() or
or ![]() were near zero (CIs include 0). Together with the AIC results, this pattern indicates weak identifiability of the added control terms given the present task and data.
were near zero (CIs include 0). Together with the AIC results, this pattern indicates weak identifiability of the added control terms given the present task and data.



 and
and  (near zero).
(near zero).We next asked whether ![]() relates to observed behavior and to an independent inhibitory-control measure. Across the AIC sample,
relates to observed behavior and to an independent inhibitory-control measure. Across the AIC sample, ![]() correlated negatively with the proportion of delayed choices (Pearson
correlated negatively with the proportion of delayed choices (Pearson ![]() , 95% CI [
, 95% CI [![]() ,
, ![]() ],
], ![]() ; Fig. 5). In an independent cohort with stop-signal reaction time (SSRT;
; Fig. 5). In an independent cohort with stop-signal reaction time (SSRT; ![]() ),
), ![]() showed no reliable association with SSRT (Pearson
showed no reliable association with SSRT (Pearson ![]() , 95% CI [
, 95% CI [![]() ,
, ![]() ],
], ![]() ; Fig. 5). These results caution against interpreting
; Fig. 5). These results caution against interpreting ![]() as a trait-like inhibitory-control parameter without external validation.
as a trait-like inhibitory-control parameter without external validation.


 . Larger
. Larger  predicts fewer delayed choices and shows no association with SSRT.
predicts fewer delayed choices and shows no association with SSRT.Finally, first-order Sobol indices (![]() ) computed on the Kirby trial set were small for all parameters (
) computed on the Kirby trial set were small for all parameters (![]() ,
, ![]() ,
, ![]() ; Fig. 6). This sensitivity profile indicates weak marginal influence of any single parameter on delayed-choice probability when averaged across the grid and is consistent with the empirical boundary solutions and with the AIC preference for the simpler hyperbolic model (see also Supplementary Figures S4–S5 for alternative sensitivity visualizations). Together, the simulations and fits converge on the same conclusion: variation in
; Fig. 6). This sensitivity profile indicates weak marginal influence of any single parameter on delayed-choice probability when averaged across the grid and is consistent with the empirical boundary solutions and with the AIC preference for the simpler hyperbolic model (see also Supplementary Figures S4–S5 for alternative sensitivity visualizations). Together, the simulations and fits converge on the same conclusion: variation in ![]() explains the data well, whereas adding the dual-control terms (
explains the data well, whereas adding the dual-control terms (![]() ,
, ![]() ) does not improve descriptive adequacy; moreover,
) does not improve descriptive adequacy; moreover, ![]() behaves as an immediate-choice bias rather than a validated inhibitory control proxy in this context.
behaves as an immediate-choice bias rather than a validated inhibitory control proxy in this context.

 ) for
) for  ,
,  , and
, and  on the Kirby trial set. Bars are small for all parameters.
on the Kirby trial set. Bars are small for all parameters.Discussion
Our study presents a computational framework that integrates valuation and executive control in delay discounting behavior24,25,23. The key findings demonstrate that (1) higher discount rates k lead to more impulsive, immediate-reward choices and lower total earnings17,23; (2) we originally hypothesized that higher inhibitory control α would promote patient decision-making, but in the present implementation, α behaved as an immediacy/response-bias gain; (3) the hyperbolic model, not the hyperboloid, provided the best descriptive fit for all particiants with converged estimates, with the dual model that augments the choice rule with α fitting worse by AIC17,22; and (4) agents showed a robust magnitude effect, choosing delayed rewards more frequently when the rewards were larger23. In addition, dual-model parameters frequently hit bounds (α at its lower bound for 93.4% of participants, τ at its upper bound for 51.3%, and k at its minimum for 94.7%), and first-order Sobol indices were small across parameters, indicating limited marginal influence when averaged over the grid.
These findings are significant for several reasons. First, they support the empirical literature suggesting that impulsive choice is not solely driven by reward valuation but also moderated by decision-stage factors24,25,26,27. However, the absence of an associated between α and an independent inhibitory control measure (SSRT; r=0.07,p=0.49) cautions against interpreting α as a traitlike inhibitory-control construct without external validation28,29,30. Our simulations reinforce that steep delay discounting can stem from two sources: a high discount rate or a response-bias/urgency tendency at choice26,27. Second, this dual-source account helps clarify why individuals with similar k values may behave differently under uncertainty: differences in immediacy bias (α) can tilt decisions toward smaller-sooner options even when value differences are modest. Third, our modeling advances traditional delay discounting frameworks by explicitly integrating a decision-stage term, showing that a one-parameter value function (hyperbolic) often suffices once a reasonable stochastic choice rule is in place, and that adding a control gain can introduce identifiability challenges when the task afford limited leverage to separate valuation from response bias17,22.
In relation to our objectives, all four goals were successfully met. We implemented and compared three major discounting models, systematically varied ![]() and
and ![]() , and captured known behavioral effects. Empirically, the hyperbolic model outperformed both the hyperboloid and dual-models by AIC; the dual model exhibited boundary solutions and weak identifiability;
, and captured known behavioral effects. Empirically, the hyperbolic model outperformed both the hyperboloid and dual-models by AIC; the dual model exhibited boundary solutions and weak identifiability; ![]() related to delayed-choice behavior but not to SSRT; and global sensitivity analysis (first-order Sobol indices) indicated limited marginal influence of individual parameters when averaged across the
related to delayed-choice behavior but not to SSRT; and global sensitivity analysis (first-order Sobol indices) indicated limited marginal influence of individual parameters when averaged across the ![]() grid. Simulations mirrored the empirical patterns: delayed responses were concentrated in the low-
grid. Simulations mirrored the empirical patterns: delayed responses were concentrated in the low-![]() , low-
, low-![]() region under the primary setting
region under the primary setting ![]() ,
, ![]() .
.
Limitations of this work include the notion that agents do not iteratively learn from feedback or update their strategies, meaning that the current framework may not be as dynamic as human decision-making is31,32. In addition, while the deterministic nature of the virtual agents makes it ideal for understanding the discounting model behaviors, it is unlike a real-world scenario where noisy disruptions of behavior are typically observed. Our use of fixed-frame monetary choices (Kirby MCQ) offers limited leverage to dissociate valuation from response bias, which likely contributed to boundary solutions and small Sobol indices33. We also did not include out-of-sample predictive tests due to modest trial counts, nor did we benchmark against learning-based agents given the static nature of the MCQ31,32. Finally, α’s lack of association with SSRT in our dataset argues against treating it as a trait-level inhibitory control measure without external validation28,29,30. Together, these limitations bound our claims to the present task and implementation.
Our results indicate that α functions as an immediacy/urgency gain rather than a traitlike inhibitory-control parameter, and that orthogonal manipulations of immediacy should increase power to identify it and enable contrasts with inhibition-focused measures28,26,27. This simulation-fit-validation pipeline clarifies that the control-like term adds value not by improving fit here or serving as a proxy for inhibitory control, but as a manipulable response-bias knob whose behavioral signature is separable from valuation under appropriately designed conditions. Future work should look to extend this framework with reinforcement-learning and attention models31,32.
Methods
We evaluated three valuation rules for delayed rewards that vary in how they map delay ![]() to subjective value
to subjective value ![]() . The hyperbolic (Mazur) rule is
. The hyperbolic (Mazur) rule is
(1) ![]()
with discount rate ![]() \cite{2}. The hyperboloid (Myerson–Green) generalizes this with a curvature parameter
\cite{2}. The hyperboloid (Myerson–Green) generalizes this with a curvature parameter ![]() :
:
(2) ![]()
We also considered a dual variant that retains hyperbolic valuation but augments the decision stage with a response-bias parameter ![]() (defined below). Intuitively,
(defined below). Intuitively, ![]() controls the steepness of temporal devaluation,
controls the steepness of temporal devaluation, ![]() controls the curvature of the discount function, and
controls the curvature of the discount function, and ![]() controls the effective weight placed on the immediate option at choice time.
controls the effective weight placed on the immediate option at choice time.
For simulations, choices were deterministic to isolate model mechanics: the agent chose the delayed option if and only if:
(3) ![]()
where ![]() denotes the immediate amount. In this formulation, a larger
denotes the immediate amount. In this formulation, a larger ![]() makes immediate choices more likely (an urgency/response-bias gain). For empirical fits to participant data, we used a probabilistic choice rule with temperature
makes immediate choices more likely (an urgency/response-bias gain). For empirical fits to participant data, we used a probabilistic choice rule with temperature ![]() ,
,
(4) ![]()
so that larger ![]() yields noisier choices. All parameters were constrained to positive ranges with broad upper bounds during optimization.
yields noisier choices. All parameters were constrained to positive ranges with broad upper bounds during optimization.
We considered alternative control parameterizations, including an additive decision threshold ![]() on the value difference,
on the value difference,
(5) ![]()
At fixed immediate amounts ![]() , the multiplicative form of
, the multiplicative form of ![]() and the additive
and the additive ![]() are linearly related (
are linearly related (![]() ). We adopt the multiplicative form to (i) keep the bias expressed in units of the immediate stake, which scales naturally with trial magnitude; (ii) avoid introducing a free bias that can drift independently of task stakes; and (iii) make the implied threshold transparent in the deterministic limit used for simulations. With limited leverage to dissociate valuation and bias, these forms can be weakly identifiable.
). We adopt the multiplicative form to (i) keep the bias expressed in units of the immediate stake, which scales naturally with trial magnitude; (ii) avoid introducing a free bias that can drift independently of task stakes; and (iii) make the implied threshold transparent in the deterministic limit used for simulations. With limited leverage to dissociate valuation and bias, these forms can be weakly identifiable.
Our primary criterion is AIC (![]() ) as reported in the main text. Simulations and sensitivity analyses used the canonical 27-item Kirby Monetary Choice Questionnaire (MCQ) trial set to define the immediate/delayed offers. We generated heatmaps by sweeping a log-spaced grid over the parameter ranges
) as reported in the main text. Simulations and sensitivity analyses used the canonical 27-item Kirby Monetary Choice Questionnaire (MCQ) trial set to define the immediate/delayed offers. We generated heatmaps by sweeping a log-spaced grid over the parameter ranges
(6) ![]()
and computed the proportion of delayed choices at each grid point. Unless otherwise noted, the canonical setting fixed the choice temperature at ![]() and stimulus noise at
and stimulus noise at ![]() ; additional settings
; additional settings ![]() and
and ![]() are reported in the Supplement.
are reported in the Supplement.
For participant analyses, we fit the hyperbolic, hyperboloid, and dual models to individual choice data and compared them using AIC. Parameters were estimated by bounded maximum likelihood (minimizing negative log-likelihood under the logistic rule). For a model ![]() with
with ![]() free parameters and maximum log-likelihood
free parameters and maximum log-likelihood ![]() , we computed AIC.
, we computed AIC.
Degrees of freedom corresponded to the parameters estimated under the logistic choice rule: hyperbolic (![]() ,
, ![]() ) has
) has ![]() ; hyperboloid (
; hyperboloid (![]() ,
, ![]() ,
, ![]() ) has
) has ![]() ; dual-model (
; dual-model (![]() ,
, ![]() ,
, ![]() ) has
) has ![]() . We identified the lowest-AIC model per participant and summarized participant-wise
. We identified the lowest-AIC model per participant and summarized participant-wise ![]() AIC. The converged sample comprised
AIC. The converged sample comprised ![]() participants. To assess external validity, we analyzed stop-signal reaction time (SSRT) in an independent cohort from OpenNeuro dataset ds004636 (“Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation”)29,34. SSRT was computed with a standard integration method following consensus recommendations28.
participants. To assess external validity, we analyzed stop-signal reaction time (SSRT) in an independent cohort from OpenNeuro dataset ds004636 (“Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation”)29,34. SSRT was computed with a standard integration method following consensus recommendations28.
We quantified the marginal influence of parameters on delayed-choice probability using first-order Sobol indices (S1), evaluated over the same parameter ranges as the heatmaps on the Kirby trial set. This provides a global sensitivity summary of how variation in each parameter, considered independently, contributes to the variance in the delayed-choice outcome; extended sensitivity summaries are provided in the Supplement.
To relate the fitted control-like parameter to behavior and to an independent measure of inhibition, we correlated ![]() with (i) the observed proportion of delayed choices in the AIC sample (
with (i) the observed proportion of delayed choices in the AIC sample (![]() ) and (ii) SSRT in the independent cohort (
) and (ii) SSRT in the independent cohort (![]() )28,29,30. We report Pearson and Spearman coefficients for robustness.
)28,29,30. We report Pearson and Spearman coefficients for robustness.
All analyses were conducted in Python (NumPy, pandas, SciPy, SALib for Sobol indices, and Matplotlib/Seaborn for figures). AIC was derived from negative log-likelihoods. Simulations used deterministic choice rules (no learning), so results are seed-invariant; any stochastic resample uses a fixed NumPy seed in code.
Supplementary Material



 —
— heatmaps for
heatmaps for  . Proportion of delayed choices across three stimulus-noise settings.
. Proportion of delayed choices across three stimulus-noise settings.

 —
— heatmaps for
heatmaps for  . Panels complement the main-text condition (
. Panels complement the main-text condition (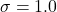 )
)


 —
— heatmaps for
heatmaps for  . Proportion of delayed choices across three stimulus-noise settings.
. Proportion of delayed choices across three stimulus-noise settings.

| Model | N | Percent |
| hyperbolic | 76 | 100.0% |
| hyperboloid | 0 | 0.0% |
| dual | 0 | 0.0% |
| Comparison | Mean | Median | % (< 0) | Note |
| dual → hyperbolic | +17.55 | +11.63 | 7.9% | Positive = dual fits worse |
| dual → hyperboloid | +15.13 | +9.70 | 9.2% | Positive = dual fits worse |
| PID | ||||||||
| K0000 | 24.42 | 26.33 | 48.13 | 23.72 | 21.80 | 0.00 | 0.01 | 10.00 |
| K0001 | 30.65 | 32.63 | 49.13 | 18.48 | 16.50 | 0.00 | 0.01 | 10.00 |
| K0002 | 59.08 | 60.70 | 96.05 | 36.97 | 35.36 | 0.00 | 0.01 | 10.00 |
| K0003 | 39.74 | 41.40 | 71.61 | 31.87 | 30.21 | 0.00 | 0.01 | 10.00 |
| K0004 | 39.22 | 41.10 | 70.09 | 30.87 | 28.99 | 0.00 | 0.01 | 10.00 |
| K0005 | 16.77 | 18.35 | 42.09 | 25.32 | 23.74 | 0.00 | 0.01 | 8.35 |
| K0006 | 22.82 | 24.04 | 26.26 | 3.44 | 2.21 | 0.00 | 0.01 | 4.46 |
| K0007 | 33.58 | 95.94 | 35.59 | 2.01 | -60.35 | 0.00 | 0.01 | 6.83 |
| PID | AICdual | |||||||
| K0008 | 54.30 | 55.08 | 56.81 | 2.51 | 1.73 | 0.00 | 0.01 | 10.00 |
| K0009 | 47.31 | 48.57 | 53.31 | 6.01 | 4.75 | 0.00 | 0.01 | 10.00 |
| K0010 | 42.70 | 44.66 | 105.40 | 62.70 | 60.74 | 0.00 | 0.01 | 10.00 |
| K0011 | 48.99 | 49.99 | 51.02 | 2.03 | 1.03 | 0.00 | 0.01 | 10.00 |
| K0012 | 17.85 | 18.90 | 22.77 | 4.92 | 3.87 | 0.00 | 0.01 | 3.75 |
| K0013 | 33.48 | 35.36 | 47.64 | 14.17 | 12.28 | 0.00 | 0.01 | 10.00 |
| K0014 | 37.73 | 38.51 | 40.50 | 2.78 | 1.99 | 0.00 | 0.01 | 7.90 |
| K0015 | 34.12 | 36.12 | 44.67 | 10.55 | 8.55 | 0.00 | 0.01 | 9.12 |
| K0016 | 22.80 | 23.78 | 26.12 | 3.32 | 2.34 | 0.00 | 0.01 | 4.43 |
| K0017 | 38.00 | 39.92 | 60.99 | 22.99 | 21.07 | 0.00 | 0.01 | 10.00 |
| K0018 | 22.95 | 24.22 | 24.95 | 2.00 | 0.73 | 0.00 | 0.01 | 4.30 |
| K0019 | 19.70 | 20.68 | 21.73 | 2.03 | 1.06 | 0.00 | 0.01 | 3.52 |
| K0020 | 37.45 | 39.30 | 44.47 | 7.02 | 5.16 | 0.00 | 0.01 | 9.06 |
| K0021 | 35.65 | 37.65 | 107.22 | 71.56 | 69.56 | 0.00 | 0.01 | 10.00 |
| K0022 | 29.69 | 31.20 | 33.32 | 3.63 | 2.12 | 0.00 | 0.01 | 6.09 |
| K0023 | 27.40 | 29.31 | 63.83 | 36.43 | 34.52 | 0.00 | 0.01 | 10.00 |
| K0024 | 41.33 | 43.21 | 52.49 | 11.16 | 9.28 | 0.00 | 0.01 | 10.00 |
| K0025 | 12.13 | 12.48 | 21.07 | 8.95 | 8.59 | 0.00 | 0.01 | 3.39 |
| K0026 | 25.73 | 27.68 | 49.23 | 23.49 | 21.55 | 0.00 | 0.01 | 10.00 |
| K0027 | 36.33 | 38.37 | 45.97 | 9.64 | 7.60 | 0.00 | 0.01 | 9.53 |
| K0028 | 32.85 | 34.72 | 44.31 | 11.46 | 9.59 | 0.00 | 0.01 | 9.01 |
| K0029 | 69.70 | 70.14 | 96.52 | 26.82 | 26.38 | 0.00 | 0.01 | 10.00 |
| K0030 | 33.52 | 35.44 | 35.50 | 1.98 | 0.06 | 0.00 | 0.02 | 7.70 |
| K0031 | 24.75 | 26.71 | 57.11 | 32.37 | 30.40 | 0.00 | 0.01 | 10.00 |
| K0032 | 33.95 | 35.41 | 36.67 | 2.72 | 1.27 | 0.00 | 0.01 | 6.89 |
| PID | ||||||||
| K0033 | 25.76 | 27.19 | 28.07 | 2.31 | 0.88 | 0.00 | 0.01 | 4.85 |
| K0034 | 11.24 | 13.24 | 26.83 | 15.59 | 13.59 | 0.00 | 0.01 | 4.58 |
| K0035 | 76.05 | 77.57 | 115.10 | 39.05 | 37.53 | 0.00 | 0.01 | 10.00 |
| K0036 | 28.24 | 30.15 | 34.29 | 6.06 | 4.14 | 0.00 | 0.01 | 6.30 |
| K0037 | 23.64 | 25.48 | 28.41 | 4.77 | 2.94 | 0.00 | 0.01 | 4.93 |
| K0038 | 49.92 | 51.69 | 87.09 | 37.18 | 35.40 | 0.00 | 0.01 | 10.00 |
| K0039 | 36.70 | 38.67 | 48.49 | 11.79 | 9.81 | 0.00 | 0.01 | 10.00 |
| K0040 | 23.31 | 25.04 | 25.30 | 2.00 | 0.27 | 0.00 | 0.01 | 4.31 |
| K0041 | 26.64 | 28.05 | 42.30 | 15.67 | 14.26 | 0.00 | 0.01 | 8.41 |
| K0042 | 11.24 | 13.24 | 26.83 | 15.59 | 13.59 | 0.00 | 0.01 | 4.58 |
| K0043 | 30.16 | 31.29 | 35.25 | 5.09 | 3.96 | 0.00 | 0.01 | 6.53 |
| K0044 | 36.36 | 38.18 | 45.82 | 9.46 | 7.64 | 0.00 | 0.01 | 9.48 |
| K0045 | 25.73 | 27.68 | 49.23 | 23.49 | 21.55 | 0.00 | 0.01 | 10.00 |
| K0046 | 34.97 | 37.09 | 36.91 | 1.94 | -0.18 | 0.01 | 0.01 | 8.17 |
| K0047 | 39.42 | 40.23 | 41.63 | 2.21 | 1.40 | 0.00 | 0.01 | 8.22 |
| K0048 | 40.16 | 42.11 | 53.66 | 13.51 | 11.55 | 0.00 | 0.01 | 10.00 |
| K0049 | 33.53 | 35.47 | 50.23 | 16.69 | 14.76 | 0.00 | 0.01 | 10.00 |
| K0050 | 27.79 | 29.83 | 58.10 | 30.31 | 28.27 | 0.00 | 0.01 | 10.00 |
| K0051 | 40.14 | 41.86 | 49.32 | 9.19 | 7.46 | 0.00 | 0.01 | 10.00 |
| K0052 | 59.54 | 61.05 | 95.21 | 35.67 | 34.16 | 0.00 | 0.01 | 10.00 |
| K0053 | 33.05 | 34.86 | 46.16 | 13.11 | 11.30 | 0.00 | 0.01 | 9.59 |
| K0054 | 33.59 | 35.59 | 47.88 | 14.28 | 12.28 | 0.00 | 0.01 | 10.00 |
| K0055 | 50.37 | 52.12 | 95.47 | 45.09 | 43.34 | 0.00 | 0.01 | 10.00 |
| K0056 | 29.77 | 30.96 | 37.10 | 7.33 | 6.14 | 0.00 | 0.01 | 7.00 |
| K0057 | 17.36 | 19.31 | 65.08 | 47.72 | 45.77 | 0.00 | 0.01 | 10.00 |
| PID | ||||||||
| K0058 | 17.88 | 18.92 | 22.79 | 4.91 | 3.87 | 0.00 | 0.01 | 3.73 |
| K0059 | 45.15 | 46.37 | 62.98 | 17.83 | 16.61 | 0.00 | 0.01 | 10.00 |
| K0060 | 44.31 | 46.03 | 53.98 | 9.67 | 7.95 | 0.00 | 0.01 | 10.00 |
| K0061 | 33.45 | 35.40 | 40.19 | 6.75 | 4.80 | 0.00 | 0.01 | 7.82 |
| K0062 | 33.67 | 35.67 | 102.69 | 69.02 | 67.02 | 0.00 | 0.01 | 10.00 |
| K0063 | 43.98 | 44.95 | 46.17 | 2.19 | 1.21 | 0.00 | 0.01 | 9.60 |
| K0064 | 21.78 | 23.76 | 40.63 | 18.86 | 16.88 | 0.00 | 0.01 | 7.94 |
| K0065 | 29.42 | 31.38 | 68.02 | 38.61 | 36.64 | 0.00 | 0.01 | 10.00 |
| K0066 | 42.77 | 44.72 | 53.36 | 10.59 | 8.64 | 0.00 | 0.01 | 10.00 |
| K0067 | 23.62 | 25.20 | 29.76 | 6.14 | 4.56 | 0.00 | 0.01 | 5.23 |
| K0068 | 29.89 | 30.85 | 31.89 | 2.00 | 1.04 | 0.00 | 0.01 | 5.76 |
| K0069 | 31.19 | 33.13 | 52.90 | 21.71 | 19.77 | 0.00 | 0.01 | 10.00 |
| K0070 | 30.34 | 32.26 | 40.12 | 9.78 | 7.86 | 0.00 | 0.01 | 7.80 |
| K0071 | 105.80 | 107.03 | 143.50 | 37.70 | 36.47 | 0.00 | 0.01 | 10.00 |
| K0072 | 41.68 | 43.68 | 76.86 | 35.18 | 33.18 | 0.00 | 0.01 | 10.00 |
| K0073 | 23.71 | 25.64 | 47.96 | 24.26 | 22.32 | 0.00 | 0.01 | 10.00 |
| K0074 | 34.78 | 35.59 | 36.78 | 2.00 | 1.19 | 0.00 | 0.02 | 7.52 |
| K0075 | 21.87 | 23.82 | 57.52 | 35.65 | 33.70 | 0.00 | 0.01 | 10.00 |
| Comparison | N | Pearson r | p | 95% CI |
| ϑ vs. proportion delayed | 76 | -0.380 | 7.2×10-4 | [approx. -0.56, -0.17] |
| ϑ vs. SSRT | 101 | 0.070 | 0.487 | [approx. -0.12, 0.25] |
| Parameter | S1 (mean) | Note |
| ϑ | 0.0115 | primary outcome |
| k | 0.0060 | |
| ε | 0.0051 |
| alpha | k | p delayed |
| 0.01 | 0.001 | 0.439846 |
| 0.01 | 0.00127786 | 0.440833 |
| 0.01 | 0.00163294 | 0.439991 |
| 0.01 | 0.00208667 | 0.447554 |
| 0.01 | 0.00266649 | 0.418967 |
| 0.01 | 0.00340741 | 0.427309 |
| 0.01 | 0.00435421 | 0.399345 |
| 0.01 | 0.00556409 | 0.361362 |
| 0.01 | 0.00711015 | 0.353195 |
| 0.01 | 0.00908581 | 0.346185 |
| 0.01 | 0.0116104 | 0.333354 |
| 0.01 | 0.0148366 | 0.332723 |
| 0.01 | 0.0189591 | 0.327622 |
| 0.01 | 0.0242272 | 0.318327 |
| 0.01 | 0.0309591 | 0.269225 |
| Metric | Value | Count / Proportion |
| ϑ floor value | 0.010 | 71/76 (93.4%) |
| ε ceiling value | 10.0 | 39/76 (51.3%) |
| k minimum value | 0.0001 | 72/76 (94.7%) |
| k–ϑ Pearson r (95% CI) | 0.382 | [0.171, 0.559] |
References
- G. Ainslie. Picoeconomics: The strategic interaction of successive motivational states within the person. Cambridge University Press (1992). [↩]
- L. Green, J. Myerson. A discounting framework for choice with delayed and probabilistic rewards. Psychological Bulletin, 130(5), 769 (2004). [↩]
- S. M. McClure, D. I. Laibson, G. Loewenstein, J. D. Cohen. Separate neural systems value immediate and delayed monetary rewards. Science, 306(5695), 503–507 (2004). [↩]
- A. L. Odum. Delay discounting: I’m ak, you’re ak. Journal of the Experimental Analysis of Behavior, 96(3), 427–439 (2011). [↩]
- S. Weinsztok, S. Brassard, I. Balodis, L. E. Martin, M. Amlung. Delay discounting in established and proposed behavioral addictions: A systematic review and meta-analysis. Frontiers in Behavioral Neuroscience, 15, 786358 (2021). [↩]
- R. E. Weller, E. W. Cook III, K. B. Avsar, J. E. Cox. Obese women show greater delay discounting than healthy-weight women. Appetite, 51(3), 563–569 (2008). [↩]
- P. Ring, C. C. Probst, L. Neyse, S. Wolff, C. Kaernbach, T. van Eimeren, U. Schmidt. Discounting behavior in problem gambling. Journal of Gambling Studies, 2021, 1–15 (2021). [↩]
- M. Amlung, L. Vedelago, J. Acker, I. Balodis, J. MacKillop. Steep delay discounting and addictive behavior: A meta-analysis of continuous associations. Addiction, 112(1), 51–62 (2017). [↩]
- D. C. Lee, C. Stanger, A. J. Budney. A comparison of delay discounting in adolescents and adults in treatment for cannabis use disorders. Experimental and Clinical Psychopharmacology, 23(2), 130 (2015). [↩]
- T. Mena-Moreno, G. Testa, G. Mestre-Bach, R. Miranda-Olivos, R. Granero, F. Fernández-Aranda, J. M. Menchón, S. Jiménez-Murcia. Delay discounting in gambling disorder: Implications in treatment outcome. Journal of Clinical Medicine, 11(6), 1611 (2022). [↩]
- A. C. Exum, C. A. Sutton, J. S. Bellitti, R. Yi, T. L. Fazzino. Delay discounting and substance use treatment outcomes: A systematic review focused on treatment outcomes and discounting methodology. Journal of Substance Use and Addiction Treatment, 149, 209037 (2023). [↩]
- C. H. G. Patros, K. L. Sweeney, E. M. Mahone, S. H. Mostofsky, K. S. Rosch. Greater delay discounting among girls, but not boys, with ADHD correlates with cognitive control. Child Neuropsychology, 24(8), 1026–1046 (2018). [↩] [↩]
- G. J. Aranovich, S. M. McClure, S. Fryer, D. H. Mathalon. The effect of cognitive challenge on delay discounting. NeuroImage, 124(Part A), 733–739 (2016). [↩]
- M. Yu, T. Liu, F. Shangguan, J. Sui, J. Shi. The neurodevelopment of delay discounting for monetary rewards in pre-adolescent children. Scientific Reports, 11(1), 8337 (2021). [↩]
- P. Fernández-Martín, D. Tovar-Suárez, R. Rodríguez-Herrera, J. J. León, R. Cánovas, P. Flores. Behavioral and neurofunctional profiles of delay aversion in children with attention-deficit hyperactivity disorder. Translational Psychiatry, 15(1), 125 (2025). [↩]
- W. K. Bickel, R. Yi. Temporal discounting as a measure of executive function: Insights from the competing neuro-behavioral decision system hypothesis of addiction. In Neuroeconomics, 20, 289–309. Emerald Group Publishing Limited (2008). [↩]
- L. Green, J. Myerson. A discounting framework for choice with delayed and probabilistic rewards. Psychological Bulletin, 130(5), 769 (2004). [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩] [↩]
- F. Verbruggen, A.R. Aron, G.P.H. Band, C. Beste, P.G. Bissett, A.T. Brockett, J.W. Brown. A consensus guide to capturing the ability to inhibit actions and impulsive behaviors in the stop-signal task. eLife, 8, e46323 (2019). [↩] [↩] [↩]
- P.G. Bissett, I.W. Eisenberg, S. Shim, J.A.H. Rios, H.M. Jones, M.P. Hagan, A.Z. Enkavi, J.K. Li, J.A. Mumford, D.P. MacKinnon, L.A. Marsch, R.A. Poldrack. Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation. OpenNeuro, 2024. Dataset accession: ds004636. [↩] [↩] [↩]
- P.G. Bissett, I.W. Eisenberg, S. Shim, J.A.H. Rios, H.M. Jones, M.P. Hagan, A.Z. Enkavi, J.K. Li, J.A. Mumford, D.P. MacKinnon, L.A. Marsch, R.A. Poldrack. Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation. Scientific Data, 2024. Data descriptor for OpenNeuro ds004636. [↩] [↩] [↩]
- K. N. Kirby, N. M. Petry, W.K. Bickel. Heroin addicts have higher discount rates for delayed rewards than non-drug-using controls. Journal of Experimental Psychology: General, 128(1), 78–87 (1999). [↩] [↩]
- T. L. McKerchar, L. Green, J. Myerson. On the scaling interpretation of exponents in hyperboloid models of delay and probability discounting. Behavioural Processes, 84(1), 440–444 (2010). [↩] [↩] [↩] [↩]
- S. Frederick, G. Loewenstein, T. O’Donoghue. Time discounting and time preference: A critical review. Journal of Economic Literature, 40(2), 351–401 (2002). [↩] [↩] [↩] [↩]
- S. M. McClure, D. I. Laibson, G. Loewenstein, J. D. Cohen. Separate neural systems value immediate and delayed monetary rewards. Science, 306(5695), 503–507 (2004). [↩] [↩] [↩]
- W. K. Bickel, R. Yi. Temporal discounting as a measure of executive function: Insights from the competing neuro-behavioral decision system hypothesis of addiction. In Neuroeconomics, 20, 289–309. Emerald Group Publishing Limited (2008). [↩] [↩] [↩]
- Z. Kurth-Nelson, W. K. Bickel, A. D. Redish. A theoretical account of cognitive effects in delay discounting. European Journal of Neuroscience, 35(7), 1052–1064 (2012). [↩] [↩] [↩] [↩]
- T. V. Wiecki, M. J. Frank. A computational model of inhibitory control in frontal cortex and basal ganglia. Psychological Review, 120(2), 329 (2013). [↩] [↩] [↩] [↩]
- F. Verbruggen, A. R. Aron, G. P. H. Band, C. Beste, P. G. Bissett, A. T. Brockett, J. W. Brown. A consensus guide to capturing the ability to inhibit actions and impulsive behaviors in the stop-signal task. eLife, 8, e46323 (2019). [↩] [↩] [↩] [↩] [↩]
- P. G. Bissett, I. W. Eisenberg, S. Shim, J. A. H. Rios, H. M. Jones, M. P. Hagan, A. Z. Enkavi, J. K. Li, J. A. Mumford, D. P. MacKinnon, L. A. Marsch, R. A. Poldrack. Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation. OpenNeuro, 2024. Dataset accession: ds004636. [↩] [↩] [↩] [↩]
- P. G. Bissett, I. W. Eisenberg, S. Shim, J. A. H. Rios, H. M. Jones, M. P. Hagan, A. Z. Enkavi, J. K. Li, J. A. Mumford, D. P. MacKinnon, L. A. Marsch, R. A. Poldrack. Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation. Scientific Data, 2024. Data descriptor for OpenNeuro ds004636. [↩] [↩] [↩]
- Z. Song, Y. Wang, P. Qian, S. Song, F. Coenen, Z. Jiang, J. Su. From deterministic to stochastic: An interpretable stochastic model-free reinforcement learning framework for portfolio optimization. Applied Intelligence, 53(12), 15188–15203 (2023). [↩] [↩] [↩]
- D. Silver, G. Lever, N. Heess, T. Degris, D. Wierstra, M. Riedmiller. Deterministic policy gradient algorithms. In International Conference on Machine Learning, 387–395. PMLR (2014). [↩] [↩] [↩]
- K. N. Kirby, N. M. Petry, W. K. Bickel. Heroin addicts have higher discount rates for delayed rewards than non-drug-using controls. Journal of Experimental Psychology: General, 128(1), 78–87 (1999). [↩]
- P. G. Bissett, I. W. Eisenberg, S. Shim, J. A. H. Rios, H. M. Jones, M. P. H. Hagan, A. Z. Enkavi, J. K. Li, J. A. Mumford, D. P. MacKinnon, L. A. Marsch, R. A. Poldrack. Cognitive tasks, anatomical MRI, and functional MRI data evaluating the construct of self-regulation. Scientific Data, 2024. Data descriptor for OpenNeuro ds004636. [↩]