Analysis of Mathematical Elements and Physical Principles in K-Pop Dance

November 5, 2025

Abstract

This paper aims to explore the mathematical elements and physical principles in K-Pop dance popular among global youth, revealing their aesthetic and logical connections in dance art. Firstly, using mathematical modeling, it analyzed the mathematical elements, such like trigonometric functions, in K-Pop dance. Taking the squatting wave in LE SSERAFIM’s “ANTIFRAGILE” as a specific case, the mathematical model was described by sine function. Through data collection and verification of model fitting degree, it was proved that this motion followed the law of sine wave propagation. Then, through experimental observation and calculation, it explored physical principles, such like angular momentum conservation, in K-Pop dance. Taking the “End Spin” of BLACKPINK’s Lisa in “How You Like That” for example, it analyzed the influence of body posture on the rotation speed. By calculating Lisa’s moment of inertia and angular velocity at different rotation stages, this motion was verified conforming to the angular momentum conservation basically. This research provides a new perspective and idea for the interdisciplinary study of dance art.

Keywords: K-Pop Dance, Trigonometric Functions, Angular Momentum Conservation, Mathematical Modeling, Experimental Observation

Introduction

K-Pop dance is one of the key parts in Korean music culture. Its core elements consist of synchronization, simple and memorable ” Point Dance “, the integration of diverse elements such as hip-hop, jazz, street dance and modern dance, as well as a choreographic style that emphasizes both technicality and performance. As a form of dance that is popular among global youth nowadays, the dance club I founded always presents K-Pop dance programs at the school’s annual art festival.

In recent years, the research on the mathematical and physical aspects of K-pop dance has emerged as a new area in the intersection of art and science. Researchers use mathematical tools like mathematical modeling, graph and group theory to analyze group choreography’s formation changes, motion synchrony, and rhythmic patterns¹. Mathematical modeling transforms real-world problems into mathematical ones through abstraction and computation, achieving quantitative analysis, optimized decision-making, and scientific prediction, serving as a cornerstone of interdisciplinary research. Mathematical modeling is widely applied in scenarios such as epidemic prediction and drug development, financial analysis and market forecasting, film and television special effects and scene rendering, pollution control and urban planning. Combined with big data and AI technologies, it promotes interdisciplinary innovation and scientific progress. Researchers also apply biomechanics and sports physics to examine energy transfer and body dynamics in K-Pop’s symbolic motions systematically². This research offers data-driven insights for choreography and unique cultural samples for human sports science. It would further uncover the mathematical and physical essence behind artistic expression, fostering deeper integration and innovation between art and science.

There are many mathematical elements in K-Pop dance which are familiar to high school students. The geometry and symmetry in the formation design and movement trajectories, the rhythm and periodicity via the beat count and the repetition and variation of movements, the proportion and fractals through motion amplitude control and fractal nesting, all of them reveal the mathematical beauty hidden in K-Pop dance.

The physical principles contained in K-Pop dance we are familiar with mainly include mechanics, kinematics and fluid dynamics. The rapid pauses and variable-speed rotations in fixed-point actions utilize momentum and angular momentum conservation. Member interactions make use of elastic collisions and energy transfer. Multi-axis rotation in complex choreography takes advantage of the Coriolis Force effect. These physics principles blend with artistry for unique visual impact.

Therefore, as high school students, regarding some symbolic motions imitated frequently by our dance club in K-Pop dance, this paper attempts to find and verify the mathematical elements we have learned through experimental observation and mathematical modeling, to analyze and verify the physical principles we are already familiar with through experimental observation and computational verification, to explore the profound connections among mathematics, physics and dance, and to reveal the common aesthetic logic among them.

Preliminary Concepts

Trigonometric functions

Trigonometric functions are a set of functions that describe the relationship between angles and side lengths, including sine, cosine, and tangent, with the universality of periodicity and proportion as their cores. The sine wave starts from the middle zero point, rises first and then falls, forming a smooth oscillation. The cosine wave starts from the highest point, descends first and then rises, presenting symmetrical ups and downs. The waveforms of the two are exactly the same, except for the different starting positions. The sine wave is equivalent to the cosine wave shifted to the left by one quarter of a cycle. Trigonometric functions all have fixed amplitudes, periods and phases. They are widely used to describe sound waves, light waves and other periodic phenomena with fixed changing patterns. The standard sine function is: $y(x)=A \sin⁡(\omega x+\Delta \varphi)+y_0$ .

Conservation of Angular Momentum

The conservation of angular momentum, along with the conservation of momentum and the conservation of energy, are known as three major conservation theorems in classical physics. The angular momentum $L$ of a physical system is: $L=I\times \omega$ . Here, $𝐼$ is the moment of inertia, depending on the mass distribution of rotating object and the rotating axis. During the dance, the moment of inertia of a dancer can be described as: $I=\sum m_i r_i^2$ , $m_i$ , is the mass of a rotating body part, such as trunk, arms or legs $r_i$ , is the radius from the center of body part to the axis. Total $𝐼$ of a dancer sums all rotating parts, and is closely related to the body shape when motions change. $\omega$ is the angular velocity vector. Without external torque, the total angular momentum of the system is conserved, that is, $\Delta L=0$ .

Review of Mathematical & Physical Aspects in K-Pop Dance

Elements of Trigonometric Functions

The dance motions and formations in K-Pop dance are renowned for its high degree of synchronization, smoothness and visual impact. The periodicity, volatility and symmetry characteristics of trigonometric functions can effectively and abstractly describe many symbolic K-Pop motions. Unveiling the hidden trigonometric elements in K-Pop dance not only integrates visual aesthetics with mathematical elements perfectly, but also enhances the dance’s transmissibility, memorable points and emotional expression significantly.

The Sine Function in Wavy Motions

In LE SSERAFIM’s “ANTIFRAGILE”, squatting waves are formed as five members squat sequentially, creating fluid motion. In IZ*ONE’s “Panorama”, a circular human radial wave with 12 members makes the formation contracting and expanding like breathing, mimicking 3D depth on a 2D stage.

The Cosine Function in Periodic Oscillations

In NewJeans’ “Hype Boy”, the arm swing alternates between the left and right hands to draw arcs, using cosine function for a wonderful balance between mechanical feeling and agility. In BTS’s “Butter”, the shoulder rolls form an “∞”, one of the most recognizable shoulder motions in the history of K-Pop, is to stimulate sensory uncertainty through mathematical certainty.

Applications of Composite Trigonometric Functions

In Aespa’s “Next Level”, the snake-like motion superimpose the high-frequency jitter on the low-frequency waves. Through the precise design of the composite function, the visual effect of the snake-shaped trajectory is finally formed. It constructs supernatural movements through mathematics, maintaining the foundation of human actions while injecting the unique digital beauty of AI with harmonic components.

The Phenomenon of Angular Momentum

K-Pop dance combines angular momentum conservation, which is a scientific principle, with aesthetics to create dynamic visual effects, enhancing performance strength and fluidity. This blend of science and art is a key reason it captivates audiences.

Conservation of Angular Momentum in Rotational Motion

For example, when BLACKPINK’s Lisa spins at the end of “How You Like That”, pulling her arms and body inward reduces her moment of inertia, making her spin faster. Conversely, extending her arms slows the spin. Another case, in BTS’s “ON” or NCT’s routines, dancers who synchronize by tucking inward and spinning together amplify visual impact and showcase coordinated “Collective Angular Momentum”.

Angular Momentum Control in Leaping in the Air

While airborne, dancers’ total angular momentum stays constant, so they adjust their limbs to stay balanced. For example, in EXO’s “Love Shot” or TWICE’s jumps, dancers control their spin speed by extending or retracting arms and legs to land steadily. In BTS’s “Dynamite”, the tilted dance steps maintain a total angular momentum of zero by rotating the upper and lower body in opposite directions.

Angular Momentum Transfer in Floor Motions

When a dancer touches the floor, friction, which is an external force, can alter the angular momentum. In BTS’s J-Hope, dancer uses a hand to push the floor during floor spins, creating torque to start rotating, while pulling his other hand in to speed the spin up. In SEVENTEEN’s “HOME; RUN”, sliding steps are paired with spins, the sliding reduces friction, letting the spin last longer.

“Angular Momentum Illusion” by Group Choreography

The choreography’s visual design simulates angular momentum transfer through formation shifts. In GFRIEND’s “Time for the Moon Night”, dancers rotate sequentially, creating “momentum waves”. In AESPA’s “Next Level”, the central dancer spins while outer members move oppositely to keep the group’s balance dynamic.

Methods

All the data accuracy of the conclusions in this research was only based on the calculation process itself. Except for the corrected data mentioned, no other related error factors had been taken into account.

Mathematical Modeling for Familiar Case

During dance club rehearsals, we often imitate K-Pop’s wavy moves. Therefore, we analyzed the squatting wave move in LE SSERAFIM’s “ANTIFRAGILE”, which appears in the chorus. As shown in Figures 1 to 5, five dancers stand in a row, linking their arms in sequence with one arm each. Then the first dancer raises her right arm horizontally forward. In time with the music, each dancer in turn bends their left leg, while slightly squatting and standing up with their right leg – overlapping at the beginning and end. While squatting, their upper bodies twist in unison to form a wavelike motion, creating a seamless “human wave”. The team’s synchronized movement amplitude and rhythm produce a cohesive, energetic visual effect.

Data Collection

We selected a 4K MV from Bilibili (2024-12-8), that was shot from a fixed camera with no angle distortion, used the open-source software Tracker to extract motion data, set the stage’s left-right direction as the X-axis with the direction to the right; and the video’s top as the Y-axis starting height with the direction downward. The waist of the members, as the pelvis’s most prominent part, were marked manually as the observation point to minimize head-shaking effects, with data in pixels (px). Starting with the first member Karina squatting from the half-squat position, we measured at 0.1-second intervals over a 5-second period (MV time: 0:40–0:45). After the measurement, the data of each member’s time (t) and vertical position (y) were obtained as shown in Table 1 (omitted).

Time (s)	Karina (px)	Sakura (px)	Chaewon (px)	Yunjin (px)	Eunchae (px)
0.0	1400	1209	1201	1200	1201
0.1	1440	1225	1201	1200	1201
0.2	1482	1250	1201	1200	1201
…	…	…	…	…	…
0.6	1589	1401	1208	1200	1201
0.7	1595	1439	1224	1201	1200
0.8	1594	1482	1249	1200	1200
0.9	1588	1517	1280	1200	1201
…	…	…	…	…	…
1.2	1518	1588	1401	1209	1201
…	…	…	…	…	…
1.8	1282	1516	1589	1395	1210
…	…	…	…	…	…
3.0	1400	1209	1281	1513	1590
…	…	…	…	…	…

Table 1| Data of Squat Waves in “ANTIFRAGILE”

Table 1 shows that each member starts the squatting action successively from the semi-squatting position, which is 1400px approximately, with an interval of approximately 0.6 seconds. The height difference between full standing and full squatting is about 400px, that is, the amplitude is about 200px. Karina takes 0.7–0.8 seconds to rise from a full squat, while others maintain about 0.6-second intervals. Each member completes a full squat-stand cycle in about 3 seconds, and the 5-member wave takes about 3 seconds to complete an overall form.

Mathematical Modeling

We analyzed LE SSERAFIM’s “ANTIFRAGILE” wave dance motion’s mathematical modeling from biomechanics and mathematical simplicity.

The analysis of biomechanics is based on the natural trajectory of human joint motion. The knee’s flexion angle θ(t) during squats follows a cosine function, which is derivative of sine, resulting in vertical displacement y(t) with a sine characteristic³. Meanwhile, the wave dance’s repetitive undulations and changes align with the sine function’s periodic nature.

The analysis of mathematical simplicity includes the principle of minimizing parameters in mathematical modeling and the error robustness of sine functions. As a fundamental Fourier series component, the sine function requires fewer parameters than other periodic functions like square, triangular, or sawtooth waves. Only three parameters, namely amplitude A, angular frequency ω and phase difference Δϕ, are needed to describe the action fully. Meanwhile, even if there is a ±10% execution deviations by team members, the sine wave’s smoothness preserves more than 80% of the visual effect, whereas linear or zigzag models would show noticeable breaks at 5% deviations.

Therefore, the sine wave is the most appropriate function to describe the wavy motions in a team dance. The standard sine function was adapted into a mathematical model for tracking a team member’s body height changes over time in the “ANTIFRAGILE” wave dance, as shown in Equation 1.

(1) $\begin{equation*}y_n(t) = A \sin \left( \frac{2\pi}{T}t - \frac{2\pi(n-1)}{N} \right) + y_0\end{equation*}$

Here, A is the amplitude, and T is the period to form the human wave. Compared with the standard sine function, ω=2π/T. From the collected data, the start time delay among each dancer is about 0.6 seconds, which is T/5. In terms of phase value, it is 2π/N, where N=5 is the number of dancers forming the wave. n is the sequential ID of dancers (n=1-5 in “ANTIFRAGILE”), n-1 achieves an alternating difference. y₀ is the initial position for each dancer, the semi-squatting position in the dance. Based on Table 1’s analysis, it can be concretized as Equation 2. The curves were shown in Figure 6, in which all dancers started from the initial position y₀ and shown one cycle. It could be seen that the curves representing all dancers were basically in correspondence with their motions shown in Figures 1 to 5.

(2) $\begin{equation*}y_n(t) = 200 \sin \left( \frac{2\pi}{3}t - \frac{2\pi(n-1)}{5} \right) + 1400\end{equation*}$

Figure 6 | Graph of Position Curves for Each Dancer

Verification of Model Fit

(i) Determination Coefficient (R²) As the core indicator of fit in regression analysis, determination coefficient is defined as Equation 3

(3) $\begin{equation*} R^2 = 1 - \frac{SSE}{SST} = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} \end{equation*}$

Here, 𝑛 is the number of observation points, y_i is the measured value at point i, ŷᵢ is the model’s calculated value. SSE is the sum of squared residuals, representing unexplained model variation. ȳ is the mean of all measured values, and SST is the total sum of squared differences between measured values and the mean, indicating the observed data’s total variation

For small datasets, Excel’s planning and solving features can substitute Python’s curve_fit for calculating the fit of simple models. In this paper, Excel was used as data processing tool, importing the observed data firstly, using the DEVSQ function to calculate the total sum of squared deviations (SST) and the SUMSQ function for the sum of squared residuals (SSE).

Take Karina as an example. As the first member to initiate the wave, 𝑛=1, and her model is shown as Equation 4.

(4) $\begin{equation*}y_1(t) = 200 \sin \left( \frac{2\pi}{3}t \right) + 1400\end{equation*}$

I inserted a column (C) to the right of Karina, entered Equation 4 in cell C2, replaced t with A2, and dragged to fill all time points for Karina’s model values. Then I calculated SST with DEVSQ(B2:B31) and SSE with SUMSQ(B2:B31-C2:C31), then the determination coefficient R² was obtained. The same were applied to other members. Starting from the half-squat position (≈1400px), the squatting count was continuously counted for 30 measurement values, the determination coefficients for other members were obtained.

(ii) Phase Difference (Δϕ)

In Tracker software, I manually marked the start time (t₁=0) when the first member began squatting from the 1400px semi-squat position. Then, I marked each subsequent member’s squat start time (tᵢ) and calculated the time difference: ∆tᵢ = tᵢ – tᵢ₋₁. The phase difference is: ∆ϕᵢ = (2π/3) × ∆tᵢ.

(iii) Root Mean Square Error (RMSE)

The calculation expression of RMSE is shown as Equation 5, taking px as the unit. Similarly, Excel was used as a calculation tool.

(5) $\begin{equation*}\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}\end{equation*}$

The relevant data for the verification of the model fit degree are shown in Table 2.

Member	R²	Δφ	RMSE/px
Karina	0.982	0⁰	12.1
Sakura	0.976	73.6⁰	14.3
Chaewon	0.979	72.9⁰	13.6
Yunjin	0.973	74.5⁰	15.0
Eunchae	0.985	72.2⁰	11.7
Team average	0.979	73.3⁰	13.3

Table 2 |Verification Data of Model Fitting

Analysis of Angular Momentum Conservation for Familiar Case

The single-person rotation is the K-Pop dance motion our club imitates mostly. At the end of BLACKPINK’s “How You Like That”, approximately 3 minutes and 20 seconds into the dance, Lisa does a rapid Pirouette, a signature motion known as the “End Spin”. It lasts 2-3 seconds with 4-6 rotations. The dancer keeps arms tight to the body and legs upright or slightly bent. This “End Spin” follows an “acceleration – stabilization – deceleration” process in three stages, which is start-up, acceleration, and deceleration, as shown in Table 3.

Stage	time duration(s)	Body Posture	Change in Angular Velocity
start-up	0.0-0.5	Arms are half-spread and push the floor with one foot.	Rise rapidly from 0
acceleration	0.5-1.5	Arms are tightened and the core is stable.	Increase rapidly and reach the peak
deceleration	1.5-3.0	Arms are fully extend and adjust the balance.	Decrease gradually until it stops

Table 3 | Description of Three Stages of “End Spin”

During the start-up, Lisa half-spreads her arms to increase the moment of inertia and pushes the floor with one foot for external torque, creating initial angular momentum. In acceleration, she tightens her arms to lower the moment of inertia, boosting rotation speed to its max. During deceleration, she spreads her arms to raise the moment of inertia, slowing the rotation. Friction between her feet and the floor generates a reverse torque, gradually depleting the angular momentum until she stops rotating.

Moment of Inertia of Lisa’s Body

Based on the information from BLACKPINK’s agency (YG Entertainment) and Lisa’s personal social media, her basic physical stats are: height 166cm, weight 45kg (arms make up about 15% of that), arm span 167cm, and each arm is 38cm long.

The human body’s moment of inertia depends on the mass distribution and the rotation axis’s position. Since the body is a non-completely rigid body, its moment of inertia changes with posture. In biomechanics and sports science, the Segment Model is often used for calculations⁴. For Lisa’s rotation, we divided it into two parts: the trunk, including head and legs, and the arms. The trunk rotates like a cylinder around a vertical axis, while the arms, according to the parallel axis principle, rotate like slender rods around the shoulder joint. These were labeled as Part 1 and Part 2. The body’s moment of inertia is given by Equation 6.

(6) $\begin{equation*}I = I_1 + I_2 = \frac{1}{2} m_1 r^2 + \frac{1}{12} m_2 L^2 + m_2 d^2\end{equation*}$

Here, m₁ and m₂ represent the masses of two body parts. The trunk’s radius (r) is about 12cm, and L is the length of each arm. Lisa’s rotation has three stages, with three different body posture respectively. When her arm is half-extended, $d=r + L/4$ ; when tightened, $d=0$ ; when fully extended, $d=r + L/2$ .

The actual data of moment of inertia would be slightly higher than calculations due to factors like head offset, legs not fully together to increase distance from the rotation axis, and loose clothing to increase effective radius. The research result from S. Kim and J. Park in 2021⁵ provides corrected data which are shown in Table 4.

Stage	Body Posture	Legs not Together	Loose Clothing	Head Offset
start-up	Arms half-spread, legs slightly apart.	+0.2kg.m²	+0.15 kg.m²	+0.05 kg.m²
acceleration	Arms tightened, legs keep together.	0	+0.05kg.m²	+0.05 kg.m²
deceleration	Arms fully-spread, legs slightly apart.	+0.2kg.m²	+0.3 kg.m²	+0.05 kg.m²

Table 4 | Corrected Data of Moment of Inertia

Lisa’s Rotational Angular Velocity

The frame-by-frame analysis for videos was adopted⁶. Three 4K/60fps MV clips of BLACKPINK’s “How You Like That” released at different times on YouTube were chosen, and the video editing software Adobe Premiere was used. Lisa’s nose tip was marked as a reference point, and the number of rotations and the time were counted frame by frame.

Rotational angular velocity , ∆θ is the angle rotated by Lisa in k frames, and ∆t=k/60 is the corresponding time length.

I picked three key moments as the angular velocity marking points for three stages in sequence. They were the end of the start-up (0.5s), arms were fully tightened during acceleration, and arms were fully extended during deceleration. I measured and calculated angular velocities from three videos, then averaged them for each of three points. It gave Lisa’s angular velocities at three key moments during her “End Spin”.

Conclusion

By analyzing how trigonometric functions and angular momentum conservation are involved in K-Pop dance motions, this study reveals how mathematical elements and physical principles influence dance’s visual appeal and dynamic balance. It shows that K-Pop dance blends artistic expression with scientific logic through mathematical and physical principles implicitly, offering a fresh perspective on dance’s interdisciplinary nature.

Mathematical Modeling

The model fitting verification results of the squat wave motion in LE SSERAFIM’s “ANTIFRAGILE” are shown in Figure 7, phase difference is shown in Figure 8, which 1-5 in figures are Karina to Eunchae orderly. In the verification of mathematical modeling, the judgment criteria for model qualification vary depending on different application scenarios. In the entertainment scenario, the qualified standards for the core indicators such as the coefficient of determination (R²) and the root mean square error (RMSE) are usually more flexible than those in traditional science or engineering fields. A comprehensive judgment needs to be made based on business goals and data characteristics. Regarding the modeling of dance movements, no public research has shown a universally recognized “qualified” standard. Considering the Korean characteristics of K-pop, this research referred to the research result from J. Kim in 2023⁷, used the entertainment standards of SM Company in South Korea as the comparison value for judgment.

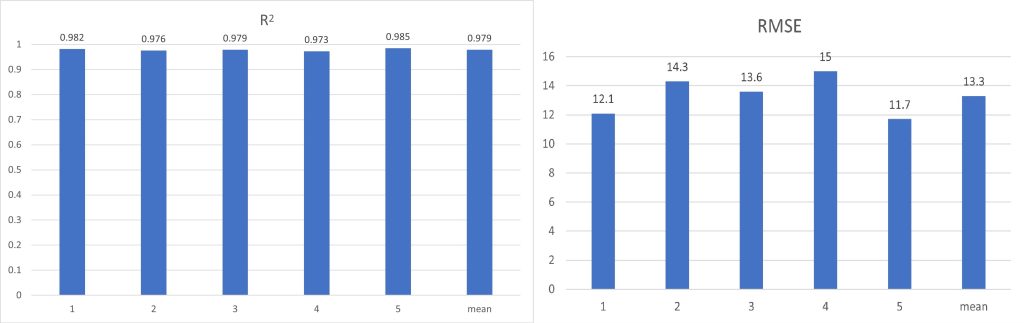
Figure 7| Model fitting verification results

Figure 8 | Phase Difference between each member

It can be concluded from Table 2, Figure 7 and 8 that the team’s average determination coefficient (R²) is 0.979, exceeding SM Entertainment’s standard (≥0.95). The average phase difference (Δφ) is 73.3⁰, with a 1.8% error from the theoretical 72⁰, which is lower than SM’s 5% limit. The root mean square error (RMSE) is 13.3, meeting SM’s ≤15px standard, but the first dancer needs to improve (≤ 10px). The error in this verification would arise from the local trajectory deviation caused by the fluttering of the clothing, the initial frame fitting deviation caused by the nonlinearity of the acceleration during squatting start and stop, as well as the measurement noise, etc.

The verification shows that the squatting wave motions of the five dancers in “ANTIFRAGILE” follow the law of sine wave propagation, aligning with National Geographic’s analysis (2023)⁸. The 72⁰-phase difference is crucial for visual smoothness, achieved by creating a “human waveform” through phase differences.

Angular Momentum Conservation

Those data of Lisa’s moment of inertia, angular velocity at the marking points and the corresponding angular momentum for the three stages of the “End Spin” are shown in Table 5 and Figure 9.

Stage	Moment of Inertia (kg.m²)	Angular Velocity (rad/s)	Angular Momentum (kg.m²/s)
start-up	1.2	6.25	7.5
acceleration	0.6	13	7.8
deceleration	1.8	4.15	7.47

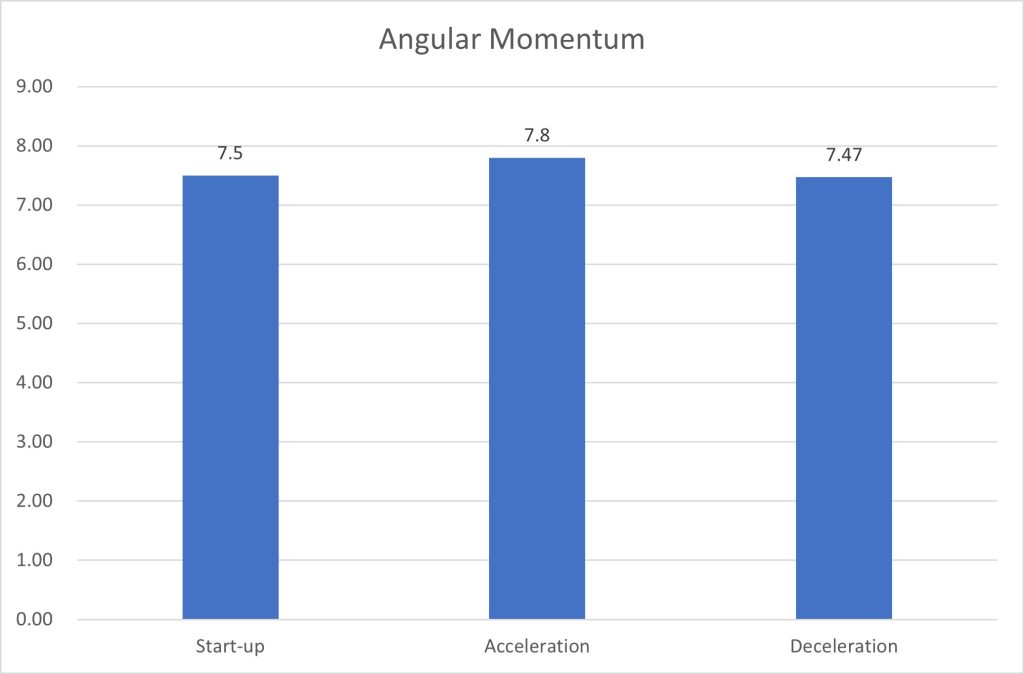
Table 4 | Angular Momentum of Three Stages of “End Spin”

Figure 9: Angular Momentum of Three Stages of “End Spin”

The moment of inertia during deceleration matches the data from dancers with a similar body type to Lisa, as reported by Wilmerding and Krasnow⁹. Comparing angular momentum across three stages shows that, ignoring the body’s flexibility and external forces, Lisa’s “End Spin” follows the law of angular momentum conservation generally. By adjusting her posture, Lisa controls her rotation speed precisely. Blending physics principles with dance expression, “End Spin” has become one of the classic moments of K-Pop.

Limitations

Due to the limited knowledge of mathematics and physics I mastered, in this research, a relatively simple sine function was adopted for the mathematical modeling of the squatting wave motion, and the calculation of the moment of inertia for Lisa in “End Spin” was also relatively not complicated. With the accumulating of knowledge, I would use more complex mathematical models and more detailed and precise calculations to better analyze the mathematical elements and physical principles contained in K-Pop dance.

Meanwhile, with the accumulating of knowledge in fields of biomechanics and advanced physics, I could apply knowledge such as biomechanics and human kinematics, more precise and reasonable methods for obtaining dance motion data, as well as quantitative assessments of error sources, to better modeling and analysis motions in K-Pop dance. The surface nature and shortcomings of this research would be further improved by going beyond basic mathematics and physics.

Closing Thought

For high school students passionate about dance, practicing it not only boosts their enthusiasm for mathematics and physics but also deepens their understanding of these subjects. Conversely, mathematics and physics enhance their grasp of dance motions, increasing their interest and motivation to dance.

X. Liu. Thought, Technique, Emotion: The Three Crucial Aspects of Choreography. Highlights in Art and Design. 8(1), 41-43 (2024). [↩]
H. Li. Technical analysis and simulation of dance movements based on biomechanical theory. Molecular & Cellular Biomechanics. 22(5), 1-13 (2025). [↩]
T. Tang, J. Zheng, L. Wang, F. Yang. Biomechanical analysis of martial arts movements: Implications for performance and injury prevention. Molecular & Cellular Biomechanics. 21(4), 1-21 (2024). [↩]
P. D. Leva. Estimation of Human Body Segment Parameters: A Comparative Study. Journal of Biomechanics. 29(9), 1223-1230 (1996). [↩]
S. Kim, J. Park. Kinematic Analysis of Pirouette in Ballet and K-pop Dance: A Comparative Study. Journal of Dance Medicine & Science. 25(3), 145-156 (2021). [↩]
J. Kim, S. Park. Kinematic Analysis of Rotational Movements in K-pop Dance Performances. International Conference on Entertainment Computing (Springer). 231-242 (2020). [↩]
J. Kim. Quantitative Evaluation of Group Dance Synchronization in K-Pop. Journal of Human Movement Science. 12(3), 45-67 (2023). [↩]
S. Kim, K. Lee. The Science Behind K-Pop’s Perfect Synchronization. National Geographic. 03, 71-81 (2023). [↩]
M. V. Wilmerding, D. H. Krasnow. The Physics of Dance: A Biomechanical Analysis of Pirouettes. Journal of Dance Medicine & Science. 17(2), 63-71 (2013). [↩]

Analysis of Mathematical Elements and Physical Principles in K-Pop Dance

Abstract

Introduction